ЛЕКЦИЯ 5 1 страница

Контрольные задания

Имеются данные (табл. 27) о продажах минимаркетом 3-х видов однородных товаров (A, B и C).

Таблица 27. Варианты выполнения контрольного задания

Вид товара	Цена за единицу товара, руб.	Объем продаж, тыс. штук		Вид товара	Цена за единицу товара, руб.	Объем продаж, тыс. штук
1 квартал	2 квартал	1 квартал	2 квартал		1 квартал	2 квартал	1 квартал	2 квартал
1 вариант		6 вариант
А						А
В						В
С						С
2 вариант		7 вариант
А						А
В						В
С						С
3 вариант		8 вариант
А						А
В						В
С						С
4 вариант		9 вариант
А						А
В						В
С						С
5 вариант		10 вариант
А						А
В						В
С						С

Рассчитать всевозможные индексы, выполнить факторный анализ выручки от продажи товаров. По итогам расчетов сделать аргументированные выводы.

Приложения – статистические таблицы

Приложение 1. Значения интеграла Лапласа

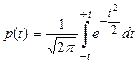
t	Сотые доли
0,00	0,0000	0,0080	0,0160	0,0239	0,0319	0,0399	0,0478	0,0558	0,0638	0,0717
0,10	0,0797	0,0876	0,0955	0,1034	0,1113	0,1192	0,1271	0,1350	0,1428	0,1507
0,20	0,1585	0,1663	0,1741	0,1819	0,1897	0,1974	0,2051	0,2128	0,2205	0,2282
0,30	0,2358	0,2434	0,2510	0,2586	0,2661	0,2737	0,2812	0,2886	0,2961	0,3035
0,40	0,3108	0,3182	0,3255	0,3328	0,3401	0,3473	0,3545	0,3616	0,3688	0,3759
0,50	0,3829	0,3899	0,3969	0,4039	0,4108	0,4177	0,4245	0,4313	0,4381	0,4448
0,60	0,4515	0,4581	0,4647	0,4713	0,4778	0,4843	0,4907	0,4971	0,5035	0,5098
0,70	0,5161	0,5223	0,5285	0,5346	0,5407	0,5467	0,5527	0,5587	0,5646	0,5705
0,80	0,5763	0,5821	0,5878	0,5935	0,5991	0,6047	0,6102	0,6157	0,6211	0,6265
0,90	0,6319	0,6372	0,6424	0,6476	0,6528	0,6579	0,6629	0,6680	0,6729	0,6778
1,00	0,6827	0,6875	0,6923	0,6970	0,7017	0,7063	0,7109	0,7154	0,7199	0,7243
1,10	0,7287	0,7330	0,7373	0,7415	0,7457	0,7499	0,7540	0,7580	0,7620	0,7660
1,20	0,7699	0,7737	0,7775	0,7813	0,7850	0,7887	0,7923	0,7959	0,7995	0,8029
1,30	0,8064	0,8098	0,8132	0,8165	0,8198	0,8230	0,8262	0,8293	0,8324	0,8355
1,40	0,8385	0,8415	0,8444	0,8473	0,8501	0,8529	0,8557	0,8584	0,8611	0,8638
1,50	0,8664	0,8690	0,8715	0,8740	0,8764	0,8789	0,8812	0,8836	0,8859	0,8882
1,60	0,8904	0,8926	0,8948	0,8969	0,8990	0,9011	0,9031	0,9051	0,9070	0,9090
1,70	0,9109	0,9127	0,9146	0,9164	0,9181	0,9199	0,9216	0,9233	0,9249	0,9265
1,80	0,9281	0,9297	0,9312	0,9328	0,9342	0,9357	0,9371	0,9385	0,9399	0,9412
1,90	0,9426	0,9439	0,9451	0,9464	0,9476	0,9488	0,9500	0,9512	0,9523	0,9534
2,00	0,9545	0,9556	0,9566	0,9576	0,9586	0,9596	0,9606	0,9615	0,9625	0,9634
2,10	0,9643	0,9651	0,9660	0,9668	0,9676	0,9684	0,9692	0,9700	0,9707	0,9715
2,20	0,9722	0,9729	0,9736	0,9743	0,9749	0,9756	0,9762	0,9768	0,9774	0,9780
2,30	0,9786	0,9791	0,9797	0,9802	0,9807	0,9812	0,9817	0,9822	0,9827	0,9832
2,40	0,9836	0,9840	0,9845	0,9849	0,9853	0,9857	0,9861	0,9865	0,9869	0,9872
2,50	0,9876	0,9879	0,9883	0,9886	0,9889	0,9892	0,9895	0,9898	0,9901	0,9904
2,60	0,9907	0,9909	0,9912	0,9915	0,9917	0,9920	0,9922	0,9924	0,9926	0,9929
2,70	0,9931	0,9933	0,9935	0,9937	0,9939	0,9940	0,9942	0,9944	0,9946	0,9947
2,80	0,9949	0,9950	0,9952	0,9953	0,9955	0,9956	0,9958	0,9959	0,9960	0,9961
2,90	0,9963	0,9964	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972
3,00	0,9973	0,9974	0,9975	0,9976	0,9976	0,9977	0,9978	0,9979	0,9979	0,9980
3,10	0,9981	0,9981	0,9982	0,9983	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986
3,20	0,9986	0,9987	0,9987	0,9988	0,9988	0,9988	0,9989	0,9989	0,9990	0,9990
3,30	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
3,40	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995	0,9995
3,50	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997	0,9997

Приложение 2. Значения t-критерия Стьюдента

при уровне значимости a: 0,10, 0,05, 0,01

Число степеней свободы ν	a	Число степеней свободы ν	a
0,1	0,05	0,01	0,1	0,05	0,01
	6,314	12,706	63,66		1,734	2,101	2,878
	2,92	4,3027	9,925		1,729	2,093	2,861
	2,353	3,1825	5,841		1,725	2,086	2,845
	2,132	2,7764	4,604		1,721	2,08	2,831
	2,015	2,5706	4,032		1,717	2,074	2,819
	1,943	2,4469	3,707		1,714	2,069	2,807
	1,895	2,3646	3,5		1,711	2,064	2,797
	1,86	2,306	3,355		1,708	2,06	2,787
	1,833	2,2622	3,25		1,706	2,056	2,779
	1,813	2,2281	3,169		1,703	2,052	2,771
	1,796	2,201	3,106		1,701	2,048	2,763
	1,782	2,1788	3,055		1,699	2,045	2,756
	1,771	2,1604	3,012		1,697	2,042	2,75
	1,761	2,1448	2,977		1,684	2,021	2,705
	1,753	2,1315	2,947		1,671		2,66
	1,746	2,1199,	2,921		1,658	1,98	2,617
	1,74	2,1098	2,898		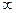1,645	1,96	2,576

Приложение 3. Значения F-критерия Фишера

при уровне значимости a = 0,05

ν1 ν2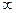
	161,5		215,7	224,6	230,2		238,9	243,9		254,3
	18,5		19,16	19,25	19,3	19,33	19,37	19,41	19,45	19,5
	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,15		3,84	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41	3,23
	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12	2,93
	5,12	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,9	2,71
	4,96	4,1	3,71	3,48	3,33	3,22	3,07	2,91	2,74	2,54
	4,84	3,98	3,59	3,36	3,2	3,09	2,95	2,79	2,61	2,4
	4,75	3,88	3,49	3,26	3,11		2,85	2,69	2,5	2,3
	4,67	3,8	3,41	3,18	3,02	2,92	2,77	2,6	2,42	2,21
	4,6	3,74	3,34	3,11	2,96	2,85	2,7	2,53	2,35	2,13
	4,54	3,68	3,29	3,06	2,9	2,79	2,64	2,48	2,29	2,07
	4,49	3,63	3,24	3,01	2,85	2,74	2,59	2,42	2,24	2,01
	4,45	3,59	3,2	2,96	2,81	2,7	2,55	2,38	2,19	1,96
	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,15	1,92
	4,38	3,52	3,13	2,9	2,74	2,63	2,48	2,31	2,11	1,88
	4,35	3,49	3,1	2,87	2,71	2,6	2,45	2,28	2,08	1,84
	4,32	3,47	3,07	2,84	2,68	2,57	2,42	2,25	2,05	1,81
	4,3	3,44	3,05	2,82	2,66	2,55	2,4	2,23	2,03	1,78
	4,28	3,42	3,03	2,8	2,64	2,53	2,38	2,2		1,76
	4,26	3,4	3,01	2,78	2,62	2,51	2,36	2,18	1,98	1,73
	4,24	3,38	2,99	2,76	2,6	2,49	2,34	2,16	1,96	1,71
	4,22	3,37	2,98	2,74	2,59	2,47	2,32	2,15	1,95	1,69
	4,21	3,35	2,96	2,73	2,57	2,46	2,3	2,13	1,93	1,67
	4,2	3,34	2,95	2,71	2,56	2,44	2,29	2,12	1,91	1,65
	4,18	3,33	2,93	2,7	2,54	2,43	2,28	2,1	1,9	1,64
	4,17	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,89	1,62
	4,12	3,26	2,87	2,64	2,48	2,37	2,22	2,04	1,83	1,57
	4,08	3,23	2,84	2,61	2,45	2,34	2,18		1,79	1,52
	4,06	3,21	2,81	2,58	2,42	2,31	2,15	1,97	1,76	1,48
	4,03	3,18	2,79	2,56	2,4	2,29	2,13	1,95	1,72	1,44
		3,15	2,76	2,52	2,37	2,25	2,1	1,92	1,7	1,39
	3,98	3,13	2,74	2,5	2,35	2,23	2,07	1,89	1,67	1,35
	3,96	3,11	2,72	2,49	2,33	2,21	2,06	1,88	1,65	1,31
	3,95	3,1	2,71	2,47	2,32	2,2	2,04	1,86	1,64	1,28
	3,94	3,09	2,7	2,46	2,3	2,19	2,03	1,85	1,63	1,26
	3,92	3,07	2,68	2,44	2,29	2,17	2,01	1,83	1,6	1,21
	3,9	3,06	2,66	2,43	2,27	2,16		1,82	1,59	1,18
	3,89	3,04	2,65	2,42	2,26	2,14	1,98	1,8	1,57	1,14
	3,87	3,03	2,64	2,41	2,25	2,13	1,97	1,79.	1,55	1,1
	3,86	3,02	2,63	2,4	2,24	2,12	1,96	1,78	1,54	1,07
	3,86	3,01	2,62	2,39	2,23	2,11	1,96	1,77	1,54	1,06
	3,85		2,61	2,38	2,22	2,1	1,95	1,76	1,53	1,03
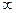
	3,84	2,99	2,6	2,37	2,21	2,09	1,94	1,75	1,52

[1] От лат. status – состояние, положение вещей; первоначально термин употреблялся в значении «политическое состояние»

[2] Эту деятельность на профессиональном уровне осуществляет государственная статистика – Федеральная служба государственной статистики (ФСГС) и система ее учреждений, организованных по административно-территориальному признаку, а также ведомственная статистика (на предприятиях, ведомствах, министерствах и т.д.). Информация ФСГС публикуется в специадльных печатных изданиях, а также в сети Интернет: www.gks.ru (или www.fsgs.ru)

[3] Термин «статистика» как параметр, как статистический критерий употребляется преимущественно в математической статистике, некоторые из них (χ², t и др.) рассмотрены в соответствующих темах данного курса лекций

[4] «There are three types of lies - lies, damn lies, and statistics» (Benjamin Disraeli, 1804 – 1881)

[5] «As a general rule, the most successful man in life is the man who has the best information»

[6] f – это начальная буква англ. слова frequency – частота

[7] В статистике, в отличие от математики, пределы суммирования не ставятся, а подразумеваются, так как абсолютные величины здесь не абстрактные, а смысловые (суммируются все величины совокупности – с первой по последнюю)

[8] Во многих учебниках по статистике встречается другое название индекса динамики – темп роста. Использование такого названия не совсем логично, так динамика может быть различна (не только рост, но и спад, а также стабильность), поэтому наиболее правильным является использование названия «индекс динамики» или «индекс изменения»

[9] Часто встречается и другое название темпа изменения – темп прироста, что не совсем логично (см. предыдущую сноску)

[10] Обычно (в т.ч. и в дальнейшем в данном пособии) в статистических формулах пределы суммирования не ставятся, а подразумеваются, т.е. подразумеваются именно такие пределы как формуле (11) – с 1-ой группы по N -ю (последнюю)

[11] Если приходится иметь дело с интервальным рядом распределения с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала, полученное значение называется плотностью ρ, то есть ρ = f/h

[12] Единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается

[13] От греч. «гистос» – ткань, строение

[14] От греч. слов «поли» и «гонос» – многоугольник

[15] При четном числе единиц совокупности за медиану принимают полусумму из двух центральных вариант

[16] Получите формулы и произведите их расчет (по аналогии с формулами для расчета квартилей) самостоятельно

[17] Максимально возможные значения показателей вариации: Л_max =;;;

[18] При расчете параметров уравнения тренда на ЭВМ необходимость вести отсчет от середины ряда динамики отпадает. Например, для получения уравнения тренда в Microsoft Office Excel необходимо построить его график с помощью «Мастера диаграмм», после чего вызвать контекстное меню, нажав на правую кнопку мыши на построенном графике, и выбрать пункт «Добавить линию тренда», в появившемся окне выбрать подходящую математическую функцию и установить галочку «показывать уравнение на диаграмме»

[19] Используется при малом количестве уровней (n <30), в противном случае (n >30) вместо используют коэффициент доверия t нормального закона распределения (Приложение 1)

[20] Проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо

[21] Термин «стохастический» происходит от греч. «stochos» – мишень. Стреляя в мишень, даже хороший стрелок редко попадает в ее центр, выстрелы ложатся в некоторой близости от него. Другими словами стохастическая связь означает приблизительный характер значений признака

[22] Термин «корреляция» ввел в статистику английский биолог и статистик Ф. Гальтон в конце XIX в., под которым понималась «как бы связь», т.е. связь в форме, отличающейся от функциональной. Еще ранее этот термин применил француз Ж.Кювье в палеонтологии, где под законом корреляции частей животных он понимал возможность восстановить по найденным в раскопках частям облик всего животного

[23] Множественная корреляция изучается в курсе эконометрики на основе применения компьютерных программ (напр., специальная надстройка к Excel, SPSS и др.), в курсе статистики изучается только парная корреляция

Дата добавления: 2014-01-03