Гистограмма. Гистограмма - это инструмент позволяющий зрительно оценить закон распределения величины разброса данных

Гистограмма - это инструмент позволяющий зрительно оценить закон распределения величины разброса данных, а также принять решение о том, на чем следует сфокусировать внимание для целей улучшения процесса.

Гистограмма отображается серией столбиков одинаковой ширины, но разной высоты. Ширина столбика представляет интервал в диапазоне наблюдений, высота — количество наблюдений (измерений), попавших в данный интервал. При нормальном законе распределения данных существует тенденция расположения большинства результатов наблюдений ближе к центру распределения (к центральному значению) с постепенным уменьшением при удалении от центра.

Гистограмма применяется главным образом для анализа значений измеренных параметров, но может использоваться и для оценки показателей возможностей процессов

Систематизируя показатели качества и анализируя построенную для них гистограмму, можно легко понять вид распределения, а определив среднее значение показателя и стандартное отклонение, можно провести сравнение показателей качества с контрольными нормативами и таким образом получить информацию высокой точности.

В связи с тем что теория управления качеством продукции во многих случаях базируется на использовании так называемого нормального закона распределения, рассмотрим этот закон подробнее.

Плотность р(х) нормального распределения случайной величины х выражается функцией

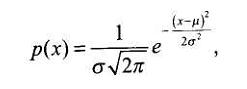
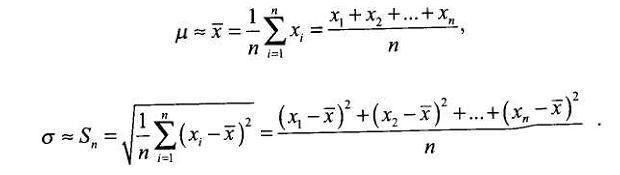
Приведем дополнительные сведения о вероятности попадания случайной величины х, распределенной по нормальному закону, в часто используемые интервалы.

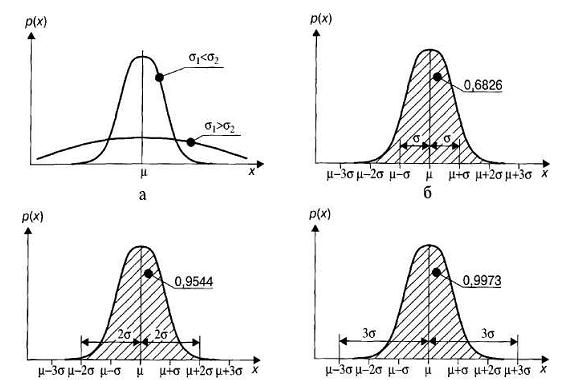
На рис. 3.1а приведены графики функции (3.1) при двух значениях параметра σ. Видно, что при значении σ1 < σ2 колоколообразная кривая падает по обе стороны от вершины более круто, чем при σ2 > σ1. С увеличением параметра σ кривая становится более покатой. Однако независимо от значения параметра σ площадь под кривой, представляющей собой функцию (3.1), равна единице.

Колоколообразная кривая имеет две точки перегиба, расстояние от которых до ординаты вершины, т. е. до вертикали, проведенной через математическое ожидание х = µ, равно среднеквадратичному отклонению σ. Заштрихованная на рис. 3.1б площадь криволинейной трапеции, заключенная между ординатами

х = µ - σ и х = µ + σ, равна 0,6826.

Это означает, что вероятность того, что случайная величина х, распределенная в соответствии с нормальным законом (3.1), находится в интервале

(µ - σ < х < µ + σ) и равна 0,6826, т. е.

Вер (µ - σ < х < µ + σ) = 0,6826.

Если рассмотреть (см. рис. 3.1в) интервал (µ - 2σ < х < µ + 2σ), то

Вер (µ - 2σ < х < µ + 2σ) = 0,9544.

Аналогично (см. рис. 3.1г) получается

Вер (µ - 3σ < х < µ + 3σ) = 0,9973.

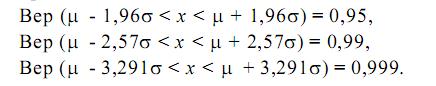
4.3.4. Диаграмма разброса

Диаграмма разброса позволяет без математической обработки экспериментальных данных о значениях двух переменных на основе графического представления этих данных оценить характер и тесноту связи между ними. Это дает возможность линейному персоналу контролировать ход процесса, а технологам и менеджерам — управлять им.

Этими двумя переменными могут быть:

4. характеристика качества процесса и фактор, влияющий на ход процесса;

5. две различные характеристики качества;

6. два фактора, влияющие на одну характеристику качества.

Рассмотрим примеры использования диаграмм разброса в указанных слу­чаях [15].

К примерам применения диаграммы разброса для анализа зависимости между причинным фактором и характеристикой (следствием) относятся диаграммы для анализа зависимости суммы, на которую заключены контракты, от числа поездок бизнесмена с целью заключения контрактов (планирование эффективных поез­док); процента брака от процента невыхода на работу операторов (контроль пер­сонала); числа поданных предложений от числа циклов (от времени) обучения персонала (планирование обучения); расхода сырья на единицу готовой продук­ции от степени чистоты сырья (стандарты на сырье); выхода реакции от темпера­туры реакции; толщины плакировки от плотности тока; степени деформации от скорости формовки (контроль процессов); размера принятого заказа от числа дней, за которое производится обработка рекламаций (инструкции по ведению торго­вых операций, инструкции по обработке рекламаций) и т. д.

При наличии корреляционной зависимости причинный фактор оказывает очень большое влияние на характеристику, поэтому, удерживая этот фактор под контролем, можно достичь стабильности характеристики. Можно также определить уровень контроля, необходимый для требуемого показателя каче­ства.

Примерами применения диаграммы разброса для анализа зависимости между двумя причинными факторами могут служить диаграммы для анализа зависимо­сти между содержанием рекламаций и руководством по эксплуатации изделия (движение за отсутствие рекламаций); между циклами закалки отожженной ста­ли и газовым составом атмосферы (контроль процесса); между числом курсов обучения оператора и степенью его мастерства (планирование обучения и подго­товки кадров) и т. д.

При наличии корреляционной зависимости между отдельными факторами зна­чительно облегчается контроль процесса с технологической, временной и эконо­мической точек зрения.

Применение диаграммы разброса для анализа зависимости между двумя характе­ристиками (результатами) можно видеть на таких примерах, как анализ зависимос­ти между объемом производства и себестоимостью изделия; между прочностью на растяжение стальной пластины и ее прочностью на изгиб; между размерами комп­лектующих деталей и размерами изделий, смонтированных из этих деталей; между прямыми и косвенными затратами, составляющими себестоимость изделия; между толщиной стального листа и устойчивостью к изгибам и т. д.

При наличии корреляционной зависимости можно осуществлять контроль только одной (любой) из двух характеристик.

Построение диаграммы разброса (поля корреляции) производят следующим образом.

Планируют и выполняют эксперимент, при котором реализуется взаимо­связь y = f(x), либо производят сбор данных о работе организации, об из­менениях в обществе и т. п., в которых выявляется взаимосвязь y = f(x). Первый путь получения данных характерен для технических (конструк­торских или технологических) задач, второй путь — для организационных и социальных задач. Желательно получить не менее 25-30 пар данных, ко­торые заносят в таблицу. Таблица имеет три графы: номер опыта (или де­тали), значения у и х.

Оценивают однородность экспериментальных данных с помощью критери­ев Груббса или Ирвина [18]. Резко выделяющиеся результаты, не принадле­жащие данной выборке, исключают попарно.

Находят максимальные и минимальные значения x и у. Выбирают масшта­бы по оси ординат (у) и оси абсцисс (x) так, чтобы изменение факторов по этим осям имело место на участках примерно одинаковой длины. Тогда диаграмму будет легче читать. На каждой оси нужно иметь 3-10 градаций. Желательно использовать целые числа.

Для каждой пары значений y. — x. на графике получают точку как пересече­ние соответствующих ординаты и абсциссы. Если в разных наблюдениях по­лучены одинаковые значения вокруг точки, рисуют столько концентричных кружков, сколько этих значений минус одно, либо наносят все точки рядом, либо рядом с точкой указывают общее число одинаковых значений.

На диаграмме или рядом с ней указывают время и условия ее построения (общее число наблюдений, Ф. И. О. оператора, собравшего данные, средства измерений, цена деления каждого из них и др.).

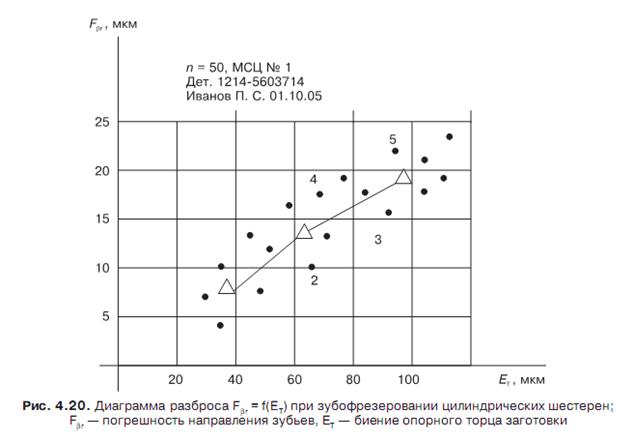
Для построения эмпирической линии регрессии диапазон изменения x (или у) разбирают на 3-5 равных частей. Внутри каждой зоны для попавших в нее точек находят X] и у ■ (j — номер зоны). Наносят эти точки на диаграмму (на рис. 4.20 они обозначены треугольниками) и соединяют между собой. По­лученная ломаная более наглядно иллюстрирует вид зависимости y = f (x).

Эмпирическую линию регрессии строят обычно на этапе обработки опытных данных, но даже само расположение точек диаграммы рассеяния в факторном пространстве (y — x) без построения этой линии позволяет предварительно оце­нить вид и тесноту взаимосвязи y = f(x).

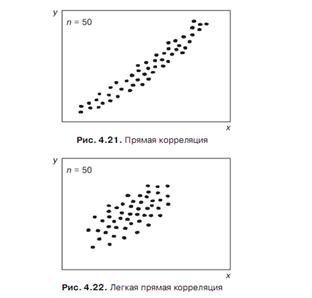
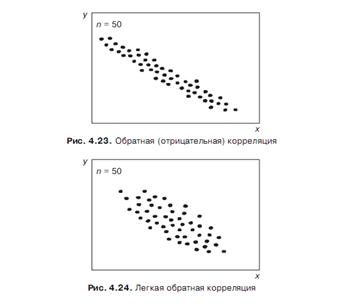
Взаимосвязь двух факторов может быть линейной (рис. 4.21-4.24) или нелиней­ной (рис. 4.26, 4.27), прямой (см. рис. 4.21, 4.22) или обратной (см. рис. 4.23, 4.24), тесной (см. рис. 4.21, 4.23, 4.27) или слабой (легкой) (см. рис. 4.22, 4.24, 4.26) или вообще отсутствовать (рис. 4.25).

Для линейной зависимости, как известно, характерно прямо пропорциональ­ное изменение у при изменении x, которое может быть описано уравнением пря­мой линии:

у = а + bx. (4.3)

Линейная зависимость является прямой, если имеет место увеличение значе­ний y при увеличении значений х. Если с ростом x значения y уменьшаются — зависимость между ними обратная.

Если имеет место закономерное изменение положения точек на диаграмме рас­сеяния, когда с изменением x происходит линейное или нелинейное изменение у, значит, существует взаимосвязь между у и x. Если такого изменения положения точек нет (см. рис. 4.25), значит, связь между у и x отсутствует. При наличии свя­зи малый разброс точек относительно их воображаемой средней линии свидетель­ствует о тесной связи у с x, большой разброс точек — о слабой (легкой) связи у с x.

После качественного анализа зависимости у = f(x) по форме и расположению диаграммы рассеяния выполняют количественный анализ этой зависимости. При этом часто используют такие методы, как метод медиан [15, 19], метод сравнения графиков изменения значений у и x во времени или контрольных карт для этих значений [15], оценка временного лага взаимосвязи переменных [4], методы кор­реляционно-регрессионного анализа [18, 19].

Первые два из перечисленных методов предназначены для оценки наличия и ха­рактера взаимосвязи (корреляции) между у и x. Достоинство этих методов — от­сутствие сложных расчетов. Рекомендуются при обработке результатов непосред­ственно на рабочем месте, где производились измерения. Методы реализуются путем подсчета точек в определенных зонах диаграммы рассеяния или контрольной карты, их суммирования и сравнения полученных значений с табличными. Мето­ды не дают количественной оценки степени тесноты связи у и x.

Третий метод используется для определения периодов времени, когда между двумя характеристиками качества существует наиболее тесная взаимосвязь. Для этого строятся и анализируются диаграммы разброса между значениями у1 — xt со сдвигом во времени. Сначала строятся диаграммы между значениями у1 — x, за­тем у1 +1 — x, затем у1 + 2 — xt и т. д. Здесь i — период времени, в который измеря­лись значения у и x. Это могут быть час, день, месяц и т. п.

Наиболее объективную, количественную оценку степени тесноты и характера взаимосвязи между значениями изучаемых параметров у и x можно получить при использовании методов корреляционно-регрессионного анализа (КРА). Досто­инством этих методов является также то, что достоверность их результатов под­дается оценке.

Степень тесноты линейной взаимосвязи между двумя факторами оценивается с помощью коэффициента парной корреляци:

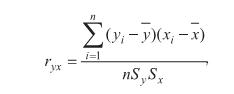
Дата добавления: 2014-01-03