Типы неопределенностей и методы их раскрытия

Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей.

I. Неопределенность вида .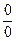

Пример. Вычислить предел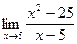

При подстановке вместо переменной х числа 5 видим, что получается неопределенность вида 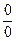. Для ее раскрытия нужно разложить числитель на множители: (х ² – 25 = (х– 5)∙(х+ 5)), получили общий множитель (х– 5), на который можно сократить дробь. Заданный предел примет вид: 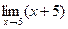. Подставив х= 5, получим результат.

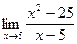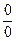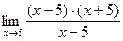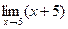= = = =5+5 =10

Пример. Вычислить предел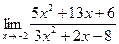

При подстановке вместо переменной х числа - 2 видим, что получается неопределенность вида 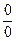. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х+ 2. В результате получим новый предел, знаменатель которого при подстановке вместо переменной х числа -2 не равен нулю. Этот предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.

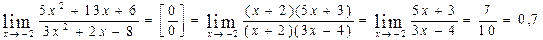
II. Неопределенность вида .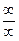

Для раскрытия этой неопределенности нужно каждое слагаемое числителя и знаменателя разделить на переменную в наибольшей степени и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность.

Пример. Вычислить предел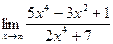

Здесь числитель и знаменатель не имеют предела, т.к. оба неограниченно возрастают. В этом случае имеем неопределенность вида 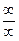. Для ее раскрытия разделим каждое слагаемое на переменную в наибольшей степени, т.е. на х ⁴. Получим:

= =

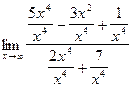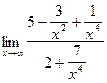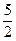
Величины 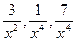являются бесконечно малыми при 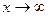и их пределы равны нулю. Следовательно, искомый предел равен .

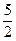Пример. Вычислить предел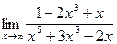

Имеем неопределенность вида 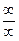. Аналогично предыдущему примеру разделим числитель и знаменатель на х ⁵. Получим:

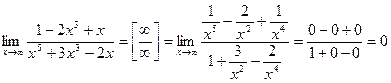
Пример. Вычислить предел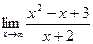

Имеем неопределенность вида 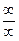. Разделим числитель и знаменатель на х ². Получим:

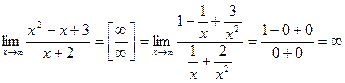
Дата добавления: 2014-01-03