Непрерывность некоторых элементарных функций

Свойства непрерывных функций

1) Сумма, разность и произведение непрерывных в точке х ₀ функций – есть функция, непрерывная в точке х ₀.

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х ₀.

3) Если у = f(u), где u = g(x) – непрерывные функции в точке х = х ₀, то функция y = f(g(x)) – также непрерывна в этой точке.

1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.

2) Рациональная функция 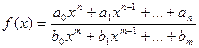непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

3) Тригонометрические функции непрерывны на своей области определения.

Вообще следует заметить, что все основные элементарные функции непрерывны на всей своей области определения.

Точки разрыва и их классификация

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х ₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х=х ₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если правый односторонний предел 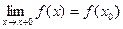, то функция называется непрерывной справа.

х ₀

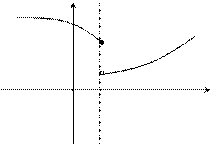
Если левый односторонний предел 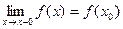, то функция называется непрерывной слева.

х ₀

Точка х ₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х ₀ или не является непрерывной в этой точке.

Классификация точек разрыва

1. Устранимый разрыв. Точка х ₀ называется точкой устранимого разрыва функции, если в этой точке функция f(x) не определена, но имеет конечный предел.

2. Разрыв 1-го рода. Точка х ₀ называется точкой разрыва 1-го рода функции, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.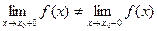

3. Разрыв 2-го рода. Точка х ₀ называется точкой разрыва 2-го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция f(x) = 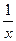имеет в точке х ₀ = 0 разрыв 2–го рода, т.к.

.

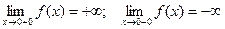Пример. f(x) =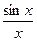

Функция не определена в точке х = 0, но имеет в ней конечный предел 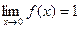, т.е. в точке х =0 функция имеет точку устранимого разрыва. Этот разрыв можно устранить, если доопределить функцию:

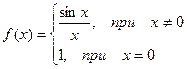
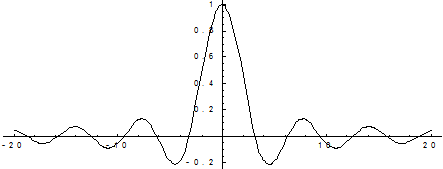
График этой функции:

Пример. f(x) = =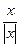

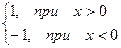
y

0 x

-1

Эта функция также обозначается sign(x). В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1–го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях будет иметь в точке х = 0 разрыв 1–го рода.

Дата добавления: 2014-01-03