Производственная функция

Производственными функциями называют соотношения между используемыми в производстве материальными благами и трудовыми ресурсами (называемыми в совокупности – производственными ресурсами), а также выпускаемой продукцией [2]. Тогда производственная функция связывает значение вектора продукции[1] у со значениями вектора ресурсов х:

F(x,y,a)=0 (2)

(где: х- количество ресурса, у – объем выпуска продукции, а – параметры функции. [2]

Соотношение (2) может быть векторным, т.е. оно может состоять из нескольких равенств и может быть задано не только в аналитическом виде, но и виде таблицы. Описание связи между использованием ресурсов и выпуском продукции в соотношении (1) подразумевает, что не учитываются эффекты, связанные с продолжительностью производственного цикла, т.е. с периодом между затратами ресурсов и выпуском продукции.

Два частных случая производственных функций:

1. Функция выпуска, в которой в качестве независимых переменных берутся затраты ресурсов, а функцией является выпуск: y=f(x,a), а – параметр производственной функции, х – количество ресурса.

2 Функция производственных затрат, в которой независимой переменной является выпуск, а функцией – затраты: х=f(y,a).

Как правило, под производственной функцией подразумевают функцию выпуска.

Производственная функция – функциональная взаимосвязь (зависимость) между вводимой комбинацией факторов производства и объемом выпуска продукции [1].

Q = F (x_a, x_b, x_c, … x_n), (1)

где: Q – объем выпуска (максимальное значение),

F – форма функциональной зависимости,

X_а …- факторы производства, ресурсы (м.б. альтернативно заменяемые факторы)

Если Х2>Х1, то F(X2)>F(X1): увеличение фактора увеличит выпуск.

……

В исследованиях используют понятия:

Краткосрочный период – хотя бы один фактор остается неизменным

Долгосрочный период – могут быть изменены все факторы производства,

Переменные факторы – ресурсы, количество которых может быть изменено в краткосрочном периоде.

Постоянные факторы – ресурсы, количество которых не может быть заменено при краткосрочном периоде.

Обычно делают предположение о непрерывном изменении переменных х и достаточно плавном изменении выпуска при изменении затрат ресурсов.

Показатели предельного анализа для функций выпуска, в т.ч. допускающих замену одного ресурса другим.

1. ТР_х – совокупный продукт от переменного фактора Х – это общий объем выпуска при данном количестве Х.

2. МР_х – предельный физический продукт – прирост общего продукта за счет единичного увеличения Х, МР_х = D ТР_х / DХ = dТР_х / dХ (первая производная от производственной функции). Частная производная производственной функции по одному из ресурсов является предельной производительностью (эффективностью) данного ресурса, МР_х = df / dХ_i. Она характеризует скорость изменения функции выпуска по отношению к изменению затрат ресурсов.

3. Средней производительностью ресурса будет показатель АР_х = f(x)/x_i. АР_х – средний продукт – объем выпуска на единицу Х, АР_х = ТР_х /Х

4. Относительной характеристикой изменения выпуска продукции при увеличении затрат ресурсов будет показатель эластичности выпуска по отношению к изменению затрат i-го ресурса: . Эластичность выпуска по отношению к изменению затрат ресурса показывает, на сколько процентов возрастет объем продукции при увеличении затрат ресурсов на 1%.

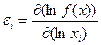(другая формула)

Дата добавления: 2014-01-03