КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические операции
|
|
|
|
Отрицанием высказывания Р является новое высказывание, которое является истинным, если высказывание Р ложно и наоборот. Обозначается 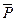 . Читается «не Р», «неверно, что Р». Все логические значения высказывания описаны с помощью таблицы 1. Можно образовать
. Читается «не Р», «неверно, что Р». Все логические значения высказывания описаны с помощью таблицы 1. Можно образовать 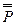 - двойное отрицание высказывания Р. Логические значения
- двойное отрицание высказывания Р. Логические значения 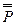 совпадают со значениями Р.
совпадают со значениями Р.
Таблица 1
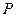
| 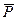
| 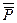
|
Конъюнкция (логическое умножение двух высказываний) – это новое высказывание R, которое истинно только тогда, когда оба высказывания истинны, и ложно, когда хотя бы одно из них ложно. Обозначается P & Q, 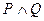 , P · Q или PQ. Читается: «P и (а, но, однако, хотя и т.д.) Q». Таблица истинности конъюнкции дана в таблице 2.
, P · Q или PQ. Читается: «P и (а, но, однако, хотя и т.д.) Q». Таблица истинности конъюнкции дана в таблице 2.
Таблица 2
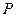
| 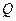
| 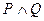
|
Союз «и» в алгебре логики используется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Например, «Луна сделана из зеленого сыра, и дронт вымер».
Дизъюнкцией (логическим сложением) двух высказываний P и Q называется новое высказывание, которое истинно, если хотя бы одно из высказываний истинно, и ложно, если оба ложны. Обозначается 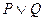 . Читается «P или Q». Логические значения дизъюнкции приведены в таблице 3.
. Читается «P или Q». Логические значения дизъюнкции приведены в таблице 3.
Таблица 3
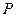
| 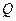
| 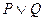
|
В повседневной речи союз «или» употребляется в различном смысле: исключающем или неисключающем. В алгебре логики связка 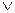 употребляется в неисключающем смысле. Например, «Виктор купил автомобиль, или у Ивана светлые волосы».
употребляется в неисключающем смысле. Например, «Виктор купил автомобиль, или у Ивана светлые волосы».
В исключающем смысле употребляется итерация, которая называется «строгая дизъюнкция (разделительное или)». Обозначается 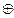 . Например, «Анна полетит в Москву самолетом, или она поедет на поезде (Нельзя одновременно лететь на самолете, или ехать на поезде)», «Сегодня понедельник или вторник». Таблица истинности для строгой дизъюнкции совпадает с таблицей истинности логической операции «сложение по модулю два» в булевой алгебре. Таблица истинности операции приведена в таблице 4.
. Например, «Анна полетит в Москву самолетом, или она поедет на поезде (Нельзя одновременно лететь на самолете, или ехать на поезде)», «Сегодня понедельник или вторник». Таблица истинности для строгой дизъюнкции совпадает с таблицей истинности логической операции «сложение по модулю два» в булевой алгебре. Таблица истинности операции приведена в таблице 4.
Таблица 4
| P | Q | 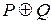
|
Как видно из таблицы 4, сложное высказывание при использовании строгой дизъюнкции истинно только тогда, когда истинно лишь одно из высказываний.
Импликацией (логическим следованием) двух высказываний P и Q называется новое высказывание, которое ложно, когда P истинно, а Q ложно, и истинно во всех остальных случаях. Обозначается 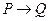 . Читается «если P, то Q» или «из P следует Q». Высказывание P является условием, посылкой, а высказывание Q – следствием, заключением. Например, если 2<5, то 7-8=11. Таблица истинности операции – это таблица 5.
. Читается «если P, то Q» или «из P следует Q». Высказывание P является условием, посылкой, а высказывание Q – следствием, заключением. Например, если 2<5, то 7-8=11. Таблица истинности операции – это таблица 5.
Таблица 5
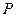
| 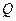
| 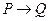
|
Употребление союзов «если... то» в алгебре логики отличается от употребления их в обыденной речи, где, как правило, считается, что если P ложно, то Q вообще не имеет смысла. Кроме того, в обыденной речи подразумевается, что из предложения P всегда вытекает Q. В математической логике этого не требуется, т.к. смысл высказываний игнорируется, учитывается только семантическая характеристика.
Эквиваленцией (логической эквивалентностью, эквивалентностью) двух высказываний P и Q называется новое высказывание, которое истинно, когда оба высказывания P и Q либо истинны, либо ложны одновременно, и ложно в остальных случаях. Обозначается 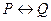 . Читается «для того, чтобы P,... необходимо и достаточно, чтобы Q», или «P – тогда и только тогда, когда Q». Эквивалентность играет большую роль в математических доказательствах: большое количество теорем формируется в форме необходимых и достаточных условий. Логические значения операции эквиваленция приведены в таблице 6.
. Читается «для того, чтобы P,... необходимо и достаточно, чтобы Q», или «P – тогда и только тогда, когда Q». Эквивалентность играет большую роль в математических доказательствах: большое количество теорем формируется в форме необходимых и достаточных условий. Логические значения операции эквиваленция приведены в таблице 6.
Таблица 6
| P | Q | 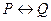
|
Символы ¬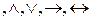 называются пропозициональными связками или связками исчисления высказываний. Вместо знака ↔ часто пишут ~ или
называются пропозициональными связками или связками исчисления высказываний. Вместо знака ↔ часто пишут ~ или 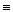 , вместо → употребляют
, вместо → употребляют 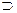 , вместо & или
, вместо & или 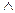 часто ставят точку, причем точку иногда опускают, вместо «−» употребляют знак
часто ставят точку, причем точку иногда опускают, вместо «−» употребляют знак 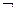 или ┐ перед высказыванием.
или ┐ перед высказыванием.
Не следует думать, что набором отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция исчерпываются все логические связки. Вышеперечисленные операции используются в логике высказываний. В булевой алгебре будут изучены операции штрих Шеффера │, стрелка Пирса ↓. Свои названия эти связки получили в честь математиков Г. Шеффера и Ч. Пирса. Этим связкам соответствуют
таблицы истинности 7 и 8.
| Таблица 7 | Таблица 8 | ||||||||||||||||||||||||||||||
|
|
Из анализа таблиц истинности можно сделать вывод, что операция Штрих Шеффера – это антиконъюнкция, а Стрелка Пирса – это антидизъюнкция.
Таблицы истинности
Каждая формула алгебры высказываний обладает свойством превращаться в высказывание при фиксации в ней значений всех высказывательных переменных, т.е. если мы зафиксируем в формуле значения всех высказывательных переменных, то, пользуясь определениями логических операций, мы можем вычислить значение истинности формулы.
Таблица истинности формулы алгебры высказываний содержит столько строк, сколько всевозможных наборов значений истинности переменных можно образовать. Так как каждая высказывательная переменная может принимать только два значения (0 и 1), то в случае n переменных таблица истинности содержит 2n строк.
При построении таблицы истинности наборы значений переменных располагают сверху вниз в лексикографическом порядке (каждый набор понимают как двоичную запись неотрицательного целого числа и располагают в порядке возрастания от (000…0) до (111…1)).
Если возникают трудности с использованием двоичной системы счисления, можно применить метод «последовательного половинного деления столбцов» - столбец первой переменной делят пополам и заполняют верхнюю половину нулями, а нижнюю половину – единицами, затем каждую половину второго столбца делят пополам и опять заполняют полученные половины нулями и единицами, и т.д. Последовательность такого заполнения приведена на рис. 1.
Затем в соответствии с порядком действий последовательно заполняют столбцы значений подформул, из которых образуется формула. Последним заполняется столбец значений истинности формулы.
| x1 | x2 | x3 |
| x1 | x2 | x3 |
| x1 | x2 | x3 |
рис.1
Пример 1. Построить таблицу истинности формулы: 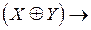
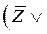
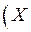 ï
ï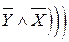 .
.
Решение. Порядок действий при построении таблицы исттинности совпадает с порядком столбцов таблицы 9.
Таблица 9.
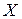
| 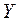
| 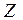
| 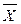
| 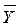
| 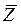
| 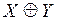
| 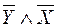
| 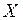 ï ï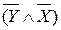
| 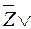 ( (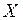 ï ï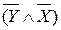 ) )
| 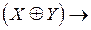 (
(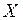 ï ï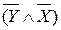 ) )
|
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 672; Нарушение авторских прав?; Мы поможем в написании вашей работы!