
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формулы алгебры логики
|
|
|
|
Тема 1.2 Законы алгебры логики
Формулы алгебры логики обозначаются большими буквами латинского алфавита A, B, C, D, …. Буквы, обозначающие высказывания, логические связки и скобки, составляют алфавит языков логических высказываний.
Алфавитом называется любое непустое множество. Элементы этого множества называются символами алфавита. Словом в данном алфавите называется произвольная конечная последовательность символов (возможно, пустая).
С помощью элементов алфавита можно построить различные логические формулы. Будем называть выражение, составленное из обозначений высказываний, логических связок и скобки, логической формулой, если оно удовлетворяет следующим условиям:
- любая переменная, обозначающая высказывание, - формула;
- если А и В формулы, то 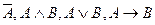 ,А~В – формулы;
,А~В – формулы;
- других формул нет.
Подформулой формулы А называется любое подслово А, само являющееся формулой.
Из вышеперечисленного можно сделать вывод и определить более простое понятие формулы.
Всякое сложное высказывание, которое может быть получено из элементарных высказываний с помощью логических связок, называется формулой алгебры логики.
Формула А называется тождественно-истинной (тавтологией), если на любых оценках списка переменных < X i1 , X i2, …, X ik > она принимает значение И (1).
Формула А называется выполнимой, если на некоторой оценке списка переменных < X i1 , X i2, …, X ik > она принимает значение И.
Формула А называется тождественно-ложной, если на любых оценках списка переменных < X i1 , X i2, …, X ik > она принимает значение Л (0).
Каждая формула алгебры логики принимает свое логическое значение, которое определяется логическими значениями входящих в нее элементарных высказываний. Истинностное значение функции может быть определено с помощью таблицы истинности.
Пример 2. Составить таблицу истинности для формулы 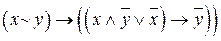 .
.
Таблица 10
| х | у | 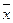
| 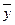
| 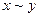
| 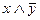
| 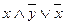
| 
| Итог |
Если формула состоит из n элементов, то ее таблица истинности состоит из 2n строк.
Какой бы сложной ни была формула, содержащая n переменных, для нее всегда найдется единственная соответствующая ей функция. Для одной и той же функции можно поставить в соответствие несколько различных формул.
Две различные формулы называются эквивалентными, если соответствующие им функции равны. Из единственности построения таблиц истинности для функций следует, что формулы эквивалентны, если их таблицы истинности совпадают.
Функция может быть представлена как операция, если все ее значения лежат в области определения этой же функции. В этом смысле все функции математической логики могут быть представлены операциями.
Подобные преобразования формул называются эквивалентными или тождественными.
Пример 3. 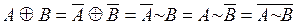
В справедливости этого утверждения предлагается убедиться самостоятельно, построив таблицы истинности.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 837; Нарушение авторских прав?; Мы поможем в написании вашей работы!