Высказываниями

Соотношение между множествами и составными

Существует тесная связь между множествами – с одной стороны, и высказываниями – с другой, а также между операциями над множествами, с одной стороны, и операциями образования составных высказываний – с другой.

Если рассматривается несколько высказываний, то сопоставить каждому из этих высказываний некоторое множество можно вполне логичным путем. Сначала мы образуем множество всех логических возможностей для рассматриваемых высказываний и назовем его универсальным множеством. Затем каждому высказыванию мы поставим в соответствие подмножество тех логических возможностей универсального множества, для которых это высказывание истинно.

Определение. Пусть X, Y, Z,... означают некоторые высказывания, и пусть U — их множество логических возможностей. Пусть А, В, С,... означа­ют подмножества U, для которых истинны соответственно высказывания X, Y, Z,.... Тогда А, В, С,... называются соответственно множествами ис­тинности высказываний X,Y,Z,....

Если X и Y — высказывания, то 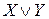и также высказывания и, следовательно, они должны иметь множества истинности.

Чтобы найти множество истинности высказывания 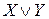, заметим что это высказывание истинно, когда истинно X или истинно Y (или оба). Таким образом, высказыванию 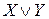мы должны поставить в соответствие те логические возможности, которые лежат в А или в В (или в них обоих); иначе говоря, мы должны поставить в соответствие 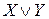множество . С другой стороны, высказывание истинно, только когда истинно и X и Y, так что высказыванию мы должны поставить в соответствие множество .

Итак, существует тесная связь между логической операцией дизъюнкцией и операцией объединения множеств, а также между конъюнкций и пересечением, а также между логической операцией отрицания и операцией дополнения множества, т.е. множеством истинности для 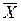будет .

Множество истинности двух высказываний X и Y показаны на диаграмме Эйлера-Венна (рис. 4). Здесь отмечены различные логические возможности этих высказываний.

рис. 4

Связь между высказыванием и его множеством истинности создает возможность «перевода» любой задачи, относящейся к составным высказываниям, в задачу теории множеств.

Возможно также и обратное: если поставлена какая-то задача, касающаяся множеств, то универсальное множество можно себе представить как некоторое множество логических возможностей, подмножества которого являются множествами истинности некоторых высказываний.

Следовательно, задачу, относящуюся к множествам, можно также «перевести» на язык составных высказываний.

Дата добавления: 2014-01-03