Соотношение между высказываниями и соответствующими им множествами истинности

Мы рассмотрели такие множества истинности составных высказываний, которые образованы посредством связок V, Λ, ^Ø. Все остальные связки можно определить через эти три основные и тем самым вывести, какие множества истинности им соответствуют. Например, известно, что импликация Х ® Y эквивалента дизъюнкции 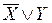. Поэтому множество истинности для Х ® Y будет тем же, что и множество истинности для 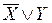, т. е. оно будет иметь вид .

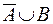На диаграмме Эйлера-Венна выделенная область показывает множество истинности этого высказывания (рис.5).

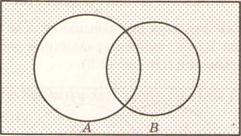
Рис. 5

Отметим, что незаштрихованная область на этой диаграмме показывает множество 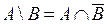, представляющее собой множество истинности высказывания 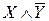. Поэтому заштрихованная область будет множеством 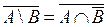, которое является множеством истинности высказывания 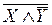. Таким образом, мы установили, что высказывания 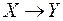, , 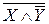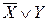эквивалентны. Вообще, два высказывания эквивалентны тогда и только тогда, когда они имеют одни и те же множества истинности.

Заметим, что диаграммы Эйлер – Венна помогают обнаруживать отношения между высказываниями.

Предположим теперь, что X – логически истинное высказывание. Что представляет собой его множество истинности? Поскольку высказывание X логически истинно тогда и только тогда, когда оно истинно в каждом логически возможном случае, множеством истинности для высказывания X должно быть универсальное множество U.

Подобным же образом, если высказывание X логически ложно, то оно ложно в каждом логически возможном случае, и поэтому его множеством истинности будет пустое множество .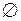

Рассмотрим отношение следствия. Напомним, что из X следует Y тогда и только тогда, когда импликация 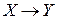логически истинна. Но высказывание 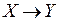тогда и только тогда логически истинно, когда его множество истинности совпадает с U, т.е. 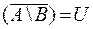и 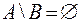. Но если 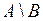пусто, то В включает в себя A. Отношение включения обозначается, как мы отмечали, 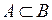и читается «A является подмножеством В». Таким образом, высказывание 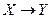логически истинно тогда и только тогда, когда .

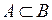Каждому высказыванию соответствует его множество истинности, каждой логической связке соответствует операции над множеством. Каждому отношению между высказываниями соответствует отношение между множествами истинности. Множествами истинности высказывани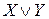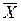й

; ;и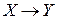

служат соответственно:

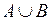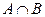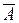; ; и .

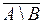Высказывание X логически истинно, если 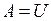, и логически ложно, если 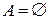. Высказывание X и Y эквивалентны тогда и только тогда, когда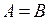; из Х следует Y тогда и только тогда, когда .

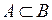Дата добавления: 2014-01-03