Показатель дисперсии, свойства и способы расчета

Дисперсия признака – s ² – определяется на основе средней квадратической степенной:

.

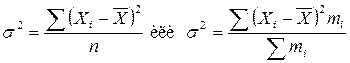Показатель s, равный 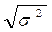, называется средним квадратическим отклонением. В теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов. Простыми преобразованиями могут быть получены формулы расчета дисперсии методом моментов:

.

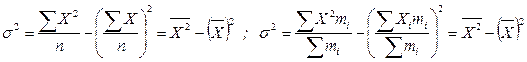Здесь 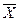– среднее значение признака (начальный момент первого порядка); 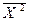– средняя величина квадратов значений признака (начальный момент второго порядка). Дисперсию признакаеще называют центральным моментом второго порядка. Формула метода моментов используется достаточно часто. На ней основываются, например, методы статистического имитационного моделирования.

Рассмотрим некоторые свойства показателя дисперсии.

Величина дисперсии не зависит от начала отсчета, т.е. все индивидуальные значения признака можно увеличить или уменьшить на одно и то же число. Это свойство очевидно, ибо с увеличением или уменьшением значений признака Х аналогично изменяется и показатель среднего уровня.

Численное значение дисперсии зависит от масштаба измерения X. При увеличении (или уменьшении) всех значений признака в С раз показатель дисперсии нового, увеличенного (или уменьшенного) признака будет больше (или меньше) дисперсии прежних значений в С² раз, т.е.

s²(Х×C) = C² · s²(X).

Эти свойства ускоряют расчеты, особенно если первичные данные представлены в сгруппированном виде с равными интервалами. Вводя вместо прежних значений признака Х новые, полученные по формуле

X^′_í = (X_i–A) / h,

убеждаемся, что

.

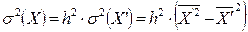Для приведенного ранее примера получаем

Xj^′	–2	–1
mj	0,09	0,18	0,24	0,49
(X^′j)^2·mj	0,36	0,18		0,49

Таким образом, .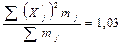

Так как 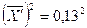, то s2 = 52·(1,03–0,0169) = 25,3275.

Непосредственный расчет по исходным данным оказывается более трудоемким.

Если вариация оценивается по небольшому числу наблюдений, взятых из достаточно большой генеральной совокупности, то математическое ожидание расчетной величины дисперсии оказывается смещенным в сторону уменьшения. Для получения несмещенной оценки рекомендуется дисперсию, полученную по приведенным ранее формулам, умножить на величину n/(n– 1 ). В итоге, при малом числе наблюдений (n <30) дисперсию признака рекомендуется вычислять по формуле

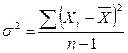или .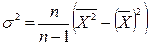

Обычно уже при n >(15÷20) расхождение смещенной и несмещенной оценки становится несущественным. По этой же причине обычно не вводят поправку и в формулу сложения дисперсий.

Если из генеральной совокупности сделать несколько выборок и каждый раз при этом определять среднее значение признака, то возникает задача оценки вариации средних. Оценить дисперсию среднего значения можно и на основе всего одного выборочного наблюдения по формуле

,

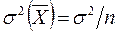где n – объем выборки; s² – дисперсия признака, рассчитанная по данным выборки. Величина 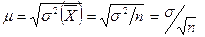носит название средней ошибки выборки и является характеристикой отклонения выборочного среднего значения признака Х от его истинной средней величины (от его математического ожидания). Показатель средней ошибки используется при оценке достоверности результатов выборочного наблюдения.

Дата добавления: 2014-01-03