Понятие и система показателей вариации

ТЕМА 5. СТАТИСТИЧЕСКИЙ АНАЛИЗ ВАРИАЦИИ

5.1. Понятие и система показателей вариации

5.2. Показатель дисперсии, свойства и способы расчета

5.3. Правило сложения дисперсий

5.4. Оценка вариации альтернативных признаков

Условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются конкретными количественными или атрибутивными уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления.

Для измерения вариации количественных признаков применяют несколько способов. Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным (Х_max) и минимальным (X_min) наблюдаемыми значениями признака.

Н = Х_max - X_min.

В показателе размаха вариации учитываются лишь крайние значения признака. Более точными характеристиками являются показатели колеблемости признака относительно среднего уровня. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня.

.

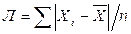При повторяемости отдельных значений Х применяют формулу средней арифметической взвешенной[6].

.

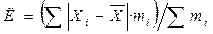Показатель линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но этот показатель плохо согласуется с вероятностными расчетами и усложняет применение методов математической статистики. Поэтому в статистических исследованиях для измерения вариации чаще всего используют показатель дисперсии и среднего квадратического отклонения (см. п.5.2).

Для сопоставления вариаций по нескольким признакам в одной и той же совокупности объектов или вариации одного и того же показателя по разным совокупностям характеристики вариации приводятся к относительному виду. Достигается это сравнением размаха вариации (Н), среднего линейного (Л) или среднего квадратического отклонения (σ) со средним уровнем того же признака. Получаемые величины называются коэффициентами вариации. Значения коэффициентов вариации обычно указывают в процентах. В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.[7] Формулы коэффициентов имеют вид:

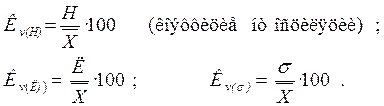
Дата добавления: 2014-01-03