Средние величины. Общие принципы их применения

Средняя величина (среднее значение, средний уровень или, для краткости, «средняя») – это обобщающий показатель, характеризующий типический уровень явления, образовавшийся в конкретных условиях места и времени. В средних величинах обобщается количественная вариация, погашаются индивидуальные различия единиц совокупности. Таким образом, среднее значение в отличие от конкретной величины признака позволяет сравнивать разные статистические совокупностям (например, средние уровни оплаты труда, средние уровни доходов населения и т.д.). Наблюдая изменение средней величины во времени, делают выводы об общей тенденции развития.

Принципы применения средних величин сводятся к следующему.

1. Необходим обоснованный выбор единицы совокупности, для которой рассчитывается среднее значение.

2. При расчете средней величины в конкретном случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь признаков и имеющиеся исходные данные.

3. Средние величины должны рассчитываться, прежде всего, по качественно однородным совокупностям. Однородные совокупности получают применяя метод группировок.

4. Общие средние для всей совокупности должны сопровождаться средними групповыми, например, показатель общей средней урожайности должен сопровождаться показателями урожайности в отдельных регионах, хозяйствах и т.д.

Средние величины делятся на два класса.

Степенные средние. Это наиболее известные и часто применяемые виды – средняя арифметическая величина, средняя гармоническая, средняя квадратическая и средняя геометрическая.

Структурные средние величины. В качестве структурных средних рассматривают моду и медиану.

Степенные средние величины рассматривают в формах простой и взвешенной средней. Средняя величина простая определяется по первичным не сгруппированным данным. Взвешенная средняя величина определяется по сгруппированным данным. Соответствующие формулы расчета имеют вид

,

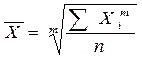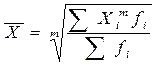
где X_i – варианта (значение) осредняемого признака; m – показатель степени средней; n – число вариант (наблюдений). f_i – частота, показывающая, сколько раз встречается i -e значение осредняемого признака.

В зависимости от значения показателя степени (m) получают:

· среднюю гармоническую величину, если m = –1;

· среднюю геометрическую величину, если m ® 0;

· среднюю арифметическую величину, если m = 1;

· среднюю квадратическую величину, если m = 2;

· среднюю кубическую величину, если m = 3 и т.д.

Соответствующие формулы расчета приведены в таблице 4.1. Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

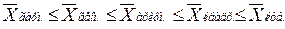
Таблица 4.1

Вид степенной средней	Показатель степени (m)	Формула расчета
Простая	Взвешенная
Гармоническая	–1		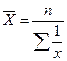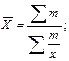m = xf
Геометрическая	→ 0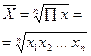
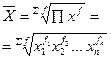
Арифметическая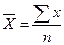
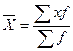
Квадратическая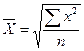

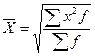
Пример.

Культура	Предприятие 1	Предприятие 2
Валовой сбор, ц	Урожайность, ц/га	Посевная площадь, га	Урожайность, ц/га
Пшеница
Рожь
Ячмень
Просо
Итого		-		-

Логическая формула показателя средней урожайности (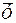) это отношение валового сбора (ВС) к посевной площади (ПП) –

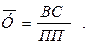
Для предприятия 1 известно значение числителя в логической формуле средней величины – показатели валового сбора. Величина знаменателя (ПП) определяется для каждой культуры как:

.

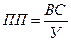В итоге получаем формулу расчета средней урожайности по сельскохозяйственному предприятию 1. Такую формулу имеет величина средняя гармоническая взвешенная; в качестве веса выступает валовой сбор. В знаменателе этого выражения определяется посевная площадь, под всеми культурами.

.

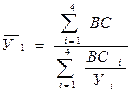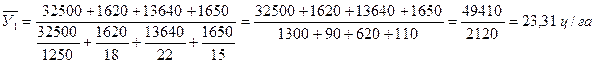
Для сельскохозяйственного предприятия 2 в условиях задачи присутствует численное значение знаменателя (показатель посевной площади – ПП). Числитель (ВС) по каждой культуре можно определить так:

ВС = У·ПП

Получаем формулу средней урожайности, где в качестве веса выступает посевная площадь. Такую формулу имеет средняя арифметическая взвешенная.

,

.

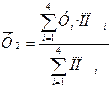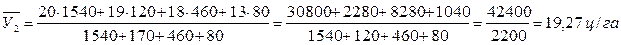В числителе определяется величина валового сбора зерновых.

Таким образом, расчет средней величины необходимо начинать с построения логической формулы, исходя из качественного содержания осредняемого показателя. Например,

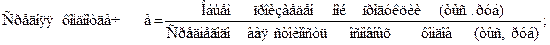
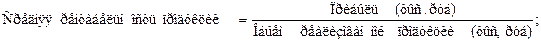
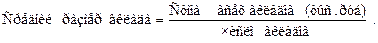
Для установления формулы средней величины А.Я. Боярский предложил использовать так называемый определяющий показатель. Средняя величина по этому методу должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или иным образом с осредняемым. Этот итоговый показатель и называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины.

Так, при расчете средней урожайности по предприятию 1 итоговым обобщающим показателем является общая посевная площадь (ПП), которая состоит из посевных площадей, занятых отдельными культурами:

.

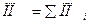В свою очередь, площадь, занятая отдельной культурой, связана с урожайностью соответствующей культуры соотношением

ПП_i = ВС_i / У_i.

Суммируя показатели посевной площади, получаем

.

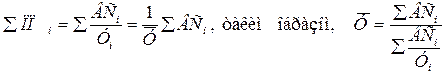Следовательно, при наличии данных о валовом сборе по видам культур и урожайности каждой культуры в отдельности среднее значение следует рассчитывать по формуле средней гармонической взвешенной:

Для предприятия 2 таким определяющим показателем является величина валового сбора (ВС). Величина валового сбора связана с урожайностью следующим образом:

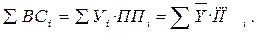Таким образом, .

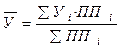При выборе определяющего показателя можно руководствоваться простым правилом: выделить три взаимно связанных показателя, включая и тот, по которому требуется рассчитать среднее значение. (В данном примере это валовой сбор (ц), посевная площадь (га), урожайность (ц/га)). Если имеются первичные данные по двум каким-либо показателям из этого списка, то отсутствующий третий показатель может служить определяющим признаком. (Для хозяйства № 1 отсутствовал показатель посевной площади, для хозяйства № 2 – показатель валового сбора). Если имеются данные по всем трем показателям, то исследователь вправе выбрать как среднюю величину арифметическую, так и среднюю гармоническую; при правильно назначенных весах результаты должны совпадать[5]. Если имеются данные только по тому признаку, для которого требуется рассчитать среднее значение, то исследователь вправе выбрать любую формулу степенной средней величины. В этих случаях рекомендуется также определять так называемые структурные средние (моду и медиану).

Правило определяющего показателя не следует абсолютизировать. Например, признаком цены товара обладает как та часть совокупности, которая порождает среднее значение - натуральная единица продукции, так и любая другая единица, интересующая исследователя. Например, различаются цены данного товара на отдельных торговых предприятиях, при различных ценах данного товара формируется каждый рубль издержек обращения, при различных ценах используется каждый квадратный метр торговой площади, при разных ценах реализуемого товара образуется тот или иной уровень рентабельности торговли и т.д. В этих случаях показателей, определяющих единый общий вид формулы среднего значения, фактически не существует, и исследователь вправе использовать подход, обычный в теории вероятностей и математической статистике - выбирать формулу простой арифметической средней или взвешивать индивидуальные уровни признака по их вероятностям.

Формула средней геометрической простой (не взвешенной) –

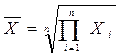
– используется обычно при расчете среднего значения по индивидуальным относительным величинам динамики. Такая средняя величина применяется, если задана последовательность цепных относительных величин динамики, указывающих на изменение показателя по сравнению с уровнем предыдущего периода: i₁, i₂, i₃,..., i_n. Например, объем производства в последнем году определяется его начальным уровнем (q₀) и последующим изменением по годам:

q_n = q₀ · i₁ · i₂ ·…· i_n.

Принимая q_n в качестве определяющего показателя и заменяя индивидуальные значения показателей динамики средними величинами, приходим к соотношению –

.

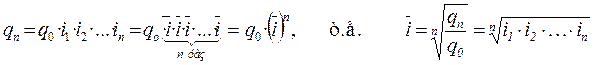Так, если ежегодно увеличить производства продукта на 7,2 % по отношению к предыдущему году, то в 10 году его производство возрастет в 2 раза.

К расчету показателя средних коэффициентов или темпов роста можно подойти и по иному. Примем в качестве определяющего показателя общий объем производства за n периодов (лет)

Q = q₁ + q₂+...+ q_n.

Тогда

Q = q₀ · i₁ + q₀ · i₁ · i₂ +... + q₀ · i₁ · i₂ ·... · i_n.

Заменяем индивидуальные значения коэффициентов средней величиной –

.

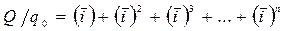Например, если задано, во сколько раз суммарный объем производства за n периодов (лет) должен превысить уровень базисного периода (года), то для определения среднего коэффициента роста надо решить уравнение степени n. Найденное среднее значение коэффициента роста дает ответ на вопрос, какими темпами должен ежегодно возрастать итоговый показатель, чтобы за ряд лет, начиная с базисного уровня q0, получился суммарный объем Q. Приведем таблицу решений при n = 3; 4; 5 для Q/q0 в интервале от 1 до 8:

n	Q / q0
	0,544	0,810		1,151	1,278	1,389	1,489	1,578
	0,519	0,741	0,888		1,091	1,169	1,237	1,298
	0,509	0,709	0,834	0,927		1,061	1,114	1,161
	0,504	0,692	0,805	0,885	0,948		1,044	1,083

Так, чтобы за предстоящие 5 лет произвести продукции в 6 раз больше, чем в предшествующем базисном году, следует ежегодно увеличивать объем производства на 6,1÷6,2 %.По сравнению с базисным годом производство должно составлять 106,1 %, 112,6 %, 119,6 %, 127,0 % и 134,7 %.

При анализе временных последовательностей (рядов динамики) единицей совокупности является момент или интервал времени. Это вносит разнообразие в расчет среднего значения. Появляются формулы хронологических средних величин для моментных и интервальных временных рядов, с равными и неравными интервалами. Средняя величина определяется с учетом основной закономерности изменения показателя во времени. Так, рассчитывая среднюю численность населения за ряд лет в условиях относительной устойчивости динамики, применяют формулу

,

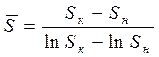где S_к, S_н – численность населения на конец и начало периода.

4.4. Расчет средней величины по результатам группировки.
Свойства средней арифметической

Если исходные данные представлены в сгруппированном виде, то средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических либо гармонических). Сложности возникают, когда в сгруппированных данных указываются не конкретные значения признака Х по каждой группе, а лишь интервалы его изменения. Правильный расчет общей средней величины возможен, если каким-либо образом удается установить средние значения признака в каждой группе. Если такие средние в группах определить по имеющимся сведениям нельзя, то их заменяют серединами интервалов, получая в итоге некоторое, чаще всего вполне удовлетворительное, приближение к среднему значению. Таким образом, расчет средней арифметической величины выполняют по формуле

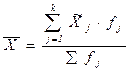, где .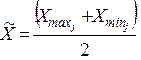

Расчет среднего значения по данным группировки требует, как всегда, обоснованного выбора взвешивающего показателя. Очень часто необходимые для анализа величины f_j – частоты повторения признака Х – в исходных данных либо отсутствуют, либо не столь очевидны.

Рассмотрим пример.

Группы предприятий	Себестоимость одного изделия, руб.	Число предприятий, %	Объем продукции, %	Затраты на производство, %
	110 – 115			8,2
	115 – 120			17,2
	120 – 125			23,9
	125 и выше			50,7
Итого	-

Если с определением середин интервалов никаких сложностей не возникает (112,5; 117,5; 122,5; 127,5), то при назначении взвешивающего показателя ошибкой может быть выбор признака “Число предприятий”, когда в процессе анализа рассматривается общая сумма затрат на производство. Умножение величины себестоимости одного изделия на число предприятий весьма косвенно характеризует общую сумму затрат на производство. Точную экономическую величину – оценку общих затрат на производство данной продукции получаем умножением себестоимости одного изделия на объем продукции. Таким образом, если использовать формулу средней арифметической, то в качестве взвешивающего показателя следует выбрать показатель объема продукции или его процентной доли в совокупном объеме производства. Тогда средняя себестоимость изделия будет равна

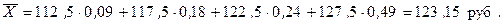
Такое же значение средней себестоимости в данном примере можно получить и по формуле средней гармонической, если в качестве взвешивающего признака использовать показатель “Затраты на производство”

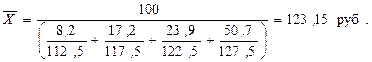
Заметим, что исходные данные задачи позволяют определить еще 2 показателя, косвенно характеризующие средний уровень себестоимости. А именно, 123,5 руб. – такая себестоимость единицы продукции приходится на 1% общего числа предприятий и 123,355 руб. – таков средний уровень себестоимости изделия, относящийся к 1 проценту общей суммы затрат.

Для ускорения ручных расчетов полезно знать следующие свойства:

1) величина средней арифметической не изменится, если веса всех вариантов заменить новыми, полученными из начальных умножением или делением на одно и то же число (s); действительно,

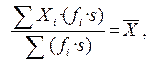
2) если все индивидуальные значения признака (т.е. все варианты) увеличить либо уменьшить в одно и то же число раз (или на одно и то же число), то среднее значение получившегося нового признака будет во столько же раз (или на столько же) отличаться от среднего значения исходного показателя. Действительно,

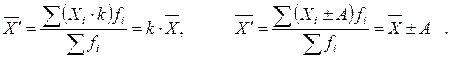
Свойство 1 используется для расчета средней величины через показатели удельного веса (частости). Свойство 2 применяют для ускорения ручных расчетов, особенно если первичные данные представлены в сгруппированном виде. Так, по приведенным данным найдем новую величину X΄, варианты которой определим по формуле –

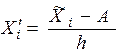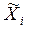, (– середина интервала i).

Тогда 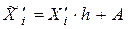. Переходим к средним величинам:

,

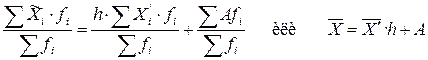Важно правильно выбрать величины А (обычно это середина какого-либо интервала) и h (чаще всего это величина интервала изменения признака в какой-либо группе).

Пусть, например, А = 122,5 и h = 5. Получаем последовательность величин X΄i: -2; -1; 0; 1. Их среднее значение равно 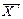= (-2)·0,09 + (-1)·0,18 + 0·0,24 + 1·0,49 = 0,13. Таким образом, 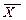= 5·0,13 + 122,5 =123,15 руб.

Дата добавления: 2014-01-03