Структурные средние величины

Структурные средни е применяются для изучения внутреннего строения совокупности значений признака и для оценки средней степенного типа, если по имеющимся статистическим данным её обоснованный расчет невозможен. Такая ситуация могла бы возникнуть, например, если в приведенной ранее таблице группировки предприятий по уровню себестоимости отсутствовали бы данные и об объеме производства, и о сумме затрат по группам предприятий.

В качестве структурных средних применяют показатель моды как наиболее часто повторяющегося значения признака и показатель медианы - величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части: в итоге у одной половины совокупности значение признака не превышает медианного уровня, а у другой - не меньше медианного.

Если изучаемый признак Х принимает только дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Так, для многоэтажного дома модальным значением признака «количество комнат в квартире» может оказаться число 3 (чаще всего квартиры 3-комнатные). Для определения медианного значения признака «количество комнат в квартире» следует выписать все квартиры в порядке возрастания числа комнат. Если получившийся ряд нечетный, то медианным значением будет количество комнат в квартире, находящейся в середине этого упорядоченного ряда. Если ряд четный, медианное значение оказывается числом, находящимся в определенном интервале (например, от 2 до 3 комнат).

Если данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), то расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, то оно оказывается в каком-то из интервалов признака X. Интерполяционным расчетом в этом, медианном интервале находят значение медианы Me по формуле:

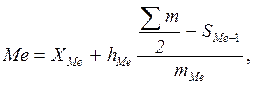
где Х_Me, h _{M e} — соответственно нижняя граница и величина медианного интервала; Σ т/2 - половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении); S_{Me- 1} - число наблюдений (или объем взвешивающего признака), накопленное до начала медианного интервала; m_Me - число наблюдений или объем взвешивающего признака в медианном интервале (в абсолютном или относительном выражении).

В нашем примере может быть получено даже три медианные значения себестоимости единицы продукции, исходя из признаков количества предприятий, объема продукции и общей суммы затрат на производство:

Ме ₁ = 125 + 5 (50-48)/52 = 125,19 руб.,

Ме ₂ = 120 + 5 (50-27)/24 = 124,79 руб.,

Me ₃ = 120 + 5 (50-49,3)/50,7 = 125,07 руб.

Таким образом, у половины предприятий уровень себестоимости единицы продукции превышает 125,19 руб., половина всего объема продукции производится с уровнем затрат на изделие, превышающем 124,79 руб., и 50% общей суммы затрат образовано при удельной себестоимости выше 125,07 руб. Заметим также, что отмечается некоторая тенденция к росту себестоимости, так как Ме ₂ - 124,79 руб., а средний уровень равен 123,15 руб.

Если признак Х принимает непрерывные значения (как это имеет место, например, с уровнем затрат на производство единицы продукции), то для расчета моды прежде всего необходимо представить первичные данные в форме интервального ряда распределения. Для определения моды интервального ряда выбирается модальный интервал. Если интервалы равные, то модальным называется тот интервал значений признака, в котором отмечается наибольшая абсолютная или относительная частота его (признака) повторяемости. Итак, для интервального ряда с равными интервалами величина моды определяется как

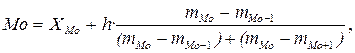
где Х_Mo - нижнее значение признака Х в модальном интервале; h - величина интервала; m_Mo - частота (частость) повторения признака Х в модальном интервале; m_{Mo -1}, m_{Mo +1} - соответственно, частоты (частости) признака для интервала, предшествующего модальному и следующего за ним;

Если первичные данные представлены неравными интервалами изменения признака Х, то модальным называется интервал, имеющий наибольшую плотность признака. Под плотностью в интервале понимается отношение частоты (абсолютной или относительной) признака Х к ширине соответствующего интервала. Тогда формула расчета моды получает вид:

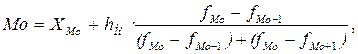
где Х_Mo - нижнее значение признака Х в модальном интервале (т.е. в интервале с максимальной плотностью); h_Мо - величина модального интервала; f_{Mo- 1}, f_Mo, f_{Mo+ 1} - соответственно, плотность признака для интервала, предшествующего модальному, плотность признака для модального интервала и плотность признака для интервала, следующего за модальным.

Для нашего примера можно рассчитать три модальных значения исходя из признаков числа предприятий, объема продукции и суммы затрат на производство. Во всех этих случаях модальный интервал один и тот же, так как для одного и того же интервала оказываются наибольшими и число предприятий, и объем продукции, и общая сумма затрат на производство:

Мо₁ = 125 + 5 (52-24)/((52-24)+(52-0)) = 126,75 руб.,

Мо₂ = 125+5 (49-24)/((49-24)+(49 - 0)) = 126,69 руб.,

Мо_з = 125 + 5 (50,7-23,9)/((50,7-23,911)) = 126,73 руб.

Таким образом, в нашем примере чаще всего встречаются предприятия с уровнем себестоимости 126,75 руб., чаще всего выпускается продукция с уровнем затрат 126,69 руб. и чаще всего затраты на производство определяются уровнем себестоимости 126,73 руб.

Контрольные вопросы

1. Понятие абсолютной величины в статистике, виды абсолютных величин, примеры абсолютных величин.

2. Понятие относительной величины в статистике, назначение и виды относительных величин, единицы измерения.

3. Относительные величины динамики, выполнения плана и планового задания и их взаимосвязь

4. Относительные величины структуры их взаимосвязь с показателями динамики.

5. Относительные величины координации и их взаимосвязь с показателями структуры.

6. Относительные величины сравнения и их взаимосвязь с показателями динамики.

7. Относительные величины интенсивности.

8. Понятие средней величины. Виды (формы) средних величин.

9. Правила выбора формулы средней величины.

10. Основные свойства средней арифметической величины. Расчета средней арифметической по данным ряда распределения.

11. Расчет медианного значения дискретных и непрерывных признаков.

12. Расчет модального значения дискретных и непрерывных признаков.

Дата добавления: 2014-01-03