
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ сезонных колебаний
Если в анализируемой временной последовательности наблюдаются устойчивые систематические отклонения от тенденции, то можно предположить наличие в этом ряду некоторых (одного или нескольких) колебательных процессов. Это особенно заметно, когда изучаемые явления имеют сезонный характер, – возрастание или убывание уровней повторяется регулярно с интервалом в один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т.д.).
Уровень сезонности оценивается с помощью индексов сезонности и гармонического анализа.
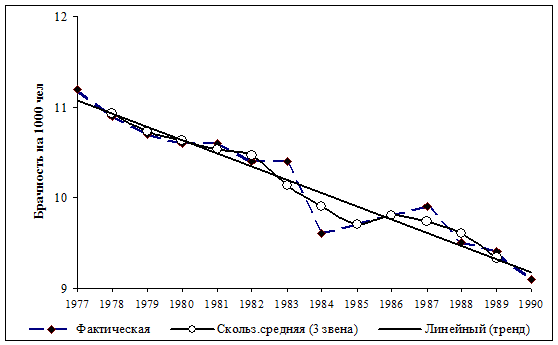
Рисунок 8.1. Графическое представление тенденции уровня брачности
Индексы сезонности показывают, во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня, вычисляемого по уравнению тенденции f(t). При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов нескольких лет. Индексы сезонности – это, по существу, относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции. Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.
Если тренда нет или он незначителен, то для каждого месяца (квартала)
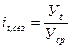 ,
,
где У t – уровень показателя за месяц (квартал) t; У ср – общий средний уровень показателя. Для обеспечения устойчивости показателей можно взять больший промежуток времени. В этом случае за Т лет рассчитывают:
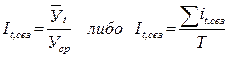
 ,
,
где 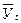 – средний уровень показателя по одноименным месяцам за ряд лет.
– средний уровень показателя по одноименным месяцам за ряд лет.
Пример. Имеются данные об объеме продаж акций на 15 крупнейших биржах России за 1993 г. (млн. руб.):
| Месяц | Уровень показателя (Yt) | it,сез |
| Январь | 12,78 | 0,027 |
| Февраль | 122,08 | 0,254 |
| Март | 709,98 | 1,477 |
| Апрель | 1602,61 | 3,334 |
| Май | 651,83 | 1,356 |
| Июнь | 220,80 | 0,459 |
| Июль | 327,68 | 0,682 |
| Август | 277,12 | 0,576 |
| Сентябрь | 418,31 | 0,870 |
| Октябрь | 521,18 | 1,084 |
| Ноябрь | 396,20 | 0,824 |
| Декабрь | 508,34 | 1,057 |
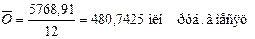
Как видно, в 1993 г. самый значительный пик объема продаж акций был зарегистрирован в марте–апреле–мае.
При наличии тренда индекс сезонности определяется на основе методов, исключающих влияние тенденции. Порядок расчета следующий:
1) для каждого уровня определяют выровненные значения по тренду f(t);
2) рассчитывают отношения it = Yt / f(t);
3) при необходимости находят среднее из этих отношений для одноименных месяцев (кварталов)
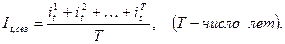
Другим методом изучения уровня сезонности является гармонический анализ. Его выполняют, представляя временной ряд как сумму гармонических колебательных процессов. Для каждой точки этого ряда справедливо выражение
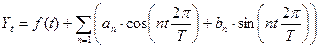 , t =1, 2,.... Т.
, t =1, 2,.... Т.
Здесь Yt – фактический уровень ряда в момент (интервал) времени t; f(t) – выровненный уровень ряда в тот же момент (интервал) t; an, bn – параметры колебательного процесса (гармоники) с номером n. Эти параметры в совокупности оценивают размах (амплитуду) отклонений от общей тенденции и сдвиг колебаний относительно начальной точки.
Общее число колебательных процессов, которые можно выделить для ряда, состоящего из Т уровней, равно Т /2. Обычно ограничиваются меньшим числом наиболее важных гармоник. Расчеты параметров гармоники достаточно трудоемки и выполняются в настоящее время на компьютерах по известным формулам математического анализа. Аппарат гармонического анализа позволяет оценить роль каждого колебательного процесса в общей вариации уровней временного ряда. Удельный вес гармоники с номером n определяется как dn = Дn / Д, где Д – дисперсия ряда, рассчитанная обычным способом; Дn –дисперсия, вносимая колебательным процессом (гармоникой) с номером n:
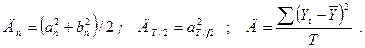
Для примера продаж акций обнаруживаем, что важнейшими колебательными процессами, проявившимися в данном временном ряду и объяснившими дисперсию ряда более, чем на 70 % были гармоника с номером 2 (два полных цикла на протяжении года) и гармоника с номером 3 (3 полных цикла в течение года). Уравнение, описывающее поведение ряда будет:
Yt = 480,74250 - 161,067·cos(2· t ·2 π /12) - 351,052·sin(2· t ·2 π /12)+
+254,002·cos(3· t ·2 π /12)-58.490·sin(3· t ·2 π /12).
|
Дата добавления: 2014-01-03; Просмотров: 894; Нарушение авторских прав?; Мы поможем в написании вашей работы!