Аналитический

Понятие функции. Способы задания

При изучении закономерностей, встречающихся в природе, приходится иметь дело с величинами постоянными и переменными.

О.3.1. Постоянной величиной называется величина, сохраняющая одно и то же значение (или вообще, или в данном процессе; в последнем случае постоянная величина называется параметром).

О.3.2. Переменной величиной называется величина, которая может принимать различные числовые значения.

Пример: диаметр и длина окружности в зависимости от постановки задачи могут принимать различные значения и, следовательно, эти величины являются переменными, однако отношение длины окружности к её диаметру сохраняет одно и то же значение 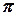= 3,14159….

Рассмотрим два множества действительных чисел 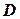и 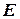и пусть задано соответствие: .

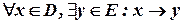Говорят, что задано отображение множества 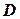на множество 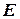. Записывают 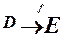, т.е. 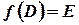или .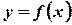

Отображение может быть неоднозначным: 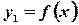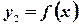. Наибольший интерес представляют отображения, при которых каждому элементу множества 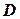соответствует только один элемент множества 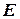. Такое отображение называется функцией.

Функцию 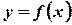можно рассматривать как отображение множеств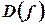а на 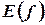. Вместо записи 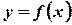пишут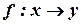

О.3.3. Отображение множества 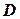на множество 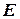называется функцией если для любого элемента множества 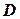существует элемент множества 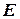и при том только один.

Кроме буквы 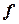для обозначения функций употребляются и другие буквы, например: 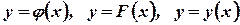. Аргумент так же может обозначаться не 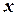, а другими буквами: 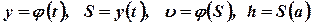и т.д.

Можно дать и другое определение функции.

0.3.4. Если для 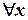из множества 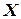по определенному закону ставится в соответствие переменная величина 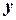из 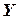, то говорят, что на множестве 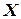определена функция 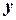переменной .

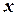Обозначение: 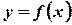; 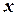- независимая переменная или аргумент, 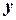- зависимая переменная или функция аргумента.

Множество 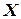- область определения функции 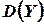, множество 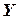-область значений.

О.3.5. Областью определения функции называется множество значений аргумента, при которых функция определена.

Способы задания функции

Задать функцию – это значит указать область ее определения и правило, при помощи которого по данному значению независимой переменной находится соответствующая ему значения функции.

Функции могут быть заданы самыми различными способами, но наиболее часто встречаются следующие: аналитический, табличный, графический, алгоритмический.

Функция определяется с помощью формулы, указывающей, какие действия надо совершить над значением аргумента, чтобы получить соответствующие значения функции.

При этом задании функции под областью ее определения (если нет дополнительных условий) понимают множество значений 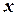, при которых формула, определяющая функцию имеет смысл.

Например:

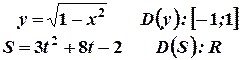
«+» 1) компактность задания

2) можно найти значения функции для 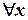из области определения

3) можно применить к функции аппарат математического анализа

«-» 1) недостаточная наглядность

2) необходимость вычислений иногда очень громоздких.

Одна функция на различных участках ее области определения задается различными формулами.

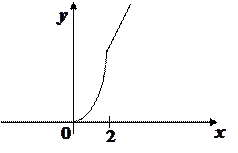Пример:

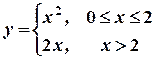
Дата добавления: 2014-01-03