Аналитическая геометрия в трехмерном пространстве

Напоминая снова о школьном курсе геометрии, перейдем от плоских представлений к пространственным. Аналогично тому, как мы переходили от координат на прямой к координатам на плоскости, проведем из начала координат О прямую, перпендикулярную плоскости ОXY. Что мы при этом получим? Систему декартовых координат в трехмерном пространстве.

Аналогично плоскости, определим вектор как упорядоченную пару точек в пространстве. Соответственно можно определить и координаты вектора,

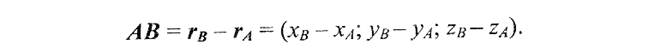Аналогично плоскости вычисляется и длина (модуль) вектора, только если на плоскости это была диагональ соответствующего прямоугольника, то теперь это будет диагональ прямоугольного параллелепипеда, построенного на разностях соответствующих координат.

Дальнейшие представления о скользящих и приложенных векторах строятся аналогично плоскому случаю, только, как уже подчеркивалось, каждый вектор характеризуется не двойкой, а тройкой чисел. Аналогично же вводится алгебра векторов: операции сложения и умножения на число. Нуль-вектор также присутствует в множестве трехмерных векторов, образующих уже не двумерное, а трехмерное линейное пространство. А раз мы говорим о линейном пространстве, то в нем необходимо ввести базис — тройку единичных векторов i, j и k, направленных соответственно вдоль координатных осей ОХ, ОY и OZ. Координаты базисных векторов записываются в виде (1;0;0), (0;1;0) и (0;0;1). Если вспомнить еще и о том, что выбирается ортогональная система координат, т.е. оси взаимно перпендикулярны, а базисные векторы по модулю равны 1, то их принято именовать ортами координатных осей. Напомним также и о том, что любой вектор в трехмерном пространстве может быть выражен через орты с помощью введенных алгебраических операций.

Коллинеарность векторов вводится также аналогично плоскому случаю.

Как видим, для введения коллинеарности понадобился направляющий вектор прямой. Это понятие снова полностью переносится в трехмерное пространство из плоскости с учетом прибавившейся координаты. Соответственно записывается и параметрическое уравнение прямой.

Очевидно, что координатное параметрическое уравнение прямой фактически представляет собой три уравнения, которые можно записать по отдельности для каждой координаты и тем самым после записи параметрического уравнения в координатах оно распадается на три параметрических уравнения для каждой их координат.

Аналогично двумерному случаю вводится и скалярное произведение — метрика линейного пространства векторов.

Любые два свободных неколлинеарных вектора в пространстве определяют некоторую плоскость. Помещая их начала в одной точке, можно построить соответствующий параллелограмм, лежащий также в этой плоскости. Фактически мы при этом привязываемся к плоскости, определяемой данными векторами (часто применяют несколько жаргонное выражение: плоскости, «натянутой» на данные векторы). Очевидно, что площадь этого параллелограмма можно найти по формуле, взятой из плоского случая:

S _ab = |a|·|b|· sinφ

где |a,·|b| — модули данных векторов, φ — угол между ними.

Но здесь необходимо подчеркнуть появляющееся отличие от двумерной геометрии: ведь натянутая на данные векторы плоскость может быть различным образом ориентирована относительно координатных плоскостей.

Теперь перейдем к принципиально отличным от двумерного случая понятиям. Наиболее характерное из них — векторное произведение.

Введенное понятие векторного произведения существенным образом меняет представление о векторе. В самом деле, определение положительного направления для вектора с означает, что векторы a,b,c образуют правую тройку. Более доступным представлением о правой тройке можно считать «правило буравчика»: если производить вращение буравчика (правого винта) по направлению от вектора a к вектору b, то перемещение буравчика покажет направление вектора с.

Иногда, опять же в жаргонном выражении, «правило буравчика» заменяют на «правило штопора», имея в виду, что для буравчика требуется пояснение «правый винт», который вообще может оказаться и левым, а штопоры все правые, поэтому пояснения не требуется.

Но если говорить серьезно, то возможность превращения правой тройки в левую имеет место при зеркальном преобразовании системы координат. В этом случае векторное произведение не остается неизменным, а меняет знак. Имеем принципиальное отличие от «нормальных» векторов общего вида, не меняющих знака при любых преобразованиях координат. Это на первый взгляд несущественное отличие на самом деле оказывается весьма существенным при расширении представлений о линейных пространствах, поэтому для векторного произведения существует специальное наименование «псевдовектор». Если не рассматривать «зеркальные» преобразования координат, то отмеченным различием можно пренебречь. Но забывать о нем вообще не следует.

Еще одним отличным от двумерной геометрии понятием является смешанное произведение трех векторов.

Введенное понятие компланарности векторов также не имеет аналогов в двумерной геометрии.

Вооружившись такими полезными понятиями, можно теперь записать общее уравнение плоскости в пространстве и рассмотреть различные виды записи уравнения плоскости в пространстве, по аналогии с различными записями уравнения прямой на плоскости.

Пусть плоскость проходит через заданную точку М₀ (x₀; y₀; z₀). Потребуем, чтобы она была перпендикулярна данному вектору n = (A;B;C), который назовем вектором нормали к плоскости или просто нормальным вектором. Это значит, что для произвольной точки М (x; y; z), принадлежащей плоскости, вектор М₀М, целиком расположенный в ней, должен давать нулевое скалярное произведение с вектором нормали:

(n, M₀M) = 0

Это уравнение и будет векторным уравнением плоскости в пространстве.

Выражая это скалярное произведение через координаты векторов n и М₀М, получим:

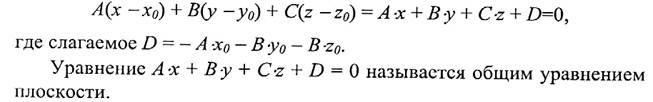Общее уравнение плоскости нетрудно преобразовать к виду, подобному тому, который мы придавали кривым второго порядка (в правой части уравнения стоит 1). Такой вид уравнения называют каноническим, или уравнением плоскости в отрезках.

Вспоминая евклидову геометрию: через три точки в пространстве всегда можно провести единственную плоскость. Переведем этот постулат на язык аналитической геометрии.

Тем самым уравнение плоскости, проходящей через три заданных точки, представляет собой условие компланарности трех векторов М₁М, М₁М₂ и М₁М₃.

Условие компланарности позволяет с успехом записать и уравнение плоскости, содержащей два заданных вектора и заданную точку.

Опираясь на свойства скалярного произведения, можно изящным образом определить расстояние от любой точки в пространстве до данной плоскости, зная, что оно определяется по перпендикуляру к этой плоскости.

Изящество записи параметрического уравнения прямой и сходство формы этого уравнения с параметрическим уравнением прямой на плоскости подталкивает к представлению в параметрическом виде прямой, задаваемой пересечением двух плоскостей. Предварительно отметим, что трехмерное линейное пространство часто обозначается символом R₃.

Тогда, полагая z = t, получим параметрические уравнения прямой, определяемой пересечением двух плоскостей. При этом коэффициенты при параметре t являются координатами направляющего вектора прямой a = (a₁;a₂;a₃):

Наконец, вспомним (опять же из евклидовой геометрии), что точка в пространстве может быть определена как результат пересечения трех непараллельных друг другу плоскостей. Переведем и этот факт на язык аналитической геометрии.

Что у нас в итоге получилось?

Вроде бы мы искали точку пересечения трех плоскостей. Она характеризуется своими координатами (x;y;z). Но из решения геометрической задачи мы получили универсальный способ решения системы трех линейных уравнений с тремя неизвестными:

Полученное правило Крамера дает весьма изящный пример того, как применение методов аналитической геометрии приносит ощутимую пользу алгебре. Завершаем, тем самым, нашу лекцию напоминанием блестящей идеи Рене Декарта, высказанной в далеком XVII веке: анализ геометрических образов можно истолковать на языке алгебраических формул.

Дата добавления: 2014-01-03