Сложение гармонических колебаний

Материальная точка может одновременно участвовать в несколь­ких колебаниях. В этом случае, чтобы найти уравнение и траекто­рию результирующего движения, следует сложить колебания. Наи­более просто выполняется сложение гармонических колебаний. Рас­смотрим две такие задачи.

Сложение гармонических колебаний, направленных по одной прямой. Пусть материальная точка одновременно участву­ет в двух колебаниях, происходящих вдоль одной линии. Анали­тически такие колебания выражаются следующими уравнениями:

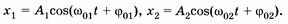
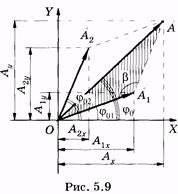
Допустим, что частоты скла­дываемых колебаний одинаковы 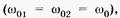тогда результи­рующее смещение точки

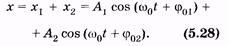
Выполним такое сложение с по­мощью векторной диаграммы. Изо­бразим положение векторов 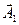и 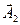в начальный момент времени (рис. 5.9), углы между этими век­торами и осью ОХ равны начальным фазам слагаемых колебаний j₀₁ и j₀₂. Вектор 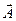— амплитуда результирующего колебания. Так как 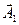и 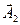вращаются с одинаковой угловой скоростью, то и сумма их — вектор 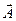— будет вращаться с той же угловой скоро­стью, т. е. результирующее движение является гармоническим с круговой частотой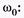

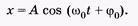(5.29)

Выразим амплитуду А этого колебания и начальную фазу j₁ через заданные значения 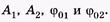Применяя теорему косинусов к треугольнику, заштрихованному на рис. 5.9, получаем

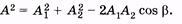
Так как –cos b = -cos [p - (j₀₂ - j₀₁)] = cos (j₀₂ - j₀₁), то

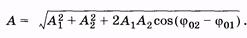(5.30)

Как видно из рис. 5.9, tg j равен отношению проекции 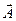на ось OY к проекции 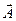на ось ОХ, т. е. А_у /А_х. Учитывая, что проек­ция суммы равна сумме проекций, имеем

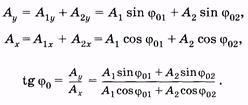(5.31)

Таким образом, поставленная задача решена: по формулам (5.30) и (5.31) можно найти амплитуду и начальную фазу резуль­тирующего колебания. Из выражения (5.30) вытекают следую­щие частные случаи:

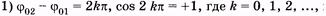
и тогда

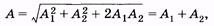
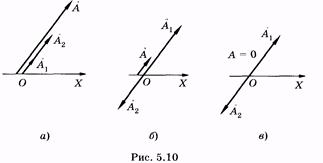
т. е. амплитуда результирующего колебания равна сумме ампли­туд слагаемых колебаний, если разность начальных фаз равна четному числу p (рис. 5.10, а);

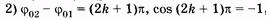
тогда

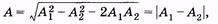
т. е. амплитуда результирующего колебания равна разности амп­литуд слагаемых колебаний, если разность начальных фаз равна нечетному числу p (рис. 5.10, б). В частности, при A₁ = A₂ имеем А = О, т. е. колебания нет (рис. 5.10, в). Это достаточно очевидно: если материальная точка участвует одновременно в двух колеба­ниях, имеющих одинаковую амплитуду и совершающихся в противофазе, то точка неподвижна. Если частоты складываемых ко­лебаний не одинаковы, то сложное колебание уже не будет гармо­ническим.

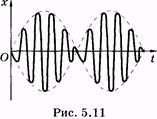Интересен случай, когда частоты слагаемых колебаний мало отличают­ся друг от друга: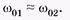

Результирующее колебание при этом подобно гармоническому, но с медлен­но изменяющейся амплитудой (ампли­тудная модуляция). Такие колебания называются биениями (рис. 5.11).

Сложение взаимно перпендикулярных гармонических колебаний. Пусть материальная точка одновременно участвует в двух колебаниях: одно направлено вдоль оси ОХ, другое — вдоль оси OY. Колебания заданы следующими уравнениями:

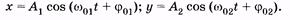(5.34)

Допустим, что частоты колебаний одинаковы, т. е.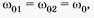тогда

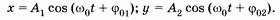(5.35)

Уравнения (5.35) задают траекторию движения материальной точки в параметрической форме. Если в эти уравнения подставлять разные значения t, то можно определить координаты х и у, а сово­купность координат и есть траектория. Более наглядно траекторию можно представить в виде зависимости у = f(x), для получения ко­торой следует исключить время из уравнений (5.35). Произведя ма­тематические преобразования, получим уравнение эллипса:

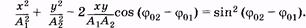(5.36)

Таким образом, при одновременном участии в двух взаим­но перпендикулярных гармонических колебаниях одинаковой частоты материальная точка движется по эллиптической траектории (рис. 5.12).

Из выражения (5.36)вытекают некоторые частные случаи:

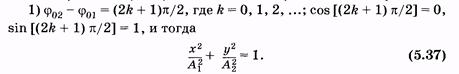
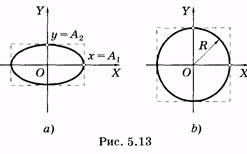
Это каноническая форма уравнения эллипса, соответствующая симметричному расположению его относительно осей координат (рис. 5.13, а). Из (5.37) при А₁ = А₂ = R (рис. 5.13, б) получаем уравнение окружности радиусом R:

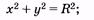(5.38)

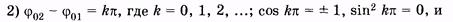
тогда

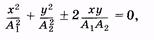(5.39)

и после преобразований

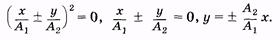(5.40)

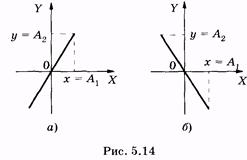
Это уравнение прямой линии, в которую вырождается эллипс [рис. 5.14, а соответствует знаку «+» в уравнении (5.40); рис. 5.14, б — знаку «-»].

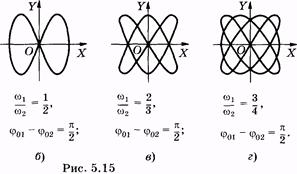
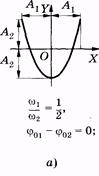
При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу.

Вид фигур Лиссажу зависит как от соотношения амплитуд А₁ и А₂, так и от отношения частот w₁/w₂ и разности начальных фаз j₀₁ - j ₀₂ слагаемых колебаний (рис. 5.15):

Дата добавления: 2014-01-03