Способы описания погрешности и неопределенности с вероятностно-статистических позиций

Целью измерения является получение оценки истинного значения измеряемой величины. Понятие погрешности измерений, как разности между результатом измерений и истинным (действительным) значением измеряемой величины, используется для описания точности измерений в отечественной нормативной документации. Говоря об оценивании погрешности, в отечественной метрологической практике подразумевают оценивание ее характеристик.

Однако, в международной практике общепринятые оценки среднеквадратического отклонения, неисключенной систематической погрешности и доверительных границ множества погрешностей результатов измерений уже не соответствуют исходному определению погрешности. В частности это выражается в некорректном применении понятия «погрешность» при оценке ее характеристик, поскольку они характеризуют не погрешность, а разброс значений, приписываемых измеряемой величине на основе используемой информации, т.е. неопределенность.

С этой целью в «Руководстве по выражению неопределенности измерения» (GUM) вводят понятие «неопределенность измерений». Неопределенность измерений понимают как неполное знание значения измеряемой величины и для количественного выражения этой неполноты вводят распределение вероятностей возможных (обоснованно приписанных) значений измеряемой величины. Таким образом, параметр этого распределения (неопределенность) количественно характеризует точность результата измерений [98].

Сходными для обоих подходов является последовательность действий при оценивании характеристик погрешности и вычислении неопределенности измерений:

- анализ уравнения измерений;

- выявление всех источников возникновения погрешности (неопределенности) измерений и их количественное оценивание;

- введение поправок на систематические погрешности (эффекты), которые можно исключить.

Методы вычисления неопределенности, как и методы оценивания характеристик погрешности, заимствованы из математической статистики, однако при этом используются различные интерпретации закона распределения вероятностей случайной величины.

Систематическая погрешность Dс – разность между математическим ожиданием 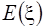результатов наблюдения измеряемой величины ξ и опорным (истинным) значением :

,

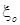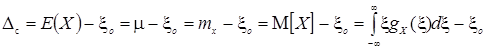где 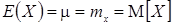– математическое ожидание (различные обозначения одной и той же величины, встречающиеся в технической литературе по метрологии);

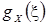– функция распределения случайной величины ξ.

Систематическая погрешность – разность между средним значением, получаемым при бесконечном числе измерений одной и той же измеряемой величины в условиях сходимости, и истинным значением измеряемой величины [62].

Случайная погрешность 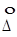– разность между результатом единичного наблюдения и математическим ожиданием результата измерения:

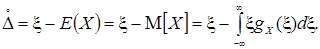
Случайная погрешность – разность результата измерения и среднего значения, которое могло бы быть получено при бесконечно большом числе повторных измерений одной и той же измеряемой величины, проводимых в условиях сходимости [62].

Математическое ожидание погрешности 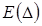равно математическому ожиданию систематической погрешности (составляющей), так как математическое ожидание случайной погрешности всегда равно нулю:

.

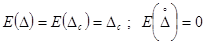Промахом, или грубой погрешностью, называется погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Поскольку грубые погрешности относятся к случайным, для их выявления и исключения применяют методы теории вероятности и математической статистики.

Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения в i -м опыте окажется меньшим некоторого текущего значения Х, от самой величины ξ:

.

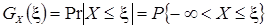Латинская буква Рr является здесь символом вероятности события. Интегральная функция распределения результатов наблюдений является неубывающей функцией аргумента и определена в диапазоне

.

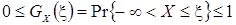Обычно график интегральной функции распределения результатов наблюдений представляет собой непрерывную неубывающую кривую, начинающуюся от нуля на отрицательной бесконечности и асимптотически приближающуюся к единице при увеличении аргумента до плюс бесконечности.

Случайную погрешность Δ тоже следует рассматривать как случайную величину, принимающую в разных опытах различные значения Δ _i. Ее интегральную функцию распределения получаем переносом начала координат в точку ξ = Q, где Q – истинное значение измеряемой величины:

.

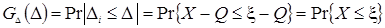В некоторых случаях более удобным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей и обозначаемой через g_Х (ξ). Иногда используется обозначение G_Х (ξ). Дифференциальная функция распределения является функцией, производной от интегральной по своему аргументу:

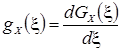. (3.1)

Здесь и далее плотность и функция распределения вероятности будут обозначаться как g и G соответственно в разрез общепринятому обозначению как f и F в связи с использованием f для описания функции измерения. Используемые в обозначениях индексы соответствуют случайной величине.

График дифференциальной функции распределения, который называют кривой распределения, чаще всего имеет колоколообразную форму и обладает максимумом при ξ = Q.

От дифференциальной функции распределения легко перейти к интегральной путем интегрирования первой

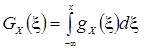. (3.2)

Поскольку 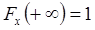, то справедливо следующее равенство:

.

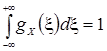Для интегральной функции распределения справедливо следующее утверждение: вероятность попадания результата наблюдений в заданный интервал равна разности значений функции распределения на границах этого интервала т.е.

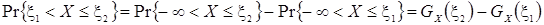
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают в исключительных случаях, а используют специальные величины.

Начальным моментом r -го порядка результатов наблюдений называется интеграл вида

,

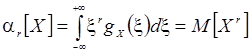представляющий собой математическое ожидание степени 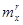. Откуда следует, что первый начальный момент совпадает с математическим ожиданием результатов наблюдений: .

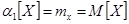Математическое ожидание случайной величины х 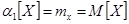называют также ожидаемым значением или средним значением [8]. Ее оценкой является среднее арифметическое значение из n независимых наблюдений случайной величины х, плотность распределения вероятностей которой :

.

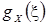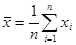Центральным моментом r -го порядка результатов наблюдений называется интеграл вида

,

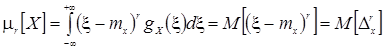представляющий собой математическое ожидание величины 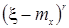, т. е. r -й степени случайной погрешности .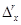

Можно показать, что первый центральный момент результатов наблюдений тождественно равен нулю.

.

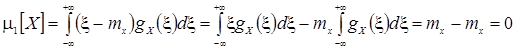Начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений: 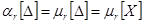, поскольку математическое ожидание случайных погрешностей равно нулю.

Вычислим второй центральный момент, называемый дисперсией результатов наблюдений и обозначаемый через :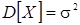

,

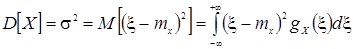Оценку дисперсии можно получить по формуле:

.

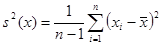Множитель 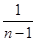в выражении для 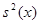обусловлен корреляцией между 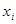и 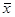и отражает тот факт, что среди слагаемых 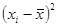есть только 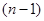независимых членов.

Если математическое ожидание 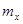случайной величины х известно, то оценку дисперсии получают по формуле:

.

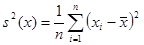Надлежащей мерой неопределенности результата измерения является не дисперсия наблюдаемой величины, а дисперсия среднего арифметического по выборке наблюдений. Необходимо четко различать дисперсию случайной величины 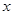и дисперсию ее среднего арифметического значения 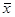. Дисперсия среднего арифметического по ряду наблюдений из n независимых наблюдений 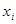определяется как:

.

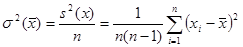Однако размерность дисперсии выражается в единицах величины в квадрате. Поэтому в качестве числовой характеристики точности измерений используют стандартное отклонение (среднеквадратическое отклонение СКО, среднеквадратическая погрешность, СКП):

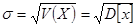
с положительным знаком и выражаемое в единицах погрешности (и, естественно, совпадающей с единицей измеряемой физической величины).

В соответствии с «Руководством по выражению неопределенности измерений» стандартные неопределенности входных величин выражаются в виде стандартных отклонений и находятся статистическими и нестатистическими методами, получая, соответственно, стандартные неопределенности типа А (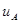) или стандартные неопределенности В ().

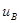Сопоставление оценок характеристик погрешностей и неопределенностей измерений приведено на рис. 3.1.

Стандартная неопределенность измерения типа А i -й входной величины находится по формуле:

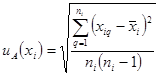. (3.3)

Она соответствует стандартному отклонению (СКО) результата измерения (среднего арифметического) i -й входной величины.

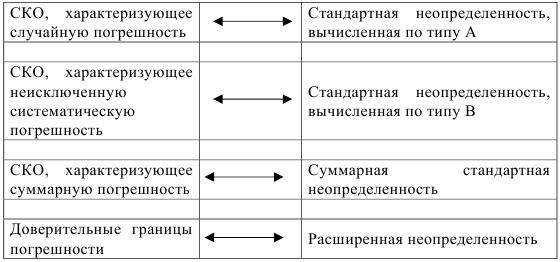
Рис. 3.1. Сопоставление оценок двух подходов к оценке точности измерений

Стандартная неопределенность типа В i- й входной величины находится в зависимости от априорной информации об изменчивости входной величины (табл. 3.1).

Таблица 3.1

Дата добавления: 2014-01-03