
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление стандартной неопределенности типа В входных величин
|
|
|
|
| № п/п | Априорная информация об изменчивости входной величины | Оценка стандартной неопределенности типа В |
Известно стандартное отклонение i -й входной величины 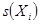
| Принимается равной известному стандартному отклонению
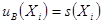
| |
Известны ранее выполненные результаты многократных наблюдений i-й входной величины 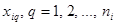
| Вычисляется стандартное отклонение
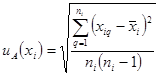 , где , где 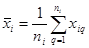
| |
Можно оценить лишь верхнюю и нижнюю границы входной величины 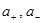 , причем , причем 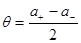
| Вычисляется по формуле: 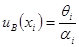 ,
где ,
где 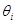 – границы i -й составляющей неисключен-ной систематической погрешности (НСП); – границы i -й составляющей неисключен-ной систематической погрешности (НСП);
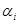 – коэффициент, соответствующий принимае-мому закону распределения внутри границ – коэффициент, соответствующий принимае-мому закону распределения внутри границ 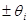 НСП; для равномерного (или неизвестного) закона распределения НСП; для равномерного (или неизвестного) закона распределения 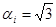 ; для треугольного закона распределения ; для треугольного закона распределения 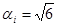 ; для закона арксинуса ; для закона арксинуса 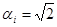 и т.д. и т.д.
| |
Известны интервалы 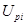 с уровнем доверия р с уровнем доверия р
| В предположении нормального закона распреде-ления определяется как 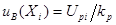 , где , где 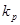 – коэффициент охвата для нормального распределения, равный соответственно 1,64; 1,96 и 2,58 для уровня доверия р = 0,9; 0,95 и 0,99. – коэффициент охвата для нормального распределения, равный соответственно 1,64; 1,96 и 2,58 для уровня доверия р = 0,9; 0,95 и 0,99.
|
Стандартную неопределенность оценки (результата измерения) y измеряемой величины Y получают путем соответствующего определенного суммирования стандартных неопределенностей входных оценок 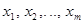 . Эту суммарную стандартную неопределенность оценки y обозначают как
. Эту суммарную стандартную неопределенность оценки y обозначают как 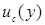 .
.
Определение стандартной неопределенности выходной величины (суммарной стандартной неопределенности) осуществляется по формулам, называемым законом распределения неопределенности.
При отсутствии корреляций между входными величинами стандартная неопределенность выходной величины определяется как:
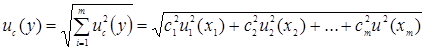 , (3.4)
, (3.4)
где 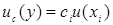 – суммарную неопределенность, определяемая как произведение коэффициента чувствительности
– суммарную неопределенность, определяемая как произведение коэффициента чувствительности 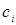 на неопределенность входной величины;
на неопределенность входной величины;
|
|
|
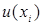 – стандартная неопределенность входной величины, оцененная по типу А или В.
– стандартная неопределенность входной величины, оцененная по типу А или В.
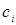 – коэффициенты чувствительности, которые показывают, как оценка выходной величины y изменяется с изменением оценок входных величин
– коэффициенты чувствительности, которые показывают, как оценка выходной величины y изменяется с изменением оценок входных величин 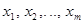 :
:
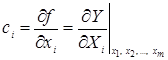 (3.5)
(3.5)
При прямых измерениях все коэффициенты чувствительности равны 1.
При наличии корреляций между входными величинами стандартная неопределенность выходной величины определяется как:
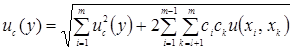 . (3.6)
. (3.6)
Для оценивания неопределенности выходной величины при наличии корреляций коррелированные величины объединяются в единый блок. Тогда для каждого такого блока можно оценить его вклад неопределенности (например, 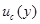 ) в неопределенность выходной величины
) в неопределенность выходной величины 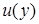 , их число степеней свободы (
, их число степеней свободы (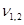 ) и закон распределения. Число степеней свободы для вклада неопределенности с корреляцией, оцененной по типу А, будет равно (n – 1), а для типа В – бесконечности. При равенстве коэффициента корреляции блока ±1 его вклад неопределенности оценивается как:
) и закон распределения. Число степеней свободы для вклада неопределенности с корреляцией, оцененной по типу А, будет равно (n – 1), а для типа В – бесконечности. При равенстве коэффициента корреляции блока ±1 его вклад неопределенности оценивается как:
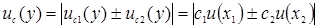 . (3.7)
. (3.7)
Суммарная стандартная неопределенность 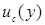 представляет собой оценку стандартного отклонения измеряемой величины Y и характеризует разброс значений, которые с достаточным основанием могут быть приписаны измеряемой величине.
представляет собой оценку стандартного отклонения измеряемой величины Y и характеризует разброс значений, которые с достаточным основанием могут быть приписаны измеряемой величине.
Дополнительной мерой неопределенности, которая удовлетворяет требованию представления интервала, является расширенная неопределенность, обозначаемая символом U. Ее получают путем умножения неопределенности выходной величины (суммарной стандартной неопределенности) на коэффициент охвата k:
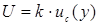 (3.8)
(3.8)
При этом результат измерения удобно выражать в виде: 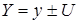 , обозначающем, что лучшей оценкой значения, приписываемого измеряемой величине Y, является y и что интервал от y – U до y + U содержит, как можно ожидать, большую часть распределения значений, которые можно с достаточным основанием приписать Y. Другой формой записи такого интервала будет
, обозначающем, что лучшей оценкой значения, приписываемого измеряемой величине Y, является y и что интервал от y – U до y + U содержит, как можно ожидать, большую часть распределения значений, которые можно с достаточным основанием приписать Y. Другой формой записи такого интервала будет 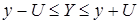 .
.
|
|
|
Термины «доверительный интервал» и «доверительная вероятность», нашедшие применение в математической статистике и имеющие точную формулировку, могут быть применены к интервалу, определяемому через U, только при выполнении определенных условий. В частности, все составляющие неопределенности, входящие в 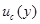 , должны представлять собой оценки по типу А. Поэтому в Руководстве прилагательное «доверительный» применительно к интервалу, определяемому через U, к вероятности нахождения измеряемой величины внутри этого интервала не используется. Вместо «доверительной вероятности» используется термин «уровень доверия». Более точно, U понимается как параметр, характеризующий интервал, в который попадает результат измерения и который содержит большую часть p распределения вероятностей, связанного с результатом измерения и его суммарной стандартной неопределенностью. При этом p является вероятностью охвата или уровнем доверия для этого интервала [8].
, должны представлять собой оценки по типу А. Поэтому в Руководстве прилагательное «доверительный» применительно к интервалу, определяемому через U, к вероятности нахождения измеряемой величины внутри этого интервала не используется. Вместо «доверительной вероятности» используется термин «уровень доверия». Более точно, U понимается как параметр, характеризующий интервал, в который попадает результат измерения и который содержит большую часть p распределения вероятностей, связанного с результатом измерения и его суммарной стандартной неопределенностью. При этом p является вероятностью охвата или уровнем доверия для этого интервала [8].
В практике измерений применяют различные значения уровня доверия, например: 0,90; 0,95; 0,98; 0,99; 0,9973, 0,999 и даже выше, когда связано с безопасностью и здоровьем людей. В настоящее время в нормативных документах, если нет веских оснований, рекомендовано принимать уровень доверия, равный 0,95 для обычной практики измерений и 0,99 для точных измерений или в случае, когда измерения нельзя повторить.
Значение коэффициента k выбирают на основе уровня доверия, требуемого для интервала y – U до y + U. Обычно k принимает значения от 2 до 3, однако в особых случаях значение k может находиться вне этих границ. Определить значение k, отвечающему выбранному уровню доверия, не всегда легко реализовать на практике, поскольку требует точного знания вида закона распределения вероятностей, характеризуемого результатом измерения y и его суммарной стандартной неопределенностью 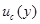 . Часто на практике принимают значение k = 2, соответствующему интервалу с уровнем доверия, близким к 95%, k = 3 – интервалу с уровнем доверия, близким к 99%.
. Часто на практике принимают значение k = 2, соответствующему интервалу с уровнем доверия, близким к 95%, k = 3 – интервалу с уровнем доверия, близким к 99%.
Для представления результата измерения следует:
а) ясно описать методы, использованные для получения результата измерения и его неопределенности из экспериментальных наблюдений и иной доступной информации;
|
|
|
б) перечислить все составляющие неопределенности и подробно описать, как они были оценены;
в) представить анализ данных таким образом, чтобы можно было легко проследить все этапы вычислений и, при необходимости, их повторить;
г) указать все поправки и константы, использованные при анализе, и указать источники их получения.
Так, в соответствии с Руководством ИСО/МЭК 98-3:2008, требования которого отражены в ГОСТ Р 54500.3-2011, установлено следующие частные рекомендации представления результатов оценивания неопределенности. Если мерой неопределенности результата измерения является суммарная стандартная неопределенность 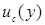 , то при представлении результата измерения следует:
, то при представлении результата измерения следует:
а) дать подробное определение измеряемой величины Y;
б) привести оценку y измеряемой величины Y и суммарной стандартной неопределенности 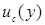 с указанием единиц измерений;
с указанием единиц измерений;
в) при необходимости указать относительную суммарную стандартную неопределенность 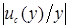 ,
, 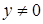 ;
;
г) значение каждой входной оценки 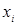 и ее стандартной неопределен-ности
и ее стандартной неопределен-ности 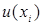 , а также, как они были получены;
, а также, как они были получены;
д) оценки ковариаций или коэффициентов корреляции для всех коррелированных входных величин, а также методы, использованные для получения этих оценок;
е) число степеней свободы для стандартной неопределенности каждой входной оценки;
ж) функциональную зависимость 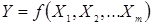 , а также при необходимости могут быть приведены частные производные (коэффициенты чувствительности)
, а также при необходимости могут быть приведены частные производные (коэффициенты чувствительности) 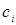 .
.
При этом предпочтительно во избежание разночтений использовать одну из четырех форм записи результатов измерения (например, измеряемой величиной является масса эталона 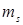 с номинальным значением 100 г):
с номинальным значением 100 г):
а) 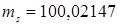 г (суммарная стандартная неопределенность);
г (суммарная стандартная неопределенность); 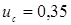 мг;
мг;
б) 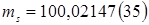 г, где число в скобках – суммарная стандартная неопределенность
г, где число в скобках – суммарная стандартная неопределенность 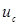 двух младших разрядов результата измерения;
двух младших разрядов результата измерения;
в) 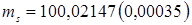 г, где число в скобках – суммарная стандартная неопределенность
г, где число в скобках – суммарная стандартная неопределенность 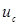 в тех же единицах измерения (г);
в тех же единицах измерения (г);
г) 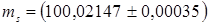 г, где число, стоящее после знака «±» – суммарная стандартная неопределенность
г, где число, стоящее после знака «±» – суммарная стандартная неопределенность 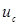 , а не доверительный интервал.
, а не доверительный интервал.
|
|
|
Представления с использованием знака «±» следует по возможности избегать, поскольку его традиционно используют для указания интервала, соответствующему некоторому высокому уровню доверия, и поэтому, число, следующее за этим знаком, легко спутать с расширенной неопределен-ностью. Так, например, запись 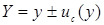 может быть интерпретирована как указание расширенной неопределенности с коэффициентом охвата k = 1 или интервала
может быть интерпретирована как указание расширенной неопределенности с коэффициентом охвата k = 1 или интервала 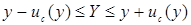 с определенным уровнем доверия p.
с определенным уровнем доверия p.
Если мерой неопределенности является расширенная неопределенность 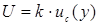 , то при представлении результата измерения следует:
, то при представлении результата измерения следует:
а) дать подробное определение измеряемой величины Y;
б) указать результат измерения в виде 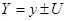 с указанием единиц измерений для y и U;
с указанием единиц измерений для y и U;
в) при необходимости указать относительную расширенную неопределенность 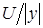 ,
, 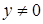 ;
;
г) указать использованное для получения расширенной неопределен-ности значение k;
д) указать приблизительный уровень доверия для интервала 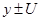 и пояснить, как он был определен;
и пояснить, как он был определен;
е) оценки ковариаций или коэффициентов корреляции для всех коррелированных входных величин, а также методы, использованные для получения этих оценок;
ж) число степеней свободы для стандартной неопределенности каждой входной оценки;
з) функциональную зависимость 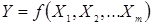 , а также при необходимости могут быть приведены частные производные (коэффициенты чувствительности)
, а также при необходимости могут быть приведены частные производные (коэффициенты чувствительности) 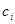 .
.
При этом предпочтительно использовать следующую запись: 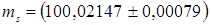 г, где число, стоящее после знака «±» расширенная неопределенность
г, где число, стоящее после знака «±» расширенная неопределенность 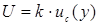 , полученная для суммарной стандартной неопределенности
, полученная для суммарной стандартной неопределенности 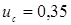 мг и коэффициент охвата k = 2,26, соответствующего уровню доверия 95% для t -распределения с
мг и коэффициент охвата k = 2,26, соответствующего уровню доверия 95% для t -распределения с 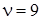 степенями свободы.
степенями свободы.
Любая из форм представления результата измерения должна содержать необходимые данные, на основании которых может быть определена расширенная неопределенность для лучшей оценки значения, приписываемого измеряемой величине. В общем случае расширенная неопределенность может быть установлена, если известен вид закона распределения и основные числовые характеристики этого закона.
На рис. 3.1 а и 3.1 б графически схематично изображены погрешности измерений классическим способом и с учетом «Руководства по выражению неопределенности измерений».
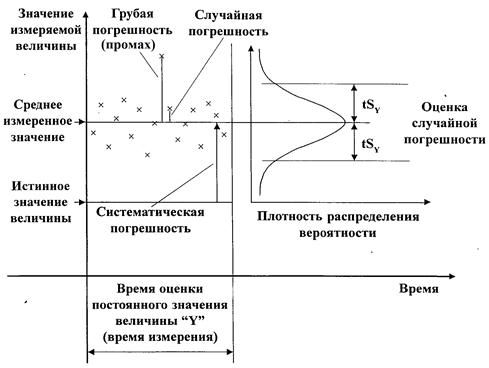
а
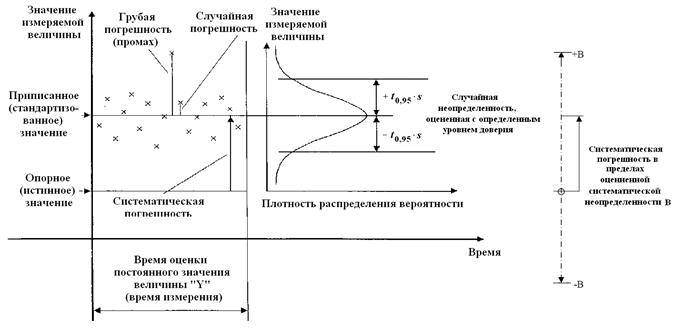
б
Рис. 3.1. Погрешности измерений
Наряду с названными понятиями в метрологической практике используются ряд других понятий, связанных с качеством измерительного процесса:
Точность измерений – одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Правильность – степень близости результата измерений к истинному (действительному) значению измеряемой величины.
Показателем правильности является отсутствие или малая величина систематической погрешности, т.е. близость математического ожидания (среднего арифметического значения) к опорной (истинной) величине.
Прецизионность – степень близости друг к другу независимых результатов измерений, полученных в конкретных регламентированных условиях.
Показателем прецизионности является отсутствие или малая величина случайных погрешностей (или их обобщенная характеристика – стандартное отклонение). Прецизионность в бытовом понимании – кучность.
Сходимость результатов измерений (сходимость измерений) – близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.
Воспроизводимость результатов измерений (сходимость измерений) – близость результатов измерений одной и той же величины, полученных в различных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений (температуре, давлению, влажности и т.д.).
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 3566; Нарушение авторских прав?; Мы поможем в написании вашей работы!