Непрерывность функции в точке

Лекция № 4

Тема: «Непрерывность функции»

1.Непрерывность функции в точке 2. Классификация точек разрыва. 3. Действия над непрерывными функциями. 4. Теорема о непрерывности сложной функции 5. Свойства функций, непрерывных на отрезке  

Понятие непрерывности является одним из основных понятий математического анализа.

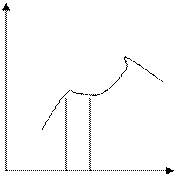
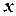
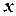
Сигнал – непрерывный, случайный процесс. Говоря о непрерывности, мы представляем себе плавную, нигде не прерывающуюся кривую. При рассмотрении графика мы видим, что близким значениям аргумента соответствуют близкие значения функции.

Пусть функция 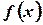определена в некоторой окрестности точкой .

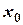О.1.1 Функция 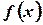называется непрерывной в точке 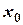, если предел функции при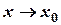равен значению функции в этой точке, т.е.

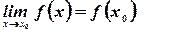(1)

Так как 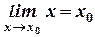, то соотношение 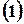можно записать в виде ,

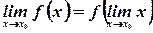т.е. для непрерывной функции можно представить знак функции и знак предела.

Приведем равносильное определение непрерывности функции на языке «».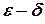

О.1.2 Функция 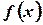называется непрерывной в точке 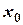, если для любого 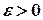, существует 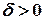, что для всех 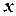удовлетворяющих неравенству 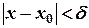, выполняется неравенство . .

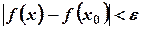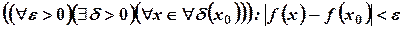Если 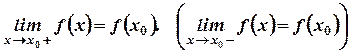, то функцию 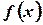называют непрерывной в точке 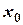справа (слева).

Если функция 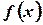непрерывна в точке 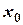слева и справа, то она непрерывна в этой точке. Действительно, в силу теоремы (л.2 «Предел функции в точке») о необходимом и достаточном условии существования предела функции в точке. (Для того чтобы существовал предел функции в точке, необходимо и достаточно существование обоих односторонних пределов функции в точке и их равенство). Предел функции в точке 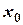равен значению ее в этой точке.

Приведем еще одно определение непрерывности функции, которое является перефразировкой первого определения. Перенесем в равенстве (1) 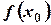в левую часть и внесем 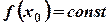под знак предела (теорема о пределах). Так как 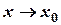равночисленно 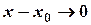, то получим:

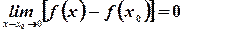(2)

Разность 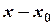, т.е. разность двух значений аргумента, называется приращением аргумента 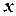в точке 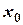и обозначается 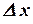, а разность 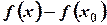- двух значений функции, называется приращением функции в точке 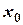и обозначается 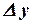. Тогда

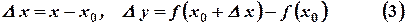
При фиксированной точке 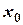, 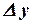является функцией от аргумента 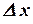, т.е.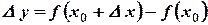

Геометрический смысл ясен из рисунка. Равенство (2) в новых обозначениях примет вид:

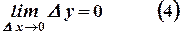
Соотношение (4) и дает нам еще одно определение непрерывной функции.

О.1.3 Функция 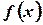называется непрерывной в точке 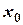, если бесконечно малому приращению аргумента 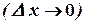соответствует бесконечно малое приращение функции.

Оно удобно для практического использования.

Пример: доказать, что 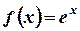- непрерывная функция на всей области определения .

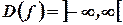Для доказательства возьмем некоторую точку 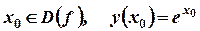, дадим 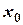приращение 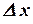, тогда новое значение аргумента 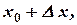а значение функции .

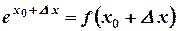Найдем приращение функции.

.

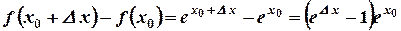Используем предельный переход и четвертый замечательный предел

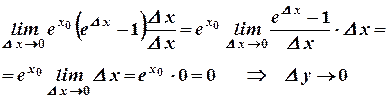
бесконечно малое при .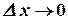

Функция непрерывна в точке 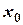, но точка 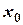- произвольная точка .

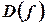О.1.4 Функция 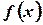называется непрерывной на промежутке 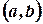, если она непрерывна в каждой точке этого промежутка.

На основании всего сказанного выше, дадим строгое определение непрерывности функции (необходимое и достаточное условия непрерывной функции в точке).

О.1.5 Функция называется непрерывной в точке 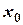, если

1) функция определена в этой точке и некоторой ее окрестности т.е. 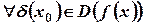(внутренняя точка).

2)

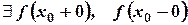
3)

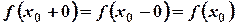
Оказывается, что не для любой функции выполняются условия О.1.5. В этом случае говорят о том, что функция терпит разрыв.

Дата добавления: 2014-01-03