Метод замены плоскостей проекций

ОБЩИЕ ПОЛОЖЕНИЯ

СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА

Лекция 4

Решение ряда задач в начертательной геометрии значительно упрощается, когда геометрические фигуры занимают частное положение относительно плоскостей проекций. Задачи на определение взаимного положения фигур и метрические задачи (определение натуральных величин плоскостей, отрезков и т.д.). Для этого существуют различные способы преобразования комплексного чертежа. Каждый из них основан на одном из следующих принципов:

1. на изменении положения плоскостей проекций относительно неподвижных геометрических фигур;

2. на изменении положения заданных геометрических фигур относительно неподвижных плоскостей проекций;

Рассмотрим некоторые из них.

Сущность способа состоит в том, что заданные геометрические фигуры неподвижны в заданной системе плоскостей проекций (П₁, П₂). Последовательно вводятся новые плоскости проекций (П₄, П₅), относительно которых геометрические фигуры займут частное положение. Новая плоскость проекций выбирается с таким расчетом, чтобы она была перпендикулярной к незаменяемой плоскости проекций.

Большинство задач решается с применением одного или двух последовательных преобразований исходной системы плоскостей проекций. Одновременно можно заменять только одну плоскость проекций П₁ (или П₂), другая плоскость П₂ (или П₁) должна оставаться неизменной.
На рисунке 1 представлено наглядное изображение метода замены плоскостей проекций. Фронтальная плоскость П₂ заменяется на новую фронтальную плоскость П₄. Новые проекции точки А (А₁ А₄), при этом, как видно из рисунка, высота точки А осталась прежней.

Необходимо запомнить правило построения новых проекций точек при методе замены:

1. линии связи всегда перпендикулярны новым осям проекций;
2. расстояние от новой оси проекций до новой проекции точки всегда берется с той плоскости, которую заменяют.

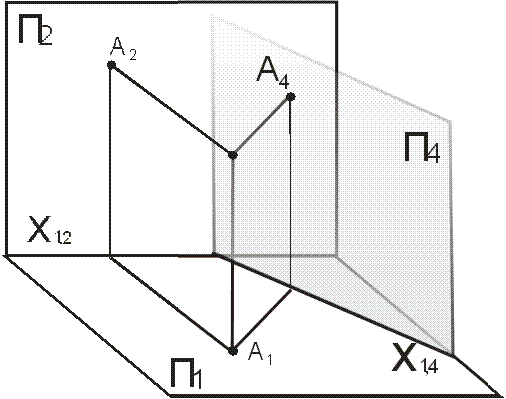
Рисунок 1.Наглядное изображение метода замены плоскостей проекций.

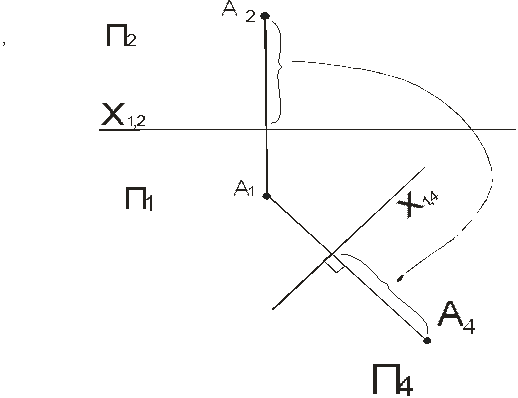
Рисунок 2.Изображение метода замены плоскостей проекций на эпюре.

Большинство задач в начертательной геометрии решаются на базе четырех задач:

1. Преобразовать прямую общего положения в прямую уровня;
2. Преобразовать прямую общего положения в проецирующую прямую;
3. Преобразовать плоскость общего положения в проецирующую плоскость;
4. Преобразовать плоскость общего положения в плоскость уровня.

Задача №1

Рассмотрим решение задачи №1. Дана прямая АВ – общего положения, преобразуем ее в прямую уровня (рис.3). Для этого вводим новую фронтальную плоскость проекций П₄, ось Х_1,4 проводим параллельно А₁В₁. Строим новую проекцию прямой АВ – А₄В_4. В новой системе плоскостей проекций прямая АВ – фронталь.

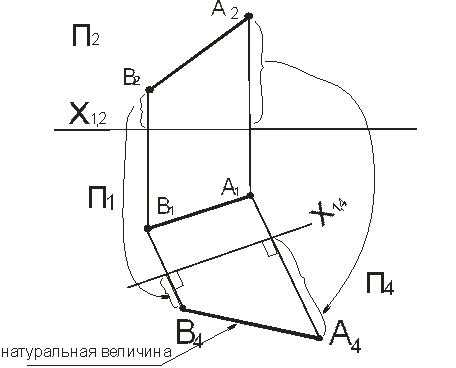
Рисунок 3.

Преобразование прямой общего положения в прямую уровня (фронталь)

Задача №2

Дана прямая АВ – общего положения, преобразуем ее в проецирующую прямую (рис.4). Для решения этой задачи необходимо выполнить последовательно два преобразования:

1. Преобразовать прямую общего положения в прямую уровня, то есть решить сначала задачу №1;
2. Преобразовать прямую уровня в проецирующую прямую.

Вычертить условие задачи №1, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П₅, для этого проводим новую ось проекций Х₄,₅ перпендикулярно проекции А₄В₄ и строим новую проекцию прямой А₅В_5. В системе плоскостей П₄,П₅, прямая АВ является горизонтально проецирующей прямой.

На базе задач №1 и №2 решаются следующие задачи:

1. определение расстояния от точки до прямой;

2. определение расстояния между параллельными и скрещивающимися прямыми;

3. определение натуральной величины прямой;

4. определение величины двугранного угла.

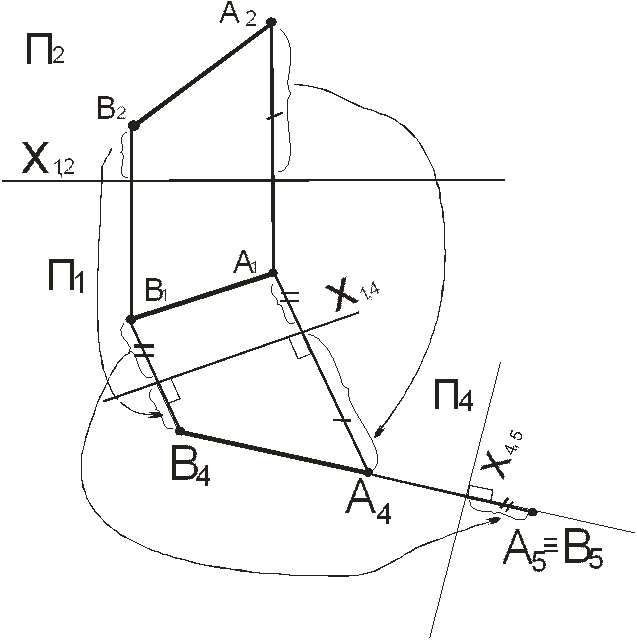
Рисунок 4.

Преобразование прямой общего положения в проецирующую прямую.

Задача №3.

Дана плоскость АВС – общего положения, преобразуем ее в проецирующую плоскость (рис.5). Для решения этой задачи необходимо в плоскости провести линию уровня, если такая отсутствует. Новую ось проекций проводим перпендикулярно лини уровня. В треугольнике АВС проводим горизонталь h. Ось проекций Х₁₄ проводим перпендикулярно h₁, новую проекцию плоскости А₄В₄С₄, строим по правилам, разобранным в предыдущих задачах.

В системе плоскостей проекций П₁,П_4, плоскость треугольника является фронтально-проецирующей плоскостью.

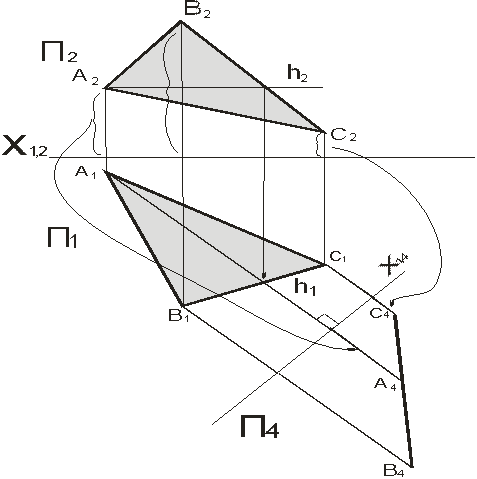
Рисунок 5.

Преобразование плоскости общего положения в проецирующую плоскость.

Задача №4.

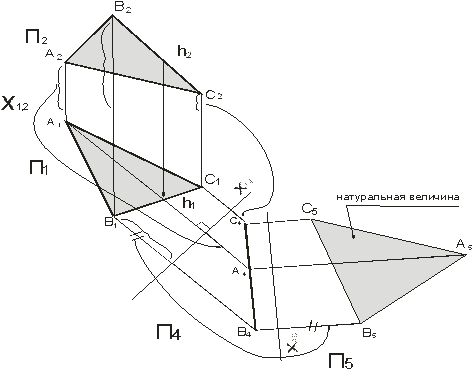
Рисунок 6.

Преобразование плоскости общего положения в плоскость уровня.

Дана плоскость АВС – общего положения, преобразуем ее в плоскость уровня (рис.6). Для решения этой задачи необходимо выполнить последовательно два преобразования:

1. Преобразовать плоскость общего положения в проецирующую плоскость, то есть решить сначала задачу №3;
2. Преобразовать проецирующую плоскость в плоскость уровня.

Вычертить условие задачи №3, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П₅, для этого проводим новую ось проекций Х₄,₅ параллельно проекции А₄В₄С₄ и строим новую проекцию треугольника А₅В₅С_5. В системе плоскостей П₄,П₅, треугольник АВС является горизонтальной плоскостью уровня.

На базе задач №3 и №4 решаются следующие задачи:

1. определение расстояния от точки до плоскости;

2. определение расстояния между параллельными плоскостями;

3. определение натуральных (истинных) величин геометрических фигур;

определение углов наклона плоскости к плоскостям проекций

Метод плоскопараллельного перемещения

Все вышерассмотренные задачи можно решить используя метод плоско-параллельного перемещения, при котором плоскости проекций остаются на месте, а проекция фигуры перемещается (рис.7).

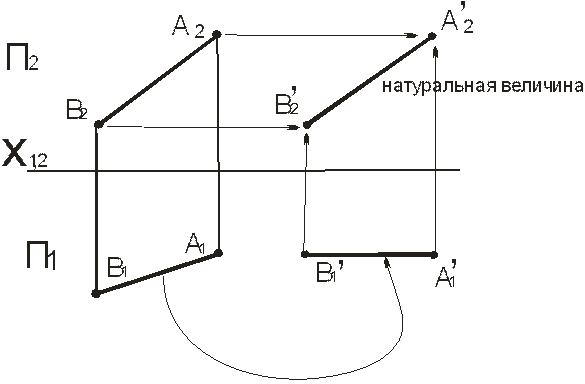
Рисунок 7. Определение натуральной величины отрезка методом плоско-параллельного перемещения.

Дана прямая АВ – общего положения, преобразуем ее в прямую уровня (рис.7). Для этого перемещаем проекцию А₁В₁ параллельно оси Х. Строим новую проекцию прямой АВ – А₂^{`</sup>В<sub>2</sub><sup>`} , которая будетявляться - натуральной величиной отрезка. Этот метод используется для определения натуральных величин ребер многогранников при построении развертки.

Метод вращения

Частным случаем плоско-параллельного перемещения является метод вращения вокруг проецирующих прямых и прямых уровня.

Дата добавления: 2014-01-03