Многогранные поверхности. Многогранники

Лекция 5

Формулировки решения должно быть точными, ясными, лаконичными.

Решение должно предусматривать возможность верификации и контроля исполнения.

Решение должно быть устойчивым по эффективности к возможным ошибкам в определении исходных данных.

Решение должно быть своевременным (оперативным).

Решение должно быть непротиворечивым.

Непротиворечивость означает его согласованность с ранее принятыми решениями.

- Решение должно быть реализуемыми, то есть не содержать положений, которые сорвут исполнение в результате порождаемых им конфликтов.

- Решение должно быть гибким, то есть:

а) изменять цель и (или) алгоритм достижения цели при изменении внешних или внутренних условий,

б) содержать описание состояний объекта управления, внешней среды, при которых выполнение решения должно быть приостановлено и начата разработка нового решения.

Поверхность, образованная частями попарно пересекающихся плоскостей, называется многогранной. На рис. 1 изображены виды многогранных поверхностей. Многогранная поверхность называется пирамидальной, если все ее ребра пересекаются в одной точке - вершине (рис.1, а). Многогранная поверхность называется призматической, если все ее ребра параллельны между собой (рис.1.б).

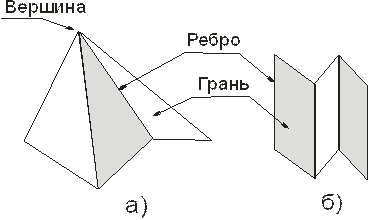
Рис.1. Изображение многогранных поверхностей, а - пирамидальной, б – призматической.

Элементами многогранных поверхностей являются грани, ребра и вершины. Отсеки плоскостей, образующие многогранную поверхность, называются гранями, линии пересечения смежных граней - ребрами, точки пересечения ребер - вершинами.

Геометрическое тело, со всех сторон ограниченное плоскими многоугольниками, называется многогранником. Простейшими многогранниками являются пирамиды и призмы. Среди других видов многогранников следует выделить - призматоиды и правильные многогранники (тела Платона). Призматоидом называется многогранник, у которого верхнее и нижнее основания - многоугольники, расположенные в параллельных плоскостях, а боковые грани представляют собой треугольники или трапеции (рис. 2).

Рисунок 2. Призматоид.

Существует пять правильных многогранников:

1. Тетраэдр (четырехгранник) - ограничен четырьмя равносторонними и равными треугольниками.

1. Гексаэдр (четырехгранник, или куб) - ограничен шестью равными квадратами.
2. Октаэдр (восьмигранник) - ограничен восемью равносторонними и равными треугольниками.
3. Додекаэдр (двенадцатигранник) - ограничен двенадцатью равносторонними и равными пятиугольниками.
4. Икосаэдр (двадцатигранник) - ограничен двадцатью равносторонними и равными треугольниками.

Вокруг всех правильных многогранников можно описать сферу.

Дата добавления: 2014-01-03