Амплитудная модуляция

Амплитудная модуляция - процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

u(t)=Um_u sinΩt (1)

на несущее колебание

S(t)=Um sin(ω₀t+ ω) (2)

происходит изменение амплитуды несущего сигнала по закону:

Uам(t)=Um+а_ам Um_u sinΩt (3)

где а_ам — коэффициент пропорциональности амплитудной модуляции.

Подставив (3) в математическую модель (2) получим:

Sам(t)=(Um+а_ам Um_u sinΩt) sin(ω₀t+ ω). (4)

Вынесем Um за скобки:

Sам(t)=Um(1+а_ам Um_u/Um sinΩt) sin(ω₀t+ ω) (5)

Отношение а_ам Um_u/Um = m_ам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом m_ам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Sам(t)=Um(1+m_ам sinΩt) sin(ω₀t+ ω). (6)

Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:

Sам(t)=(Um+а_ам u(t)) sin(?₀t+?). (7)

Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.

Sам(t)=Um(1+m_ам sin? t) sin(?₀t+?)= Um sin(?₀t+?)+

+m_амUm/2 sin((?₀ -?) t+j) - m_амUm/2 sin((?₀ +?)t+j). (8)

Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте? ₀-? называется нижней боковой составляющей, а на частоте? ₀ +? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).

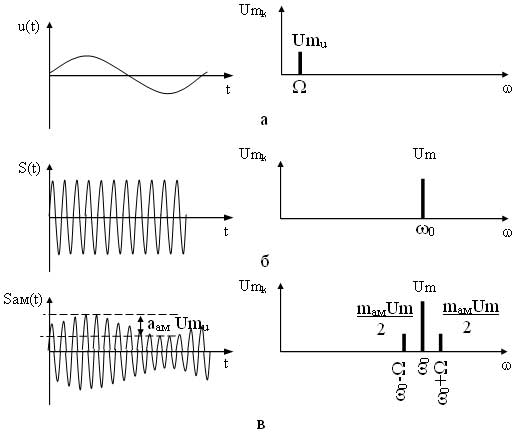
Рисунок 2 - Временные и спектральные диаграммы модулирующего (а), несущего (б) и ампдтудно-модулированного (в) сигналов

Ширина спектра для данного сигнала будет определятся

D?_ам=(?₀+?)-(?₀-?)=2? (9)

Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).

Составляющие в диапазоне частот (ω ₀ — Ω max) и (ω ₀ — Ω min) образуют нижнюю боковую полосу (НБП), а составляющие в диапазоне частот (ω ₀ + Ω min) и (ω ₀ + Ω max) образуют верхнюю боковую полосу (ВБП)

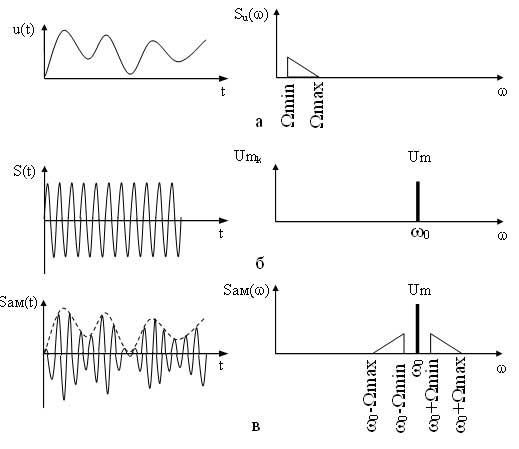
Рисунок 3 - Временные и спектральные диаграммы сигналов при случайном модулирующем сигнале

Ширина спектра для данного сигнала будет определятся

D?_ам=(ω ₀+Ωmax) — (ω ₀ - Ωmin)=2 max (10)

На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах m_ам. Как видно при m_ам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,

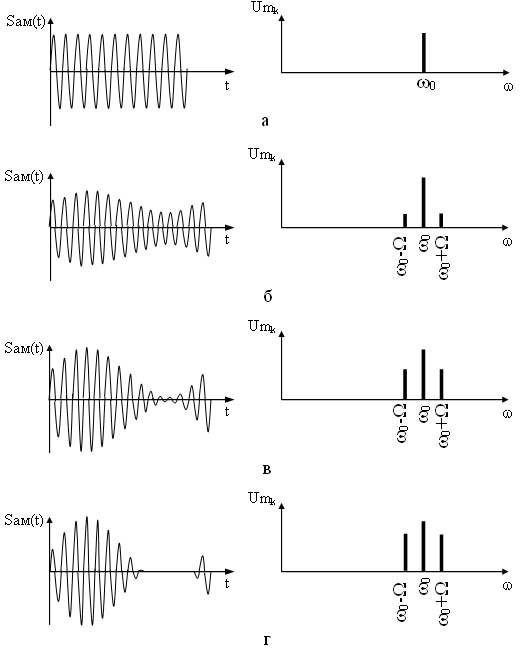
Рисунок 4 - Временные и спектральные диаграммы АМ сигналов при различных mам: а) при mам=0, б) при mам=0,5, в) при mам=1, г) при mам>1

а), при индексе модуляции m_ам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0<m_ам<1 (рисунок 4б). При m_ам>1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).

Основными достоинствами амплитудной модуляции являются:

· узкая ширина спектра АМ сигнала;

· простота получения модулированных сигналов.

Недостатками этой модуляции являются:

· низкая помехоустойчивость (т. к. при воздействии помехи на сигнал искажается его форма — огибающая, которая и содержит передаваемое сообщение);

· неэффективное использование мощности передатчика (т. к. наибольшая часть энергии модулированного сигнала содержится в составляющей несущего сигнала до 64%, а на информационные боковые полосы приходится по 18%).

Амплитудная модуляция нашла широкое применение:

· в системах телевизионного вещания (для передачи телевизионных сигналов);

· в системах звукового радиовещания и радиосвязи на длинных и средних волнах;

· в системе трехпрограммного проводного вещания.

Дата добавления: 2014-01-03