Частотная модуляция

Частотная модуляция - процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

u(t) = Um_u sin? t

на несущее колебание

S(t) = Um sin(?₀t+?)

происходит изменение частоты несущего сигнала по закону:

w_чм(t) =?₀+а_чм Um_u sin? t (9)

где а_чм — коэффициент пропорциональности частотной модуляции.

Поскольку значение sin? t может изменятся в диапазоне от -1 до 1, то наибольшее отклонение частоты ЧМ сигнала от частоты несущего сигнала составляет

??_m= а_чм Um_u (10)

Величина Dw_m называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.

Значение? _чм(t) непосредственно подставить в S(t) нельзя, т. к. аргумент синуса? t+j является мгновенной фазой сигнала?(t) которая связана с частотой выражением

?=d?(t)/dt (11)

Отсюда следует что, чтобы определить?_чм(t) необходимо проинтегрировать? _чм(t)

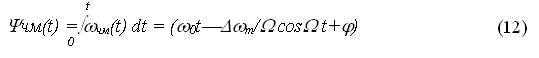
Причем в выражении (12)? является начальной фазой несущего сигнала.

Отношение

Мчм =? ?_m/? (13)

называется индексом частотной модуляции.

Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Sчм(t)=Um sin(?₀t — Мчм cos? t+?) (14)

Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.

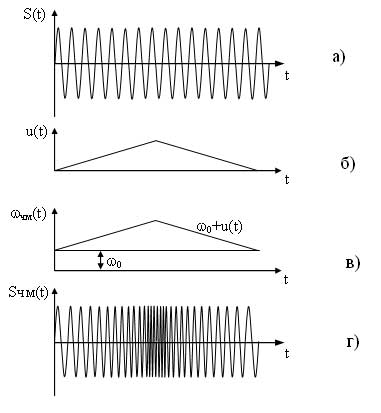
Рисунок 7 - Формирование ЧМ сигнала

Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим

Sчм(t)= Um J₀(Mчм) sin(?₀t+?) -

-Um J₁(Mчм) {cos[(?₀ -?)t+j]+ cos[(?₀+?)t+?]} -

- Um J₂(Mчм) {sin[(?₀ - 2?)t+j]+ sin[(?₀+2?)t+?]}+

+ Um J₃(Mчм) {cos[(?_{0 -} 3?)t+j]+ cos[(?₀+3?)t+?]} -

- Um J₄(Mчм) {sin[(?₀ - 4?)t+j]+ sin[(?₀+4?)t+?]} -… (15)

где J_k(Mчм) — коэффициенты пропорциональности.

J_k(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как

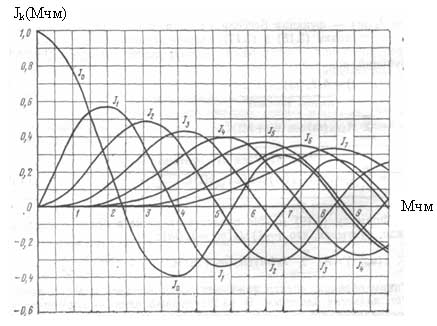
Рисунок 8 - Функции Бесселя

видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличением индекса увеличивается и количество составляющих спектра). Например, необходимо определить коэффициенты J_k(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J₀, J₁, J₂, J₃, J₄) Их значение при заданном индексе будет равно: J₀=0,21; J₁=0,58; J₂=0,36; J₃=0,12; J₄=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J₀) и по четыре составляющих в каждой боковой полосе (Um J₁; Um J₂; Um J₃; Um J₄).

Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J₀(Мчм) будет равно нулю (в месте пересечения функции J₀ с осью Мчм), например Мчм=2,4.

Поскольку увеличение составляющих приводит к увеличению ширины спектра ЧМ сигнала, то значит, ширина спектра зависит от Мчм (рисунок 9). Как видно из рисунка, при Мчм?0,5 ширина спектра ЧМ сигнала соответствует ширине спектра АМ сигнала и в этом случае частотная модуляция является узкополосной, при увеличении Мчм ширина спектра увеличивается, и модуляция в этом случае является широкополосной. Для ЧМ сигнала ширина спектра определяется

D?_чм=2(1+Мчм)? (16)

Достоинством частотной модуляции являются:

· высокая помехоустойчивость;

· более эффективное использование мощности передатчика;

· сравнительная простота получения модулированных сигналов.

Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.

Частотная модуляция используется:

· в системах телевизионного вещания (для передачи сигналов звукового сопровождения);

· системах спутникового теле- и радиовещания;

· системах высококачественного стереофонического вещания (FM диапазон);

· радиорелейных линиях (РРЛ);

· сотовой телефонной связи.

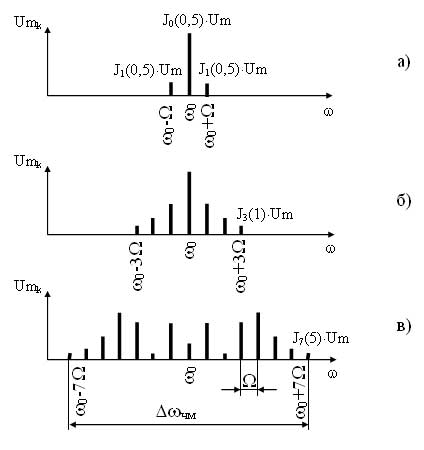
Рисунок 9 - Спектры ЧМ сигнала при гармоническом модулирующем сигнале и при различных индексах Мчм: а) при Мчм=0,5, б) при Мчм=1, в) при Мчм=5

Дата добавления: 2014-01-03