Фазовая модуляция

Фазовая модуляция - процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

u(t) = Um_u sin? t

на несущее колебание

S(t) = Um sin(?₀t+?)

происходит изменение мгновенной фазы несущего сигнала по закону:

?фм(t) =?₀t+?+а_фм Um_u sin? t (17)

где а_фм — коэффициент пропорциональности частотной модуляции.

Подставляя? фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:

Sфм(t) = Um sin(?₀t+а_фм Um_u sin? t+?) (18)

Произведение а_фм Um_u=Dj_m называется индексом фазовой модуляции или девиацией фазы.

Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:

?_фм(t)=d?фм(t)/dt=w₀+а_фмUm_u? cos? t (19)

Произведение а_фмUm_u? =?? _m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.

Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.

При разложении математической модели ФМ сигнала на гармонические составляющие получится такой же ряд, как и при частотной модуляции (15), с той лишь разницей, что коэффициенты J_k будут зависеть от индекса фазовой модуляции?? _m (J_k(?? _m)). Определятся эти коэффициенты будут аналогично, как и при ЧМ, т. е. по функциям Бесселя, с той лишь разницей, что по оси абсцисс необходимо заменить Мчм на?? _m. Поскольку спектр ФМ сигнала строится аналогично спектру ЧМ сигнала, то для него характерны те же выводы что и для ЧМ сигнала (пункт 1.4).

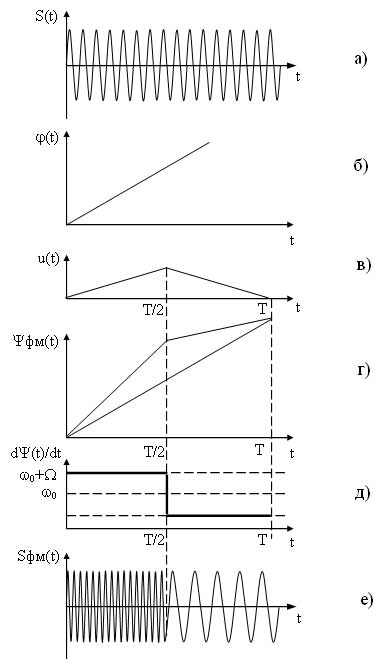
Рисунок 10 - Формирование ФМ сигнала

Ширина спектра ФМ сигнала определяется выражением:

??_фм=2(1+?j_m)? (20).

Достоинствами фазовой модуляции являются:

· высокая помехоустойчивость;

· более эффективное использование мощности передатчика.

· недостатками фазовой модуляции являются:

· большая ширина спектра;

· сравнительная трудность получения модулированных сигналов и их детектирование

Дискретная двоичная модуляция (манипуляция гармонической несущей)

Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.

Различают четыре вида манипуляции:

· амплитудную манипуляцию (АМн или АМТ);

· частотную манипуляцию (ЧМн или ЧМТ);

· фазовую манипуляцию (ФМн или ФМТ);

· относительно-фазовую манипуляцию (ОФМн или ОФМ).

Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.

При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая S_АМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).

При частотной манипуляции используются две частоты?₁ и?₂. При наличии импульса в модулирующем сигнале (посылке) используется более высокая частота?₂, при отсутствии импульса (активной паузе) используется более низкая частота w₁ соответствующая немодулированной несущей (рисунок 11, г)). Спектр частотно-манипулированного сигнала S_ЧМн(t) имеет две полосы возле частот?₁ и?₂.

При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).

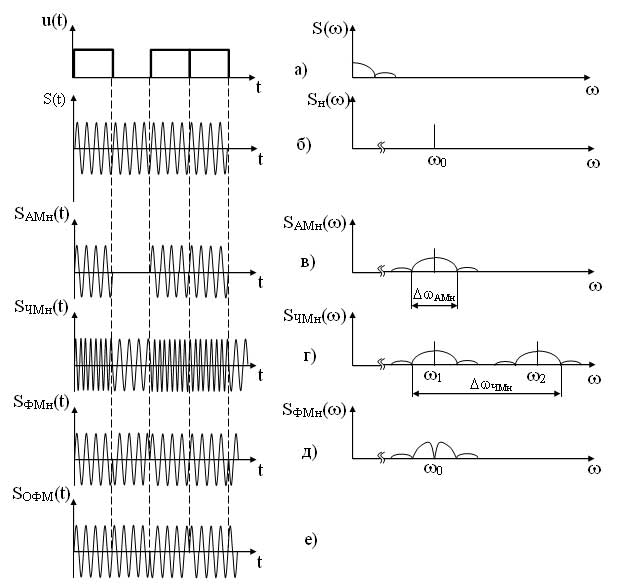
Рисунок 11 - Временные и спектральные диаграммы модулированных сигналов различных видов дискретной двоичной модуляции

При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).

Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.

В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).

Дата добавления: 2014-01-03