Метод Галеркина

Пусть имеем линейную краевую задачу. Обозначим

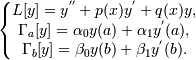
Пусть на отрезке [ a, b ] задана система базисных функций u ₀(x), u ₁(x),..., u_n (x),..., удовлетворяющая следующим условиям.

1) Система u ₀(x), u ₁(x),..., u_n (x),..., является ортогональной, то есть

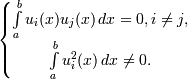
2) Система является полной, то есть не существует никакой другой отличной от нуля функции, ортогональной ко всем функциям u_i (x)(i = 0,1,2,....

3) Конечная система базисных функций 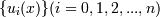выбирается так,чтобы функция u ₀(x) удовлетворяла неоднородным краевым условиям Γ _a [ u ₀] = A,Γ _b [ u ₀] = B,а функции u_i (x)(i = 0,1,2,..., n) удовлетворяли бы однородным краевым условиям Γ _a [ u_i ] = Γ _b [ u_i ] = 0,(i = 0,1,2,..., n).Решение краевой задачи будем искать в виде 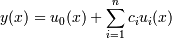. Из условий следует, что эта функция удовлетворяет краевым условиям.

Рассмотрим выражение, называемое невязкой: 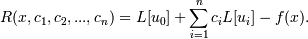Выберем коэффициенты c_i таким образом, чтобы значение интеграла от квадрата невязки 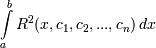было наименьшим. Доказано, что это достигается лишь в том случае, если невязка R (x, c ₁, c ₂,..., c_n) ортогональна ко все базисным функциям u_i.

Записываем уравнение ортогональности: 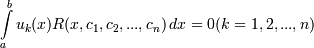или в более подробной записи 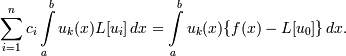Мы получили систему линейных алгебраических уравнений относительно коэффициентов c_i.

Заметим, что при выборе базисных функций условие ортогональности не является обязательным, если подобрать коэффициенты из условия минимальности интеграла. Так, например, взяв за основу полную систему функций, ортогональных на отрезке [ a, b ], можно выбрать в качестве базисных функций линейные комбинации функций из этой системы. Достаточно лишь, чтобы выбранные функции были линейно независимы на отрезке [ a, b ].

Дата добавления: 2014-01-03