Примеры реализации численных методов решения систем дифференциальных уравнений

Примеры решений

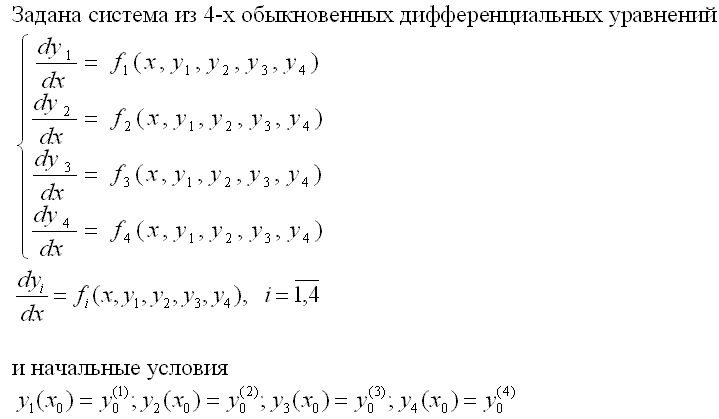
Рассмотрим некоторые численные методы решения заданной системы.

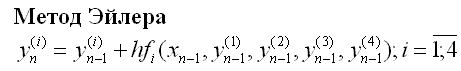
Программная реализация (Turbo Pascal)

program Euler;var T: Text; a, b, h, x: real; y1, y2, y3, y4, y1_1, y1_2, y1_3, y1_4: real; function F(x, y1, y2, y3, y4: real; n:byte):real;begin case n of 1: f:=-y2; 2: f:=y1; 3: f:=y1-y4; 4: f:=y2+y3; end;end;begin assign(T, 'c:\euler.txt'); rewrite(T); a:=0; b:=2*pi; h:=pi/40; y1:=1; y2:=0; y3:=0; y4:=0; x:=a; while x<=b+h do begin writeln(T, x:10:5, y1:10:5, y2:10:5, y3:10:5, y4:10:5); y1_1:=y1+h*f(x, y1, y2, y3, y4, 1); y1_2:=y2+h*f(x, y1, y2, y3, y4, 2); y1_3:=y3+h*f(x, y1, y2, y3, y4, 3); y1_4:=y4+h*f(x, y1, y2, y3, y4, 4); y1:=y1_1; y2:=y1_2; y3:=y1_3; y4:=y1_4; x:=x+h; end; flush(T); close(T);end.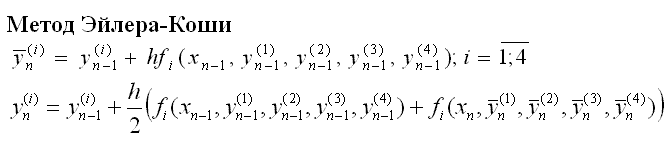

Программная реализация (Turbo Pascal)

program Euler_Koshi;var T:Text; x,h,a,b,y1, y2, y3, y4, y1_1, y1_2, y1_3,y1_4, y11, y12, y13, y14:real;function F(x, y1, y2, y3, y4: real; n:byte):real;begin case n of 1: f:=-y2; 2: f:=y1; 3: f:=y1-y4; 4: f:=y2+y3; end;end;begin assign(T, 'd:\euler_k.txt'); rewrite(T); a:=0; b:=2*pi; h:=pi/160; y1:=1; y2:=0; y3:=0; y4:=0; x:=a; while x<=b+h do begin writeln(T, x:10:5, y1:10:5, y2:10:5, y3:10:5, y4:10:5, cos(x):10:5, sin(x):10:5, x*cos(x):10:5, x*sin(x):10:5); y1_1:=y1+h*f(x, y1, y2, y3, y4, 1); y1_2:=y2+h*f(x, y1, y2, y3, y4, 2); y1_3:=y3+h*f(x, y1, y2, y3, y4, 3); y1_4:=y4+h*f(x, y1, y2, y3, y4, 4); y11:=y1+h/2*(f(x, y1, y2, y3, y4, 1)+f(x+h,y1_1, y1_2, y1_3, y1_4, 1)); y12:=y2+h/2*(f(x, y1, y2, y3, y4, 2)+f(x+h,y1_1, y1_2, y1_3, y1_4, 2)); y13:=y3+h/2*(f(x, y1, y2, y3, y4, 3)+f(x+h,y1_1, y1_2, y1_3, y1_4, 3)); y14:=y4+h/2*(f(x, y1, y2, y3, y4, 4)+f(x+h,y1_1, y1_2, y1_3, y1_4, 4)); y1:=y11; y2:=y12; y3:=y13; y4:=y14; x:=x+h; end; flush(T); close(T);end.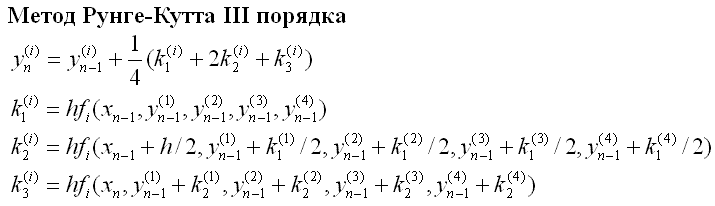

Программная реализация (Turbo Pascal)

program rk_III;var T:Text; x,h,a,b,y1, y2, y3, y4, k1_1, k1_2, k1_3, k1_4, k2_1, k2_2, k2_3, k2_4, k3_1, k3_2, k3_3, k3_4:real;function F(x, y1, y2, y3, y4: real; n:byte):real;begin case n of 1: f:=-y2; 2: f:=y1; 3: f:=y1-y4; 4: f:=y2+y3; end;end;begin assign(T, 'd:\rk_iii.txt'); rewrite(T); a:=0; b:=2*pi; h:=pi/160; y1:=1; y2:=0; y3:=0; y4:=0; x:=a; while x<=b+h do begin writeln(T, x:10:5, y1:10:5, y2:10:5, y3:10:5, y4:10:5, cos(x):10:5, sin(x):10:5, x*cos(x):10:5, x*sin(x):10:5); k1_1:=h*f(x, y1, y2, y3, y4, 1); k1_2:=h*f(x, y1, y2, y3, y4, 2); k1_3:=h*f(x, y1, y2, y3, y4, 3); k1_4:=h*f(x, y1, y2, y3, y4, 4); k2_1:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 1); k2_2:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 2); k2_3:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 3); k2_4:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 4); k3_1:=h*f(x+h,y1+k2_1, y2+k2_2, y3+k2_3, y4+k2_4, 1); k3_2:=h*f(x+h,y1+k2_1, y2+k2_2, y3+k2_3, y4+k2_4, 2); k3_3:=h*f(x+h,y1+k2_1, y2+k2_2, y3+k2_3, y4+k2_4, 3); k3_4:=h*f(x+h,y1+k2_1, y2+k2_2, y3+k2_3, y4+k2_4, 4); y1:=y1+1/4*(k1_1+2*k2_1+k3_1); y2:=y2+1/4*(k1_2+2*k2_2+k3_2); y3:=y3+1/4*(k1_3+2*k2_3+k3_3); y4:=y4+1/4*(k1_4+2*k2_4+k3_4); x:=x+h; end; flush(T); close(T);end.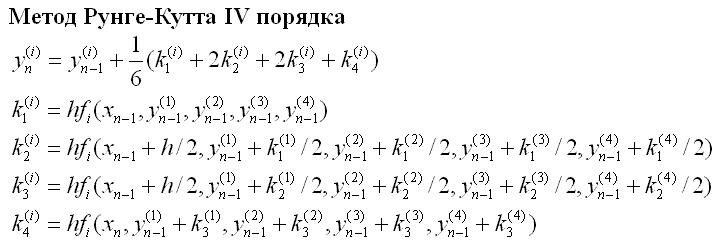

Программная реализация (Turbo Pascal)

program rk_iv;var T:Text; x,h,a,b,y1, y2, y3, y4, k1_1, k1_2, k1_3, k1_4, k2_1, k2_2, k2_3, k2_4, k3_1, k3_2, k3_3, k3_4, k4_1, k4_2, k4_3, k4_4:real;function F(x, y1, y2, y3, y4: real; n:byte):real;begin case n of 1: f:=-y2; 2: f:=y1; 3: f:=y1-y4; 4: f:=y2+y3; end;end;begin assign(T, 'd:\rk_iv.txt'); rewrite(T); a:=0; b:=2*pi; h:=pi/80; y1:=1; y2:=0; y3:=0; y4:=0; x:=a; while x<=b+h do begin writeln(T, x:10:5, y1:10:5, y2:10:5, y3:10:5, y4:10:5, cos(x):10:5, sin(x):10:5, x*cos(x):10:5, x*sin(x):10:5); k1_1:=h*f(x, y1, y2, y3, y4, 1); k1_2:=h*f(x, y1, y2, y3, y4, 2); k1_3:=h*f(x, y1, y2, y3, y4, 3); k1_4:=h*f(x, y1, y2, y3, y4, 4); k2_1:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 1); k2_2:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 2); k2_3:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 3); k2_4:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 4); k3_1:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 1); k3_2:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 2); k3_3:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 3); k3_4:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 4); k4_1:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 1); k4_2:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 2); k4_3:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 3); k4_4:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 4); y1:=y1+1/6*(k1_1+2*k2_1+2*k3_1+k4_1); y2:=y2+1/6*(k1_2+2*k2_2+2*k3_2+k4_2); y3:=y3+1/6*(k1_3+2*k2_3+2*k3_3+k4_3); y4:=y4+1/6*(k1_4+2*k2_4+2*k3_4+k4_4); x:=x+h; end; flush(T); close(T);end.

ЛИТЕРАТУРА

1. Демидович Б. П., Моденов В. П. Дифференциальные уравнения: Учебное пособие. 3-е изд., стер. — СПб.: Издательство «Лань», 2008. — 288 с: ил. — (Учебники для вузов. Специальная литература). ISBN 978-5-8114-0677-7.

2. Виленкин Н. Я. и др. Дифференциальные уравнения: Учеб. пособие для студентов-заочников IV курса физ.-мат, фак. / Н. Я. Виленкин, М. А. Доброхотова, А. Н. Сафонов.— М.: Просвещение, 1984. — 176 с. — Моск. гос. заоч. пед. ин-т.

3. Матвеев Н. М. Дифференциальные уравнения. Учеб. пособие для студентов пед. ин-тов по физ.-мат. спец.— М.: Просвещение, 1988.— 256. - ISBN 5-09-000281-9

4. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. - 4 изд. - М., Наука, 1974. - 331 с.

5. Ф. Трикоми. Дифференциальные уравнения. 1962 год. 362 стр.

6. Филиппов Алексей Федорович Введение в теорию дифференциальных уравнений: Учебник. Изд. 2-е, испр. М.: КомКнига, 2007. - 240 с.

7. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. - 424 с.

8. Васильева А. Б., Медведев Г. Н., Тихонов Н. А., Уразгильдина Т. А. Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и задачах. — 2-е изд., испр. — М.: ФИЗМАТЛИТ, 2005. — 432 с. — (Курс высшей математики и математической физики. Вып. 10) - ISBN 5-9221-0628-7.

9. Калинин В.В. Обыкновенные дифференциальные уравнения (пособие для практических занятий). – ФГУП Изд-во «Нефть и газ»
РГУ нефти и газа им. И.М. Губкина, 2005. – 68 с.

10. Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах. - М.: Изд-во МАИ, 2000.- 380с: ил.

11. Ибрагимов Н.Х. Практический курс дифференциальных уравнений и математического моделирования. Классические и новые методы. Нелинейные математические модели. Симметрия и принципы инвариантности / Перевод с англ. И. С. Емельяновой. - Нижний Новгород: Издательство Нижегородского госуниверситета, 2007. 421с. ISBN 91-7295-988-6 (Alga Publications, Blekingc Institute of Technology) ISBN 978-5-91326-027-7

12. Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. - М.: ФИЗМАТЛИТ, 2001. — 576 с.

13. Зайцев В.Ф., Полянин А.Д. Справочник по дифференциальным уравнениям с частными производными первого порядка. М.: ФИЗМАТЛИТ, 2003. — 416 с.

14. Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. Пер. с нем. - 4-е изд., испр. — М.: Наука: Гл. ред. физ-мат. лит., 1971. — 576с.

15. Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики: Учеб. для вузов. 2-е изд. / Под ред. B.C. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. - 368 с. (Сер. Математика в техническом университете; Вып. XII).

16. Власова Е.А., Зарубин B.C., Кувыркин Г.Н. Приближенные методы математической физики: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. -700 с. (Сер. Математика в техническом университете; Вып. XIII).

Дата добавления: 2014-01-03