Моделирование мышечного сокращения

Уравнение Хилла 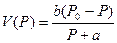было получено при обобщении большого количества данных. Вид этого уравнения указывает на существование в мышце внутреннего вязкого (зависящего от скорости) трения, препятствующего ее укорочению. Однако природа этого, как и физический смысл констант а и оставались не ясными.

ми. Объяснения этих и ряда других явлений были даны в математической модели сокращения мышцы, предложенной В. Дещеревским, на модели скользящих нитей.

Предполагается, что сила сокращения волокна равна сумме сил, генерируемых мостиками в слое, равном половине саркомера, т.к. саркомеры по толщине волокна включены параллельно. Скорость изменения длины волокна V_в: V_в = 2NV, где N - число саркомеров в волокне, V – относительная скоростъ скольжения нитей. При скольжении нитей мостик

может находиться в одном из трёх возможных состояний: разомкнутое, замкнутое тянущее, когда головка генерирует силу, направленную к центру саркомера, и замкнутое тормозящее, когда актиновая нить прошла координату центра прикрепле­ния головки и прикрепленный мостик создает отрицательную по направлению силу F, поcле чего он размыкается.

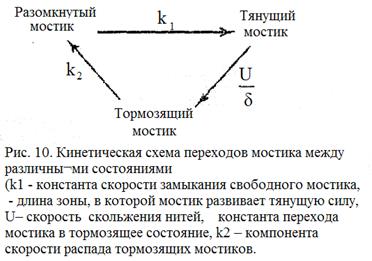Переходы из одного состояния в другое, представленные на рис10, определяются соответствующими константами ско­ростей. Полный цикл мостика сопровождается распадом моле­кул АТФ. Для общего числа тянущих (х) и тормозящих (z) мостиков развиваемая саркамером сила F:

Очевидно, что первое слагаемое—это сила, генерируемая зам­кнутыми, а второе - тормозящими мостиками. Тогда система кинетических дифференциальных уравнений для состояний мостиков может быть записана в виде:

где - число мостиков, способных замыкаться при длине 0,5 саркомера в слое волокна толщиной l. М- масса нагрузки, Р - сила, развиваемая волокном.

Смысл кинетических уравнений достаточно ясен.

Например, в первом уравнении левая часть - скорость изменения количества тянущих мостиков. В правой части первое сла­гаемое - общее число мостиков, минус количество тянущих х и тормозящих z мостиков, т.е. в квадратных скобках - количество оставшихся разомкнутых мостиков. Умножая это количество на константу , получаем скорость увеличения количества тянущих мостиков (верхняя стрелка на рис 10); второе слагаемое - скорость уменьшения количества тянущих мостиков за счет их перехода в тормозное состояние (правая стрелка рис.10). Разность между скоростями роста и убыва­ния количества тянущих мостиков дает искомую скорость из­менения их количества. Уравнения 2 и 3записыва­ются аналогично

При изотоническом сокращении с постоянной скоростью в области с постоянным числом мостиков (состояние б на рис. 3) - максимальному числу мостиков, которые могут участвовать в сокращении.

В этом случае ззначения величин x, z и U не меняются во времени, т.е. система находится в стационарном состоянии:

Тогда из системы уравнений и условия стационарности получаем:

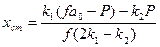
Выражение для стационарной скорости укорочения совпадает с уравнением Хилла.

При этом:

Т. е., если эти выражения подставить в последнее уравнение (для скорости ), то получается уравнение Хилла.

Таким образом, кинетическая модель В. Дещеревского позволи­ла объяснить феноменологическое уравнение Хилла, смысл констант а и b, входящих в него, смысл величины максимальной силы изометрического сокращения. Кроме того, показано, что внутренняя вязкая компонента мышцы определяется силой развиваемой тормозящими мостиками, число которых растет с увеличением скорости сокращения мышцы.

Исходя из данных электронной микроскопии, рентгеноструктурного анализа и предложенной модели, было рассчи­тано, что на одну нить актина приходится усилие при максимальной изометрической нагрузке Считая, что в каждой структурной единице находится 1 молекула миозина и за каждый цикл замыкание –размыкание расщепляется 1 молекула АТФ, энергия которой использует­ся на 50 %, подучены следующие характеристики единично­го элемента: энергия сокра­щения , 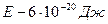время замыкания 1 мс. Таким образом сила, генерируемая единичным элементом, лишь в 3 раза пре­вышает силу тяготения двух масс 1 г на расстоянии 1 мм. равную . Целая же мышца может развивать силу до 1 тонны, то есть на 16 порядков больше.

Дата добавления: 2017-01-14