Приклади розв’язування задач. Задача 1Вважаючи сонячне випромінювання близьким до випромінювання абсолютно чорного тіла, оцінити температуру поверхні Сонця

Задача 1 Вважаючи сонячне випромінювання близьким до випромінювання абсолютно чорного тіла, оцінити температуру поверхні Сонця, враховуючи, що густина енергетичної світимості сягає максимуму при довжині хвилі λ_max = 500 нм.

Розрахувати величину сонячної сталої для Землі.

Розв’язок

Знайдемо температуру Сонця. Згідно першому закону Віна:

λ_max Т = С₁, тобто .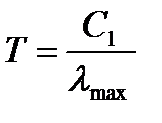

Вважаючи, що випромінювання Сонця близьке до випромінювання абсолютно чорного тіла, знайдемо енергію Q, яку випромінює Сонце за проміжок часу Δ t. За визначенням енергетичної світимості,та згідно закону Стефана-Больцмана маємо:

; ,

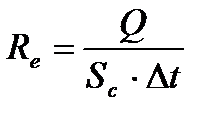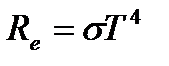де 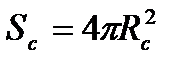– площа Сонця, а R_с – радіус Сонця. Таким чином енер­гія, що випромінює Сонце за час Δ t дорівнює:

.

Ця енергія рівномірно розподіляється по поверхні сфери площею:

де R – відстань від Землі до Сонця.

За визначенням сонячної сталої це є кількість променевої енергії, що випромінює Сонце за одиницю часу через одиницю площі перпендикулярно до сонячних променів, яка розташована на такій самій відстані від Сонця, що і Земля. Таким чином для сонячної сталої маємо:

Після розрахунків одержуємо:

, .

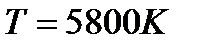Задача 2 Визначити, в скільки разів буде ослаблений промінь природного світла, якщо пропустити його через два ніколі, площини поляризації яких становлять кут φ = 45°. Вважати, що при про­ходженні через кожний ніколь інтенсивність світла внаслідок відбивання і поглинання зменшується на 10%.

Розв'язок.Для розв’язання задачі потрібно застосувати закон Малюса, який встановлює залежність інтенсивності поляризованого променя I, що пройшов через аналізатор, від кута між площинами поляризації поляризатора та аналізатора і від інтенсивності I ₀ променя, що падає на аналізатор:

I = I ₀cos² j.

В задачі потрібно знайти відношення інтенсивностей природного променя і променя, що пройшов крізь аналізатор, тобто I _пр/ I.

Якщо природний промінь пройде крізь поляризатор, то інтен­сивність його зменшиться, по-перше, в 2 рази тому що з призми вий­де тільки незвичайний промінь I ₀ (звичайний зазнає повне внутрішнє відбивання) і, по-друге, інтенсивність I ₀ незвичайного променя змен­шиться ще на 10%; при проходженні крізь поляризатор, внаслідок відбивання і поглинання.

Отже,

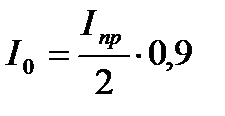
Потім інтенсивність I променя, що пройшов ще раз крізь аналізатор, виявиться менша від інтенсивності I ₀ не тільки у відповідності з законом , але і від втрат при відбиванні та поглинанні аналізатором (10%).

Тому формула Малюса з врахуванням інтенсивності світла в гаслі доки поглинання аналізатором набуде вигляду:

I = I ₀cos² j ×0,9,

але тому що , то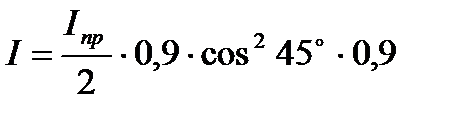

Знаходимо відношення:

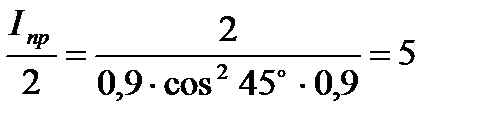
Отже, природний промінь світла при пропусканні його крізь два ніколі, відповідно до умов задачі, буде ослаблений в 5 разів.

Задача 3 Відстань між двома п'ятидесятисвічковими лампа­ми, що прикріплені до стелі l = 4 м. Обчислити освітлюваність стола в люксах, якщо він перебуває під однією з ламп і посередині між лампами. Відстань від поверхні стола до стелі h = 2м.

Розв'язок. Знаходимо суму освітлюваностей від двох ламп, маючи на увазі, що св. Освітлюваність у першому (рис. 1) випадку дорівнює:

де

Рисунок 1. Рисунок 2.

Отже,

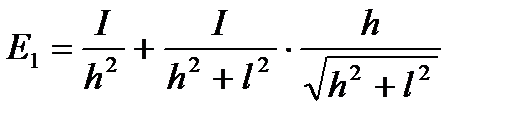
Освітлюваність у другому випадку (рис. 2) дорівнює

,

де

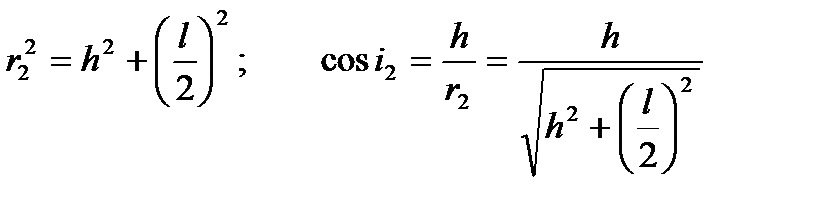
Отже,

Задачу розв'язуємо в системі СІ. Підставляючи числові значення величин у вирази для Е ₁ та Е ₂ знайдемо:

ЗАВДАННЯ: законспектувати матеріал, розглянути розв’язки задач, виконати презентації (реферати) на теми:

1 Сонячні батареї. Люксметр.

2 Фотометри.

3 Екстракційно-фотометричний метод визначення важких металів у природних водах.

4 Фотометричні технології.

ФОРМА КОНТРОЛЮ: перевірка конспекту самостійної роботи, виконання завдань.

ВИКЛАДАЧ – Марінець І.С.

САМОСТІЙНА РОБОТА № 13 (2 год.)

ТЕМА: Геометрична оптика

МЕТА: Познайомити студентів з геометричною оптикою, як граничним випадком хвильової оптики; показати па практиці застосування її методів у розрахунках при конструюванні різних оптичних приладів. Формувати спостережливість та вміння аналізувати і робити висновки, розвивати теоретичне і логічне мислення та вміння самостійно здобувати знання.

ПЕРЕЛІК ПОСИЛАНЬ:

1 Бушок Г.Ф.Курс фізики. Кн.2. / Г.Ф. Бушок, Є.Ф. Венгер. – К.: Вища школа, 2002, с.

2 Кучерук І.М. Загальний курс фізики. У трьох томах. Т. 2. / І.М.Кучерук, І.Т Горбачук, П.П. Луцик. – К.: Техніка, 2006, с.

Дата добавления: 2017-01-14