Геометрична оптика – граничний випадок хвильової оптики

ПЛАН

1 Геометрична оптика – граничний випадок хвильової оптики.

2 Плоскопаралельна пластина. Кільця Ньютона.

3 Оптичні прилади.

ЗМІСТ ТЕОРЕТИЧНОГО МАТЕРІАЛУ:

Принцип Гюйгенса та його застосування до закону заломлення світла. Повне внутрішнє відбивання.

Принцип Гюйгенса стверджує, що кожна точка хвильової поверхні являється джерелом вторинних хвиль. Цей принцип дає можливість по відомому в момент часу t положенню фронту хвилі знайти його положення в наступний момент часу t + Δt.

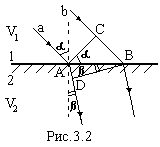Розглянемо в рамках цього принципу закон заломлення світла. На межу двох оптичних середовищ 1 і 2 падає плоска хвиля під кутом падіння α (рис.2). В момент часу, коли промінь а досягає межі поділу (точка А) і переходить у друге середовище, промінь b досягає точки С. За час Δt промінь b пройде відстань ВС із швидкістю V₁, а промінь а – відстань AD із швидкістю V₂ під кутом заломлення β. Відрізки ВС і АD виражаємо через загальну гіпотенуза АВ у відповідні кути

.

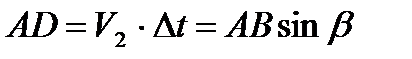Поділимо рівняння одне на одне. Одержуємо закон заломлення: відношення синуса кута падіння до синуса кута заломлення постійне для двох середовищ, дорівнює відношенню швидкостей світла і називається відносним показником заломлення другого середовища відносно першого

.

Показник заломлення середовища відносно вакууму називається абсолютним показником заломлення цього середовища

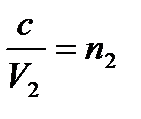, . Відношення дає можливість по абсолютним показникам, які можна знайти в довіднику, розрахувати відносний показник заломлення будь-якої пари оптичних середовищ.

Абсолютний показник заломлення показує у скільки разів швидкість світла, або довжина хвилі λ в середовищі менша, ніж λ_о у вакуумі. Чим більший абсолютний показник заломлення, тим оптична густина середовища більша. Враховуючи це, маємо .

При переході променя в середовище з більшою оптичною густиною β > α. Заломлений промінь віддаляється від перпендикуляра до межі середовищ (рис.3). Коли кут заломлення β стає прямим, кут падіння називається граничним кутом α_гр. При кутах α > α_гр промінь у друге середовище не переходить, а повністю відбивається. Це явище називається явищем повного внутрішнього відбивання. Так як , Граничний кут знаходиться із умови

Явище повного внутрішнього відбивання покладене в основу роботи поворотних (рис.4,а), оборотних (рис.4,б) призм і світловодів (рис.4,с). Поворотна призма відхиляє промінь на певний кут, оборотна перевертає зображення, тобто повертає промінь вздовж напрямку його поширення, світловод провидить промінь по своїй внутрішній частині, показник заломлення якої більший, ніж оболонки. Реальний світловод складається з величезної кількості тонких структур, зображених на рис.4,с, тому його можна згинати як звичайний електричний кабель.

Плоскопаралельна пластина. Кільця Ньютона.

Розглянемо в пучку світла, що падає на поверхню плоско-паралельної пластинки два промені 1 і 2 (рис.5). Кожний із них частково відбивається і частково, заломлюючись, переходить всередину пластинки. Теж саме відбувається і на тильній поверхні. Розглянемо такі два промені: у промені 1 той, який заломившись у точці А, перейшов у пластинку, на тильній стороні у точці D відбився і знову заломившись вийшов із пластинки у точці С; у промені 2 той, що в точці С відбився від лицевої поверхні. Ці промені 1^' і 2^' накладаються, тобто виникає інтерференція, результат якої залежить від оптичної різниці ходу Δ. Знайдемо її. Фронт падаючого променя це площина АВ. Промінь 1 проходить шлях AD+DC в середовищі з показником заломлення n. Його оптичний шлях дорівнює (AD+DC)∙n. За цей же час промінь 2 проходе відстань ВС. Тому оптична різниця ходу Δ=(AD+DC)∙n-ВС.

Виражаємо ці відрізки через товщину пластинки b та кути: падіння α і заломлення β. ,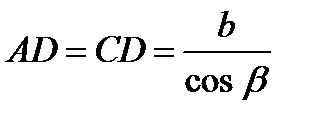

. Одержимо .

Звільняємось від кута β скориставшись законом заломлення та основною тригонометричною тотожністю

.

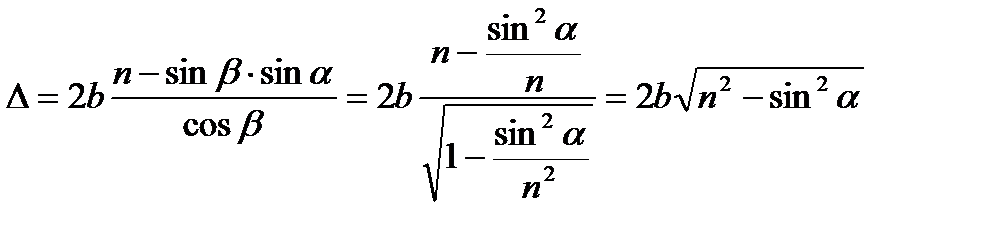При відбиванні світла від оптично густішого середовища (точка С) фаза хвилі змінюється на протилежну. Враховуючи це оптична різниця ходу буде на половину довжини хвилі меншою, тобто .

Одержимо, що максимум інтерференційної картини у відбитих променях буде мати місце при умові ,

а мінімум при умові .

При падінні променя на клин (рис. 6) інтерференційні смуги (максимуми чи мінімуми) спостерігаються в тих місцях, де товщина клина однакова і задовольняє відповідній умові для максимуму і для мінімуму. Тому такі лінії називаються лініями однакової товщини. Запишемо умову максимуму для двох сусідніх ліній: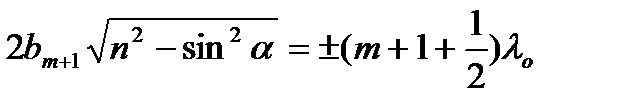

.

Віднімемо друге рівняння із першого .

Із прямокутного трикутника маємо .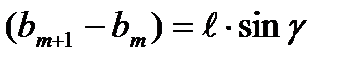

Отже . При малих кутах γ клина . Як правило кут падінні променів близький до 0^о, тобто промені падають на поверхню клина перпендикулярно. При таких умовах одержуємо . Цей вираз дає можливість застосувати явище інтерференції для вимірювання надзвичайно малих кутів клина по відомим довжині хвилі λ_о і показнику заломлення n та експериментально виміряній відстані ℓ між інтерференційними лініями.

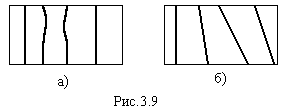
Крім цього по виду ліній однакової товщини і їх паралельності можна візуально виявити дефекти полірування клина (рис. 7): а) на поверхні клина є нерівності; б) кут клина неоднаковий.

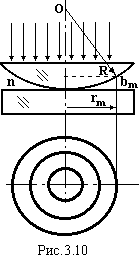Різновидністю інтерференції на клині і ліній однакової товщини є так звані кільця Ньютона. У цьому випадку клин утворюється між сферичною поверхнею і площиною (рис. 8). Промені, як правило, падають перпендикулярно (кут падіння α = 0^о) до плоскої поверхні. Інтерференційні лінії однакової товщини мають вид концентричних кілець. Їх можна спостерігати як у відбитих променях, так і у променях, які пройшли через оптичну систему. Знайдемо радіуси r_m кілець. По теоремі Піфагора маємо

, або .

Щоб кільця не зливались одне з одним, радіус кривизни R сферичної поверхні беруть досить великим. Це дає право знехтувати доданком як величиною, набагато меншою порівняно з іншими. Одержуємо . Скориставшись, що α = 0^о, одержимо радіуси світлих і темних кілець

, .

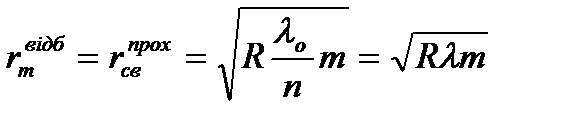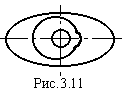Рівність радіусів зумовлена тим, що у випадку спостереження у відбитих променях має місце втрата половини довжини хвилі, а в прохідних променях такої втрати немає.

Якщо сферична, чи плоска поверхня, які утворюють клин, мають дефекти, то їх можна візуально виявити по неправильній формі кілець, або їх не концентричності (рис. 9). Для однозначності трактування цих відхилень необхідно мати одну із поверхонь еталонну.

Дата добавления: 2017-01-14