Рівняння площини у відрізках

Приклад

Вектором. Загальне рівняння площини

Рівняння площини за точкою і нормальним

Площина

При побудові площини в просторі будемо використовувати аналогії для прямої лінії на площині. Як і для прямої лінії можемо стверджувати, що між множиною всіх площин простору і множиною лінійних рівнянь відносно трьох змінних існує взаємно однозначна відповідність.

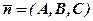Нехай в просторі задана точка і ненульовий вектор . Через точку можна провести єдину

Рис.11

площину 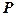перпендикулярно вектору . Щоб отримати рівняння

площини, виберемо на ній довільну точку і розглянемо

вектор (див. рис. 11).

Точка тоді і тільки тоді, коли

— рівняння площини що проходить через дану точку з нормальним вектором.

Розкривши дужки в (17) маємо

— загальне рівняння площини, де позначено .

Отже, площині 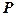відповідає лінійне рівняння (18). Навпаки, якщо задано лінійне рівняння вигляду (18), то неважко знайти точку , координати якої задовольняють це рівняння, і записати вектор 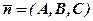. Вектор 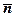і точка визначають єдину площину .

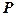Дано точки М(-4,6,-6) і N(-9,2,-5). Скласти рівняння площини, яка проходить через точку М і перпендикулярна до вектора .

Розв’язання. За умовою вектор є нормальним вектором площини. Знайдемо його координати

Підставляючи в рівняння (17) А=-5, В=-4, С=1, а також х₁=-4, у₁=6, z=-6, маємо .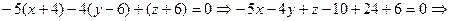

Якщо в загальному рівнянні

жодне з чисел не дорівнює нулю, то площину можна побудувати за трьома точками перетину її з координатними осями:

, де відрізки, які відтинає площина на координатних осях (див. рис. 12).

Рис.12

Рівняння площини у відрізках запишеться:

Прямі 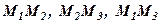називаються слідами даної площини на координатних площинах 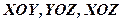– відповідно. Їх рівняння можна отримати із загального, якщо в останньому прирівняти до нуля відповідну змінну. Так, наприклад, якщо (площина ), то в цій площині рівняння сліда запишеться

.

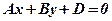Аналогічно для інших слідів.

Дата добавления: 2017-01-14