
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Канонічне та параметричне рівняння прямої
|
|
|
|
Приклад
Рівняння прямої з кутовим коефіцієнтом
Приклади.
Побудувати лінії:
а) 
б) 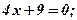
в) 
г) 
Розглянемо рівняння (1) із 3.2

Позначивши  , отримаємо
, отримаємо

рівняння пучка прямих, або рівняння прямої, що проходить через точку  у заданому напрямку. Геометричний зміст коефіцієнта
у заданому напрямку. Геометричний зміст коефіцієнта  зрозумілий з рис. 6.
зрозумілий з рис. 6.
В  , де
, де  – найменший кут, на який потрібно повернути додатний напрямок осі
– найменший кут, на який потрібно повернути додатний напрямок осі  навколо спільної точки
навколо спільної точки 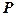 до суміщення її з прямою
до суміщення її з прямою  . Очевидно, що якщо кут
. Очевидно, що якщо кут  – гострий, то
– гострий, то 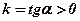 ; якщо ж
; якщо ж  – тупий кут, то
– тупий кут, то  .
.
Розкриємо дужки в (5) і спростимо його

де  . Співвідношення (6) – рівняння прямої з кутовим коефіцієнтом. При
. Співвідношення (6) – рівняння прямої з кутовим коефіцієнтом. При  – відрізок, який відтинає пряма на осі
– відрізок, який відтинає пряма на осі  (див. рис.6).
(див. рис.6).
Звернемо увагу, що для переходу від загального рівняння прямої 
 до рівняння з кутовим коефіцієнтом необхідно перше розв’язати відносно
до рівняння з кутовим коефіцієнтом необхідно перше розв’язати відносно 
 |
Рис.6

де позначено  . Якщо ж
. Якщо ж  , то із дослідження загального рівняння вже відомо, що така пряма перпендикулярна осі
, то із дослідження загального рівняння вже відомо, що така пряма перпендикулярна осі  .
.
1. Перейти до рівняння з кутовим коефіцієнтом
а)  ;
;
б)  .
.
- Скласти рівняння пучка прямих, які проходять через початок координат під кутами до осі Х: а) 30°; б) 45°; в) 120°; г)135°.
- Скласти рівняння прямих, які проходять через точку М(3,-1) під кутами до осі ОХ: а) 45°; б) 60°; в) 135°; г) 150°.
- Із точки N(5,2) під кутом 45° до осі ОХ падає промінь світла, який відбивається від осі ОХ. Знайти рівняння падаючого і відбитого променів.
Відповіді: 1. а)  ; б)
; б)  .
.
2. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
3.  : а)
: а)  ; б)
; б) 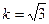 ; в)
; в)  ;
;
г)  . 4.
. 4.  ;
;  .
.
Нехай в системі координат  задана точка
задана точка  і ненульовий вектор
і ненульовий вектор  (рис.7).
(рис.7).

рис.7.
Необхідно скласти рівняння прямої, що проходить через точку  паралельно вектору
паралельно вектору 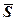 , що називається напрямним вектором. Довільна точка
, що називається напрямним вектором. Довільна точка  належить цій прямій
належить цій прямій  тоді і тільки тоді, коли
тоді і тільки тоді, коли  . Оскільки вектор
. Оскільки вектор  – заданий, а вектор
– заданий, а вектор 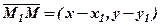 , то згідно з умовою паралельності, координати цих векторів пропорційні, тобто
, то згідно з умовою паралельності, координати цих векторів пропорційні, тобто

Співвідношення (7) називається рівнянням прямої, що проходить через задану точку у заданому напрямку або канонічним рівнянням прямої.
Звернемо увагу, що до рівняння вигляду (7) можна перейти, наприклад, від рівняння пучка прямих (4)
 ,
,
або від рівняння прямої за точкою та нормальним вектором (1)

Зауваження. Вище припускалось, що напрямний вектор 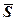 – ненульовий, але може трапитись, що одна з його координат, наприклад,
– ненульовий, але може трапитись, що одна з його координат, наприклад,  . Тоді вираз (7) формально запишеться
. Тоді вираз (7) формально запишеться

який, взагалі кажучи, не має смислу. Однак приймають  і отримують рівняння прямої перпиндикулярної осі
і отримують рівняння прямої перпиндикулярної осі  . Дійсно із рівності видно, що пряма визначена точкою
. Дійсно із рівності видно, що пряма визначена точкою  і напрямним вектором
і напрямним вектором  , перпиндикулярним осі
, перпиндикулярним осі  . Якщо ж в цьому рівнянні звільнитись від знаменника, то отримаємо
. Якщо ж в цьому рівнянні звільнитись від знаменника, то отримаємо  , або
, або  – рівняння прямої, перпендикулярної осі
– рівняння прямої, перпендикулярної осі  . Аналогічно було б отримано
. Аналогічно було б отримано  для вектора
для вектора 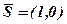 .
.
Щоб перейти до параметричного рівняння прямої, прирівняємо кожен із дробів (7) до параметра  . Оскільки хоча б один із знаменників в (7) відмінний від нуля, а відповідний чисельник може набувати довільні значення, то область зміни параметра
. Оскільки хоча б один із знаменників в (7) відмінний від нуля, а відповідний чисельник може набувати довільні значення, то область зміни параметра  – вся числова вісь. Отримаємо
– вся числова вісь. Отримаємо
 або
або 
Рівняння (8) називається параметричним рівнянням прямої.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 516; Нарушение авторских прав?; Мы поможем в написании вашей работы!