Интеграл Фурье для непериодических сигналов 1 страница

Непериодический сигнал можно рассматривать как периодический с периодом следования Т ®¥. Из выражения ω₀ = 2π/T следует, что при увеличении периода следования импульсов Т ®¥, разности частот соседних частотных составляющих спектра сигнала становятся ничтожно малыми, равными dw 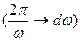. Частота близко стоящих гармоник переходит в текущее значение непрерывной частоты (kω₀→ω) и дискретный спектр частот превращается в бесконечное число бесконечно малых по амплитуде и бесконечно близких по частоте гармонических колебаний, т.е. в сплошной. Дискретная сумма в выражении (1.15) заменяется интегралом. Сигнал формируется непрерывными спектральными составляющими со своими начальными фазами

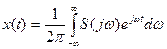, (1.19)

где

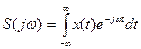(1.20)

называют спектральной плотностью или комплексным спектром непериодического сигнала x(t). Спектральная плотность определена при положительных и отрицательных частотах и характеризует распределение энергии по участкам спектра. Выражение (1.20) полностью описывает сигнал в частотной области. Сигнал (1.19) представленный во временной области, полностью определяется своим спектром и формируется непрерывными спектральными составляющими со своими начальными фазами. Эти преобразования (1.20) и (1.19) называют прямое и обратное преобразования Фурье для непериодических (одиночных) сигналов. Они связывают между собой вещественную функцию времени x(t) и комплексную функцию частоты S(jw) и их называют, соответственно, прямое и обратное преобразование Фурье.

Спектральная плотность сигнала S(jw) является комплексной величиной:

S(jw)=А(w)+jB(w), (1.21)

где , .

Модуль и фаза спектральной плотности определяются по формулам

, .

Непрерывный спектр непериодического сигнала, определяемый с помощью анализаторов спектра, также характеризуется совокуп­ностью таких важных информативных параметров как полосой частот и экстремальными значениями, по которым могут быть определены информативные параметры исследуемого непериодического сигна­ла х(t).

Результат представления непериодического сигнала интегралом Фурье:

§ спектр сигналов сплошной (непрерывный) и бесконечный;

§ спектр в общем случае является комплексным;

§ математический спектр простирается по всей оси частот от минус до плюс бесконечности;

§ физический спектр имеет место на положительной полуоси частот;

§ размерность спектра одиночных сигналов равна размерности физической величины, деленной на размерность частоты.

Рассмотрим спектральное представление типовых импульсных сигналов:

1. Спектр дельта-функции (функции Дирака). Представим единичный импульс, умноженный на постоянный коэффициент, X(t) = X_md(t). Согласно интегралу Фурье (1.19) с учетом фильтрующих свойств дельта-функции, находим

.

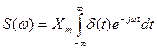При X_m = 1 спектр дельта-функции постоянный (равномерный) на всей частотной оси S(ω) =1 (рис. 1.9), т.е. содержит все частоты с одинаковой плотностью амплитуд.

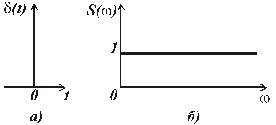
Рис. 1.9. Дельта функция: а) графическая модель, б) спектр

Взяв обратное преобразование, получим интегральное аналитическое выражение функции Дирака

d(t) = .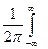

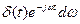2. Спектр функции включения. Пусть X(t) = X_mσ(t), тогда по преобразованию Фурье находим

S(ω) = 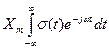= =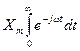πX_md(ω)+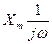

Амплитудный спектр единичного скачка гиперболический (рис. 1.10)

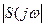= pX_md( +

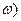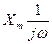
Значение спектра при ω = 0 может быть получено предельным переходом. Вместе с тем из физических соображений ясно, что среднее значение функции Хевисайда (спектр на нулевой частоте) равно половине максимального значения, так что для циклической частоты S(f) = .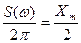

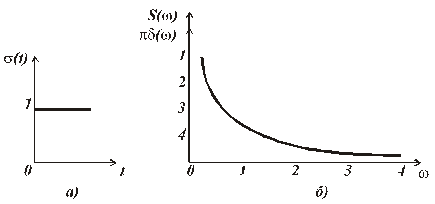
Рис. 1.10. Функция включения: а) графическая модель, б) спектр

4. Спектр прямоугольного импульса. Математическая модель прямоугольного импульса, расположенного симметрично относительно начала координат (рис. 1.11)

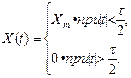
Подставив в интеграл Фурье аналитическое выражение сигнала прямоугольной формы, находим спектр

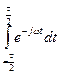S(ω) = X_m = X_{m .}

Применив формулу Эйлера, получим

S(ω) = X_mτ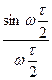

Как видно спектр комплексный, для четных сигналов он содержит только действительную часть, S(0) – вольт секундная площадь сигнала. На рис. 1.11. представлены прямоугольный импульс с единичной вольт-секундной площадью и его спектр на положительной полуоси частот. Спектр обращается в нуль в точках 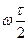= kπ, откуда ω = 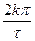. Для циклической частоты f = 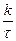в первом лепестке содержится 90% энергии сигнала, в двух лепестках – 95%. Считается, что для передачи сигнала практически без искажений, необходимо обеспечить полосу пропускания Δ f = .

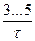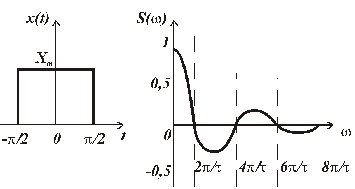
а) б)

Рис. 1.11. Прямоугольный импульс: а) графическая модель, б) спектр

5. Спектр треугольного сигнала. Аналитическое описание сигнала треугольной формы и его спектр, вычисленный по общему правилу преобразования Фурье, имеет вид (рис. 1.12)

X(t) =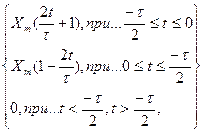

S(ω) =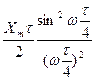

Нули спектра имеют место в точках ω-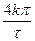

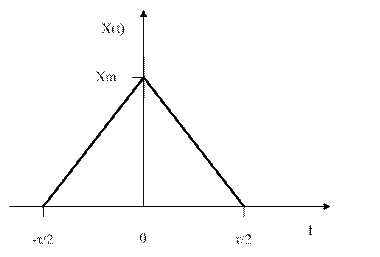
а)

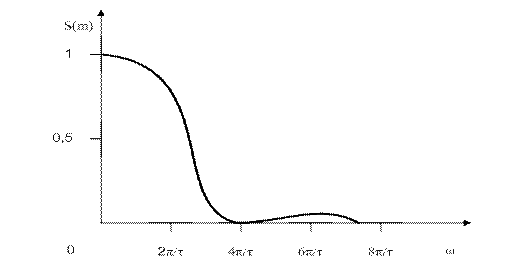
б)

Рис. 1.12. Треугольный импульс: а) графическая модель, б) спектр

6. Спектр колоколообразного импульса. Аналитическое описание импульса (гауссовского сигнала) имеет вид X(t) =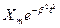

Известно, что Фурье-преобразование гауссовского сигнала приводит также к гауссовской функции. Следовательно, спектр такого сигнала:

|S(ω)| =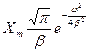

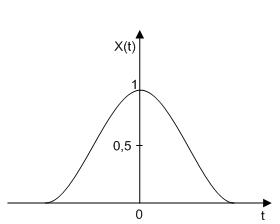
а)

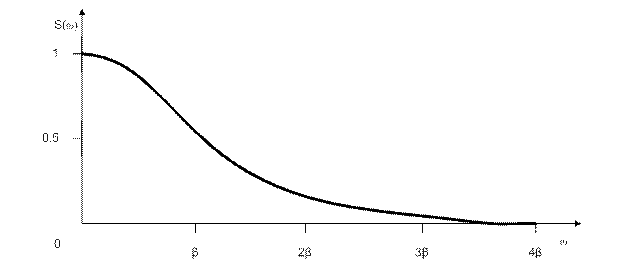б)

Рис. 1.13. Колоколообразный импульс: а) графическая модель, б) спектр

1.6. Контрольные вопросы

1. В чем принципиальное отличие измерительного сигнала от переносчика информации?

2. Какое из понятий шире сообщение или информация?

3. Представьте структурную схему получения измерительной информации.

4. Сформулируйте отличие детерминированных сигналов от квазидетерминированных.

5. Какие сигналы относят к периодическим сложным?

6. В чем отличие полигармонического сигнала от почти периодического?

7. Назовите основные статистические характеристики случайных сигналов.

8. В чем отличие стационарного эргодического процесса от неэргодического?

9. Какие сигналы относятся к основным элементарным?

10. Запишите математическую модель функции Дирака.

11. Запишите математическую модель функции Хевисайда.

12. Какими параметрами характеризуются сигналы произвольной формы, импульсные периодические сигналы?

13. Объясните механизм разложением сигнала по системе базисных функций.

14. Какие Вы знаете ортогональные базисные системы?

15. Что означает ортогональность двух функций?

16. Запишите представление сигнала обобщенным рядом Фурье.

17. Запишите экспоненциальный ряд Фурье для периодической функции.

18. Запишите математическую модель преобразований Фурье для непериодических (одиночных) сигналов.

19. Сформулируйте особенности спектров непериодических (одиночных) сигналов.

20. Приведите графическую модель спектрального представления функций Дирака и Хевисайда.

21. Приведите графическую модель спектрального представления гармонического и импульсного сигналов.

2. Виды модуляции и их применение в измерительной технике

2.1. Виды модуляции

Модуляция - это образование сигнала путем изменения параметров несущего сигнала в соответствии со значением измеряемой, (передаваемой, преобразуемой) величины. Классификацию видов модуляции можно осуществлять по основным признакам, лежащим в основе классификации самих сигналов (см. рис. 1.3), так как модуляция может выполняться без изме­нения и с изменением физического рода сигнала. Классификацию видов модуляции можно также осуществлять исходя из особенностей модулирующего сигнала и переносчика, например, учитывая характер сигналов – детерминированный, случайный стационарный и нестационарный процесс; по виду сигналов – аналоговые и дискретные; по используемому информационному параметру переносчика – амплитуда, частота, фаза, длительность, период и др.

В качестве несущего сигнала (переносчика) в информационно-измерительной технике обычно используются сигналы постоянного уровня (постоянного тока), синусоидальные сигналы (сигналы переменного тока) и последовательности прямоугольных импульсов. Тип переносчика определяет и вид модуляции.

1. Переносчик – сигнал постоянного уровня. Единственным параметром сигнала является его уровень, поэтому возможен только единственный вид модуляции – модуляция уровня или прямая модуляция. Модулированный сигнал (рис. 3.1,б), например, на выходе первичного измерительного преобразователя, в определенном масштабе повторяет закон изменения входного сигнала x(t), представленный на рис.2.1,а). При этом может изменяться и полярность напряжения. Модулированный сигнал описывается выражением

,

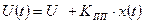где U - амплитуда сигнала постоянного уровня (на рис.2.1 не показан); 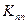- чувствительность устройства, осуществляющего процесс модуляции (первичного преобразователя).

2. Переносчик – высокочастотное синусоидальное колебание (рис.2.1,в). Так как синусоидальное колебание характеризуется тремя основными параметрами: амплитуда, частота и фаза, то существуют три основных типа модуляций: амплитудная (рис. 2.1,б,г), фазовая (рис. 2.1,б),д) и частотная (рис. 2.1,б),е). Последние два вида модуляции называют еще угловой модуляцией.

,

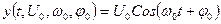где U₀ – амплитуда; 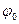- начальная фаза; 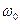- частота (несущая) невозмущенного носителя.

3. Переносчик – последовательность прямоугольных импульсов (рис.2.1,ж). На рис. 2.1 показаны модулированные сигналы при изменении трех независимых параметров – амплитуды импульсов (рис. 2.1,ж,з), смещение по фазе (или во времени) относительно исходной последовательности (рис. 2.1,ж,и) и ширины отдельных импульсов (рис. 2.1,ж,к). Возможно также осуществление частотно-импульсной и кодо-импульсной модуляции (на рис. 2.1 не показаны).

Находят применение вторичные модуляции для передачи сообщения о первично-модулированной последовательности, например, ШИМ-ЧМ, когда импульсы, модулированные по широте, подвергаются еще и высокочастотному заполнению.

Рис. 2.1. Виды модуляции

2.2. Непрерывные методы модуляции

При непрерывных методах модуляции в качестве переносчика информации используется высокочастотный гармонический сигнал, описываемый функцией

u(t) = u ₀ cos(w ₀ t + φ₀), (2.1)

где u ₀ – амплитуда, w₀ = 2p f₀ – круговая (угловая) частота, f₀ = 1/T₀ – циклическая частота, T ₀ – период, φ₀ – начальная фаза. В зависимости от изменяемого (модулируемого) параметра переносчика получают амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ) модуляции. Во всех случаях модуляция состоит в том, что модулируемый параметр переносчика получает приращение, пропорциональное изменению амплитуды модулирующего сигнала e(t). Информативный параметр переносчика при различных видах модуляции изменяется по следующему закону:

§ при АМ, как U_АМ = U₀ + ∆U e(t),

§ при ЧМ, как w = w₀ +∆w e(t),

§ при ФМ, как φ = φ₀ + ∆φ e(t)_.

Амплитудная модуляция – это образование сигнала путем изменения амплитуды невозмущенного гармонического носителя (переносчика) пропорционально мгновенным значениям напряжения или тока другого электрического сигнала (сообщения). Модулирующий сигнал может быть либо детерминированным, либо случайным, но всегда наивысшая частота его спектра W _макс должна быть меньше частоты w₀ несущего сигнала (на практике не менее чем в 10 раз).

Рассмотрим процесс модуляции, записав модулирующий сигнал, содержащий передаваемую информацию, в виде низкочастотного гармонического колебания

e(t) =E cos W t, (2.2)

где E - амплитуда модулирующего сигнала; W - частота (угловая) модулирующего сигнала.

Гармонический сигнал (2.1) запишем также в упрощенном виде

u(t) = U ₀ cos w₀t. (2.3)

В модулированном сигнале амплитуда несущей будет изменяться по линейному закону

U_АМ = U₀ + ∆U e(t), (2.4)

Аналитическое описание АМ сигнала запишется в виде:

u_АМ(t) = U_АМ cos w₀t = [U₀ + ∆U e(t)] cos w₀t = [U₀ +К E cos W t] cos w₀t =

= U₀ (1 + KE /U₀ cos W t) cos w₀t = U₀ (1 + m cos W t) cos w₀t =

U₀ cosw₀t+ 1/2 mU₀ cos(w₀ + W)t +1/2 mU₀ cos(w₀ - W)t (2.5)

где D U = KE - максимальное изменение значения амплитуды переносчика;

K - коэффициент преобразования модулятора;

m = D U / U₀ – относительное изменение амплитуды несущей, называемое индексом или коэффициентом амплитудной модуляции, характеризующим глубину модуляции.

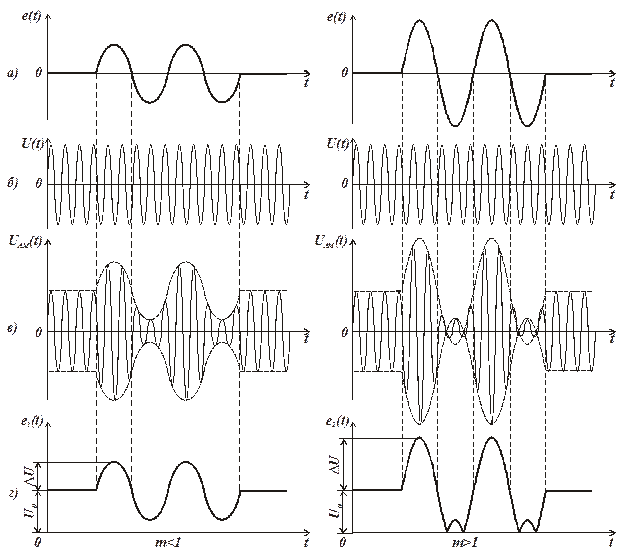
Если m £ 1, т.е. при D U < U₀, АМ сигнал всегда будет иметь положительные значения и огибающая АМ сигнала будет повторять форму модулирующего сигнала без искажений (рис. 2.2,а).

Если m > 1, т.е. при DU > U₀, структура АМ сигнала становится более сложной и огибающая АМ сигнала на выходе демодулятора уже не повторяет формы кривой сигнала e(t) (рис. 2.2,б).

Из выражения (2.5) видно, что сигнал u_AM(t) есть высокочастотное колебание, состоящее из основного колебания (2.3) и двух гармонических колебаний с частотами w ₀ ± W. Это означает, что спектр АМ сигнала состоит из трех спектральных линий (рис. 2.3,б) – линии на несущей частоте w₀ с амплитудой U ₀ и двух линий,расположенных симметрично по обе стороны от несущей, с частотами (w₀ + W) и (w₀ - W) и амплитудами, равными 1/2 mU₀. Полоса частот амплитудно-модулированного сигнала рассчитывается как D F_АМ = (w₀ + W ) - (w₀ - W ) = 2W. Следовательно, для передачи АМ сигнала требуется полоса частот, равная удвоенному значению модулирующей частоты.

а) б)

Рис. 2.2. Амплитудная модуляция: а) m £ 1; б) m > 1

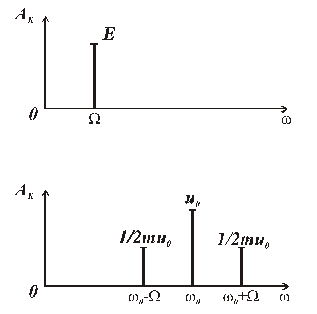
Рис. 2.3. Спектральные диаграммы: а) гармонического модулирующего сигнала, б) амплитудно-модулированного сигнала

Например, при частоте синусоидального переносчика w ₀ = 5000 Гц и частоте синусоидального модулирующего сигнала W = 100 Гц полоса частот, занимаемая АМ сигналом, будет рассчитываться как D F_АМ = 2 · 100 = 200 Гц, т.е. сигнал находится в диапазоне частот 4900 … 5100 Гц.

Мощность АМ колебания зависит от глубины модуляции. Мощность несущей частоты неизменна и пропорциональна квадрату амплитуды, т.е. u² ₀. Мощность каждого колебания с боковой частотой пропорциональна квадрату его амплитуды, т.е. m²u² ₀ /4. При m=1 (т.е. 100% АМ) мощность АМ колебания, равная сумме мощностей всех трех составляющих, в 1,5 раза превосходит мощность немодулированного колебания несущей частоты.

Рассмотрим случай, когда модулирующий сигнал e(t) – сложный периодический сигнал, записанный в виде ряда Фурье:

, (2.6)

где А_k -амплитуда k-й гармоники; φ_k – начальная фаза k -й гармоники; k = 1, 2, 3…;

Для упрощения вычислений считаем, что постоянная составляющая в сигнале e(t) отсутствует. Тогда аналогично (2.5) для АМ сигнала запишем:

u_AM(t) = [u₀ +m 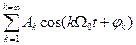] cos w₀t =

= u₀ cos w₀t + [ m 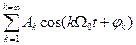] cos w₀t =

= u₀cos w₀t + ½ m + ½ m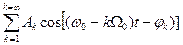

Спектр сложного АМ колебания состоит из колебаний несущей частоты w₀ и суммы колебаний с суммарными частотами (w ₀ + k W ₁) и суммы колебаний с разностными частотами (w ₀- k W ₁). Здесь(w ₀ + k W ₁) - верхняя боковая полоса, (w ₀- k W ₁) - нижняя боковая полоса. Полоса частот, занимаемая сигналом и_AM(t) в этом случае равна

D F_АМ = 2 k W₁. (2.7)

В процессе модуляции произошло смещение или перенос спектра сообщения передаваемого сигнала на интервал частот, равный частоте переносчика. Спектральные диаграммы сигналов для этого случая представлены на рис. 2.4.

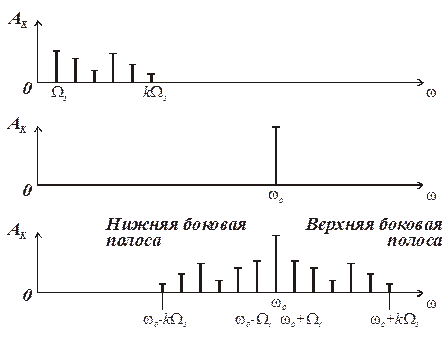
Рис. 2.4. Спектральные диаграммы сигналов при АМ модуляции

При работе нескольких измерительных устройств и в случае передачи информации от объекта измерения по одной линии связи необходимо, чтобы спектры сигналов не перекрывали друг друга, а, следовательно, чтобы несущие частоты отличались друг от друга не менее чем на 2 k W₁.

Например, если спектр сигнала ограничен частотой ·W_n =10 кГц, то ширина спектра сигнала (2.7) равна D F_АМ = 2· W _n = 20 кГц. При организации нескольких каналов несущие должны отличаться друг от друга не менее, чем на 20 кГц. Тогда число каналов связи равно

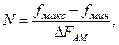
где ¦_макс - ¦_мин - диапазон частот для канала, D F_АМ - ширина спектра АМ сигнала. Например, при ¦_макс = 300 кГц, ¦_мин = 200 кГц, а D F_АМ = 20 кГц число каналов связи будет

.

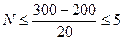В зависимости от того, передается весь ли спектр амплитудно-модулированного колебания или только его часть, различают два способа амплитудной модуляции: амплитудная модуляция с двумя боковыми полосами и однополосная модуляция. В первом случае передаваемый сигнал состоит из несущей и двух боковых колебаний (нижней и верхней боковых составляющих), т.е. передается весь спектр амплитудно-модулированного колебания.

Для уменьшения полосы частот модулированного сигнала, повышения помехоустойчивости и лучшего использования аппаратуры осуществляют передачу одной боковой полосы сигнала (ОБП), а вторая боковая полоса подавляется с помощью фильтров или специальных схем.

Возможна передача сигнала вообще без несущей частоты, осуществляемой с применением балансной модуляции. Сущность балансной модуляции (БАМ) состоит в том, что модулирующий e(t) сигнал (2.2)перемножается с колебанием несущей u(t) частоты (2.3) по формуле:

u_БАМ = u₀ e(t) cos w₀t. (2.8)

Тогда имеем:

u_БАМ (t) = u₀ E cos Ωt cosw₀t = 1/2m u₀ [cos(w₀ + W)t +u₀ cos(w₀ - W)t]. (2.9)

С математической точки зрения БАМ отличается от АМ отсутствием постоянной составляющей в исходной формуле (2.4), что приводит согласно (2.9) представления спектра состоящего 2-х спектральных линий на частотах (w ₀ + W ) и (w ₀ - W). Для восстановления передаваемого сигнала на приемном пункте необходимо добавлять несущую частоту от генератора несущих частот. Передача сигнала при этом виде модуляции позволяет уменьшить среднюю мощность передатчика.

Демодуляция, или детектирование – процесс, обратный модуляции, т.е. при амплитудном детектировании высокочастотный модулированный сигнал

u_АМ(t)= u₀ (1 + K E/u₀ cos W t) cos w₀t

преобразуют таким образом, чтобы спектр низкочастотного сигнала вернуть в область низких частот. Демодулятор состоит из амплитудного детектора и фильтра нижних частот. На выходе демодулятора получают низкочастотный сигнал, который в идеальном случае (при отсутствии погрешностей преобразования) пропорционален исходному модулирующему сигналу.

Частотная модуляции (ЧМ). При ЧМ частота синусоидального колебания (переносчика) изменяется по закону изменения амплитуды передаваемого сигнала. Выражение для частотно-модулированного сигнала запишется как

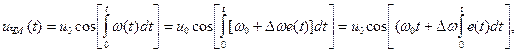(2.10)

где u₀ – амплитуда; w₀ - частота несущего колебания; Dw - максимальное отклонение частоты от w₀, пропорциональное амплитуде модулирующего сигнала.

Подставив в выражение (2.10) значение e(t) = Еcos W t, получим:

где 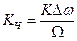^– коэффициент частотного отклонения или индекс частотной модуляции.

Спектр ЧМ сигнала получают разложением (2.10) в тригонометрический ряд. Опуская все промежуточные вычисления и переходя к пределу 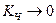получим:

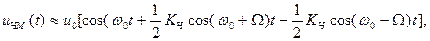(2.11)

т.е. выражение 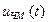при малом индексе K_Ч не отличается по спектральному составу от АМ колебания и также состоит из несущей с амплитудой u₀ и двух боковых полос (w ₀ + W) и (w ₀ - W). Полоса частот при ЧМ находится как D F_ЧМ = 2 W (K_Ч + 1). Ширина спектра при ЧМ зависит от глубины модуляции, а не от ширины спектра модулирующего сигнала как при АМ. При увеличении девиации частоты Dw при постоянной частоте модулирующего сигнала W возрастаютиндекс модуляции K_Ч и ширина спектра модулированного сигнала D F_ЧМ. Спектр ЧМ модулированного сигнала содержит несущую частоту и бесконечное число боковых составляющих. Несущую частоту выбирают из условия ω₀» (K_Ч + 1) W. С изменением частоты модуляции изменяется расстояние между спектральными составляющими. Оптимальная величина K_Ч зависит от требуемой точности передачи. Так для ИИС при выполнении измерений с погрешностью d = 1%, К _Ч = 5, а с погрешностью d = 0,1%, К _Ч = 15.

Частотная модуляция имеет ряд преимуществ перед амплитудной модуляцией. Хотя техническая реализация ЧМ сложнее АМ, и занимаемая полоса частот ЧМ значительно больше, чем при АМ, но помехоустойчивость ЧМ значительно выше, чем АМ, так как помехи воздействуют в первую очередь на амплитуду сигнала, что при ЧМ существенного значения не имеет. Мощность ЧМ колебания не зависит от модуляции, т.к. амплитуда при ЧМ постоянна. При той же мощности передатчика средняя мощность сигнала АМ оказывается меньше мощности сигнала ЧМ. Из-за плохой помехоустойчивости АМ как самостоятельный вид модуляции редко применяется, а используется чаще как промежуточный вид модуляции при двойных модуляциях типа АМ - ЧМ и ЧМ - АМ.

На приемной стороне для исключения амплитудных искажений в каналах связи частотно-модулированный сигнал предварительно усиливается и ограничивается, а затем с помощью частотного детектора выделяется полезный сигнал.

Фазовая модуляция (ФМ). При ФМ передаваемое сообщение изменяет значение фазы гармонического сигнала-переносчика в пределах девиации ∆φ. Таким образом, фаза несущей изменяется прямо пропорционально мгновенным значениям тока или напряжения модулирующего сигнала. Запишем выражение сигнала при фазовой модуляции:

Дата добавления: 2017-01-14