Интеграл Фурье для непериодических сигналов 3 страница

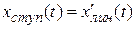(3.27)

Высота каждой ступени функции 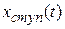равна тангенсу угла наклона прямой на соответствующем участке функции (рис. 3.2,б).

После дифференцирования функции 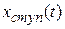получаем прибли­женное выражение для второй производной сигнала 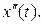Послед­няя состоит из совокупности сдвинутых во времени им­пульсных дельта-функций, «площадь» 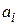каждой из кото­рых равна разности высот — смежных ступеней функции 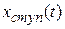в моменты .

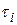. (3.28)

Принимая во внимание, что дифференцированию вход­ного сигнала соответствует дифференцирование выходного, то, определяя сумму произведений известных значений импуль­сной характеристики звена 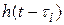на полученную совокупность импульсных дельта-функций 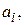получим приближенное выражение для второй производной выходного сигнала звена:

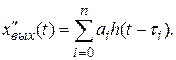(3.29)

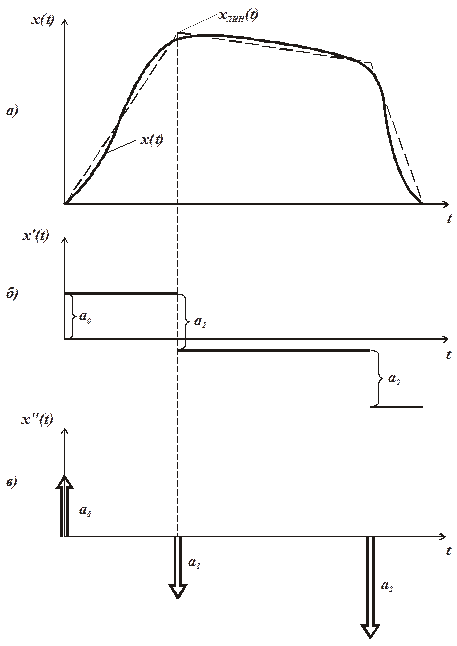
Рис. 3.2. К графоаналитическому определению интеграла свертки

Для определения искомого выходного сигнала звена 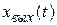дважды интегрируют выражение 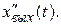При этом двойное интег­рирование производится собственно только один раз для первого участка, а выражение выходного сигнала на последующих участках определяют соответствующим сдвигом во времени и изменением коэффициента 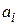. Повышение точности приближенного определе­ния выходного сигнала 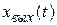можно осуществить увеличением числа интервалов при кусочно-линейной аппроксимации входного сигнала .

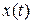Примерами линейных инерционных преобразований являются такие операции, как усиление, фильтрация, дифференцирование, интегрирование, которые описываются линейным оператором.

3.3. Преобразование измерительных сигналов в нелинейных цепях

В современных сложных измерительных устройствах все чаще становится необходимой сложная математическая обработка изме­рительной информации — для линеаризации общей характеристики измерительного прибора получения различных статистических характеристик, автоматизации косвенных измерений, сжатия дан­ных по оси значений, например в логарифмическом масштабе, и др.

Уравнение измерения, реализуемое в каждом измерительном приборе и устанавливающее зависимость между измеряемой величиной x и результатом измерения 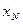, всегда линейно. Если в цепи измерительного прибора используется нелинейный измерительный преобразователь с функцией F, то для обеспечения линейности общего уравнения измерительного прибора необходимо обеспечить устранение этой нелинейности. В аналоговом измерительном прибо­ре это достигается очень просто — с помощью нелинейной шкалы, в которой реализуется обратная функция 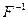. В цифровом измери­тельном приборе, цифровое отсчетное устройство которого экви­валентно равномерной шкале, устранение этой нелинейности мо­жет быть достигнуто различными структурными методами.

Возможны следующие основные структурные системы устра­нения нелинейности в цепях измерительных устройств:

ü при измерении информативного параметра выходного сигнала нелинейного измерительного преобразователя F цифровым прибо­ром с последующим преобразованием кодового сигнала в цифровом вычислительном устройстве или в нелинейном преобразователе код—код по. функции 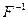(3.3,а)

ü получение требуемой нелинейной зависимости 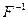в анало­говом нелинейном измерительном преобразователе и последующее преобразование выходного сигнала у линейным аналого-цифровым преобразователем (ЛАЦП) в код. При этом если аналоговый нели­нейный преобразователь входит в прямую цепь, то в нем реализу­ется функция 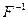, а если в обратную цепь — то функция F (3.3,б).

ü совмещение операций измерения и получения обратной нели­нейной зависимости 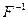в одном устройстве — функциональном аналого-цифровом преобразователе ФАЦП. При этом если данное устройство содержит только прямую цепь и основано на методе сопоставления, то в нем реализуется оператор 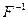. Если устройство основано на методе уравновешивания, то в его обратной цепи используется функциональный цифро-аналоговый преобра­зователь, реализующий функцию F (3.3,в).

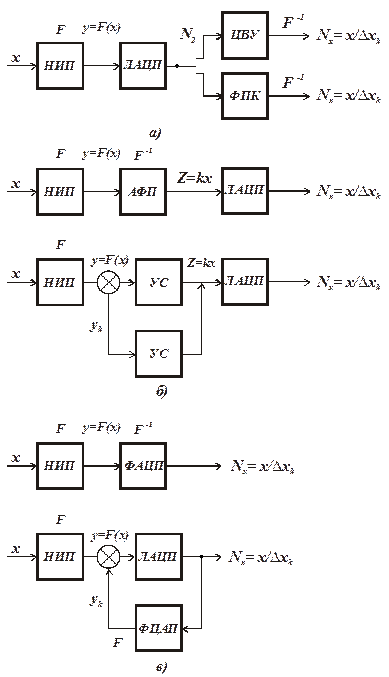
Рис. 3.3. Основные способы устранения нелинейности

При первых двух способах используются ЛАЦП, в которых значение ступени остается постоянным. При третьем способе в ФАЦП имеет место нелинейная зависимость ступени от зна­чения входной величины.

Сравнение рассмотренных структурных методов устранения нелинейности показывает, что первый способ линеаризации с циф­ровым вычислительным устройством целесообразно применять в многоканальных устройствах с большим числом параметров при большом объеме обработки по различным алгоритмам. В связи с дальнейшими миниатюризацией и снижением стоимости матрич­ных функциональных преобразователей код — код первый способ ли­неаризации становится все более перспективным и в одноканальных измерительных устройствах.

Второй способ применяется наиболее широко, так как обычно реализуется наиболее просто, с помощью аналоговых преобразо­вателей. Третий способ целесообразен при повышенных требованиях к точности преобразования.

Обеспечение линейности измерительных приборов стало нас­только насущной проблемой, что осуществляется не только струк­турными методами, но и заменой нелинейных элементов специально созданными линейными. Например, проволочные нелинейные высоко­стабильные терморезисторы заменяются высокостабильными линей­ными. Такое решение становится все более доступным, благодаря раз­витию науки о направленном изменении свойств материалов.

Нелинейное функциональное измерительное преобразование од­ного входного сигнала реализуется либо во всем требуемом диа­пазоне изменения аргумента х, либо по отдельным участкам.

Для реализации логарифмической функции применяются ана­логовые функциональные измерительные преобразователи на полу­проводниковых диодах:

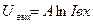(3.30)

Квадратичное преобразование тока реализуется в термоэлектри­ческих преобразователях:

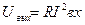(3.31)

При этом время преобразования составляет десятые доли секунды. Для мгновенного квадратичного преобразования напряжения используются кусочно-линейные аппроксимирующие устройства на полупроводниковых диодах. Для извлечения квадратного корня используются замкнутые схемы с усилителями с глубокой отрица­тельной обратной связью, в обратную цепь которых включают квадраторы на основе термопреобразователей или диод­ных аппроксиматоров.

Измерительные функциональные преобразования нескольких сигналов используются при автоматизации косвенных измерений. Широкое распространение получили измерительные функциональ­ные преобразования двух входных сигналов.

Рассмотрим реализацию метода измеритель­ного преобразования двух входных сигналов на примере трехполюсных функ­циональных измерительных преобразователей (ТИФП) в виде измерительных преобразователей мощности. Мощность зависит от двух величин — А_х (х) и А_г (х). Если известна функциональная за­висимость р=х=f(А₁;А₂), то х можно определить: косвенно, т. е. путем прямого измерения А₁(х) и А₂ (х) и после­дующего вычисления х по известной функциональной зависимости. Это, однако, требует большой затраты труда; путем использования ТИФП, в котором из двух входных вели­чин А₁ (х) и А₂ (х) создается третья промежуточная величина у, пропорциональная х:

Y = kX (3.32)

Необходимо, чтобы к в этом уравнении в минимальной степени зависело бы от внешних влияющих величин. Далеко не все величины, содержащие информацию об х, удоб­ны для подачи на входы ТИФП. В таких случаях перед ТИФП включают входные преобразователи.

В ТИФП обычно выполняются операции умножения, деления, возведения в квадрат, интегрирования и др. ТИФП применяются в ваттметрах, фазометрах, измерителях отношений — логометрах и во многих других сложных измерительных устройствах. Рассмот­рим два примера ТИФП мощности.

1. Простейшим ТИФП мощности является электродинамический измерительный механизм. В результате взаимодействия тока I в неподвижной обмотке 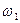и тока I 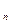в подвижной обмотке 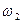создается вращающий момент М_вр = kI_нI_п 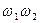cos .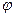

Если

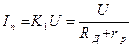, (3.33)

то

М_вр = 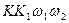IU cos 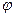= 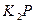(3.34 )

где U — напряжение на нагрузке, мощность которой измеряют;

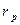— сопротивление подвижной рамки; Rд — добавочное сопротивление.

Вращающий момент закручивает противодействующую пружи­ну на угол

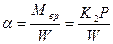, (3.33)

где W- жесткость спиральной противодействующей пружины или растяжки.

Таким образом, в результате операции перемножения в ТИФП мы получаем промежуточную величину у=а=Р. Шкала, которая устанавливается в таком измерительном устройстве, градуируется в единицах мощности. Если мощность нужно измерить при высокой частоте, на которой уже нельзя применить электро­динамический измерительный механизм, то применяют элект­ростатический или ТИФП мощ­ности на двух термопреобразо­вателях.

2. В ТИФП мощности на двух термопреобразователях реали­зуется суммо-разностный способ умножения двух переменных.

Через термопреобразователи ТП₁, и 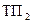, проходят токи, состоя­щие из двух составляющих 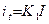и i_u = 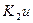, причем в ТП₁ проходит их сумма, а в ТП₂–разность. Мгновен­ные значения термо-ЭДС с термопреобразователями соответствен­но равны:

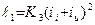
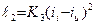(3.35)

Разность мгновенных значений термо-ЭДС е₁ и е₂ в предполо­жении идентичности и безынерционности термопар

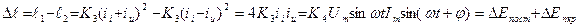
Постоянная времени термопреобразователей во много раз превосходит период 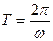, поэтому переменная составляющая 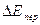почти полностью исчезает, и на выходе получаем только постоянную

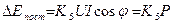. (3.36)

Таким образом, получена одна промежуточная величина Y= 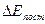= KX, пропорциональная X = Р и зависящая только от Р. 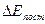измеряется высокочувствительным магнитоэлектри­ческим милливольтметром, шкала которого может быть проградуирована в единицах мощности Р.

В этом ТИФП выполняются операции возведения в квадрат, суммирования и вычитания. ТИФП является ана­логовым вычислительным устройством, реализующим функцию (а + b) 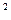— (а — b) 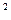= 4 аb.

Измерение активной и реактивной мощностей и энергии на про­мышленной частоте основано пока на применении ферро-динамических ваттметров и индукционных счетчиков электрической энергии. В настоящее время для измерения этих величин разрабо­тано много электронных измерительных функциональных преоб­разователей, основанных на методах широтно-импульсной моду­ляции, двойном интегрировании и др.

3.4. Контрольные вопросы

1. В чем отличие линейных цепей от нелинейных?

2. Назовите необходимые условия линейности идеальной стационарной системы.

3. В чем отличие реальной линейной стационарной системы от идеальной?

4. Назовите существующие методы анализа стационарных линейных систем.

5. Назовите основные характеристики звеньев и систем.

6. Запишите общее выражение для линейной функции преобразования физического звена измерительного канала.

7. Запишите выражение передаточной функции звена с использованием преобразований Лапласа.

8. В чем суть представления сигнала X (t) интегралом свертки?

9. В чем суть приближенного определения интеграла свертки?

10. Какое существует соотношение между частотной характеристикой линейного звена и спектром его импульсной характеристики?

11. Какие существуют структурные методы устра­нения нелинейности в цепях измерительных устройств?

4. Структуры фильтров, выбор фильтров в зависимости от измерительной задачи и методы их расчета

Задача отделения токов одних частот от токов других решается с помощью специальных устройств, называемых электрическими фильтрами. В зависимости от того, какие из частот выделяются фильтром для передачи сигнала в последующую цепь, электрические фильтры разделяются на фильтры нижних (НЧ) и верхних (ВЧ) частот. Определенное соединение НЧ и ВЧ фильтров позволяет получить полосовые (ПФ) и заградительные (ЗФ) фильтры. Задача ПФ состоит в пропускании токов с частотами, лежащими в пределах заданной полосы частот. ЗФ не пропускают токи с частотами, лежащими в пределах определенной полосы частот. Фильтры нижних частот в свою очередь делятся на две основные группы: фильтры, предназначенные пропускать токи низких звуковых частот и фильтры, предназначенные пропускать только постоянный ток.

Фильтры как устройства, осуществляющие фильтрацию сигналов, очень широко применяются в раз­личных областях техники: в электронной технике они используются практически в каждой сложной системе и приборе; в ин­формационно-измерительной тех­нике — для частотного разделения измерительных каналов, для исключения помех из смеси исследуемого сигнала и помехи, для определения частотного состава сигнала (в анализаторах спектра), для выделения основной гармоники искаженного сигнала (в измерителях нелинейных ис­кажений) и т. д.

Основной характеристикой фильтра является его частотная характеристика, имеющая сле­дующие параметры:

1) коэффициент преобразования

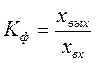; (4.1)

2) коэффициент затухания

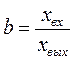; (4.2)

3) логарифмический коэффициент затухания

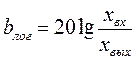; (4.3)

4) крутизна характеристики

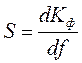; (4.4)

5) ∆f_п – частотная полоса пропускания (полоса прозрачности), которая определяется по частоте, при которой K _ф уменьшается в 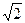раз по сравнению с максимальным значением К _ф при центральной резонансной частоте.

6) ∆f_нп – частотная полоса непропускания (полоса непрозрачности).

4.1. Структуры фильтров

Отделение постоянного тока от переменных токов может быть выполнено с помощью определенного включения R, L, C элементов. Если в цепи с постоянным и переменным током параллельно нагрузке включить конденсатор С, то при достаточно большой емкости этого конденсатора переменный ток почти весь проходит через него, а постоянный ток при этом проходит через нагрузку (рис. 4.1). Это осуществимо при условии

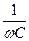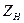
« (4.5)

Однако, в случае малого сопротивления нагрузки или очень низкой частоте переменного тока, для выполнения условия (4.5) потребуется очень большая емкость конденсатора, что приведет к увеличению габаритных размеров, массы и стоимости устройства.

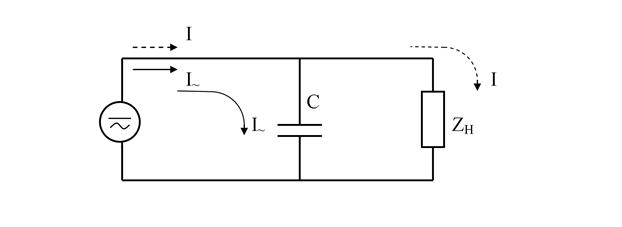
Рис. 4.1. Использование конденсатора в качестве фильтра

При малом внутреннем сопротивлении источника питания в качестве простейшего фильтра можно использовать дроссель L – катушку с обмоткой из толстого медного провода с ферромагнитным сердечником (рис. 4.2).

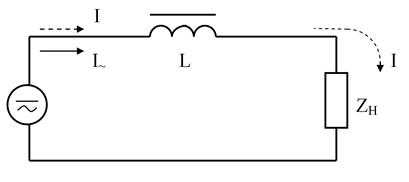
Рис. 4.2. Использование дросселя в качестве фильтра

Так как сопротивление дросселя для переменного тока велико (ωL >> z_H), то переменный ток в нагрузке окажется незначительным. Для постоянного тока сопротивление дросселя мало, поэтому он практически весь пройдет к нагрузке. Фильтр из емкости и индуктивности (рис. 4.3) называется Г – образным фильтром. Такое включение реактивных элементов позволяет значительно уменьшить наличие переменной составляющей в нагрузке Z_н. Подключив параллельно нагрузке дополнительно конденсатор С₂ (рис. 4.4), получаем П – образный фильтр. В случае резкого изменения нагрузки П – образного фильтра изменение напряжения на конденсаторе происходит сравнительно медленно, и он поддерживает напряжение на нагрузке на прежнем уровне, но зато ток в нагрузке резко изменится, т.е. П – образные фильтры позволяют получить постоянство напряжения при изменениях нагрузки.

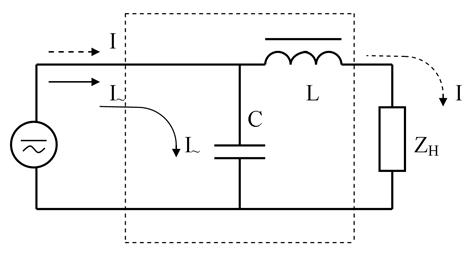
Рис. 4.3. Г- образный фильтр

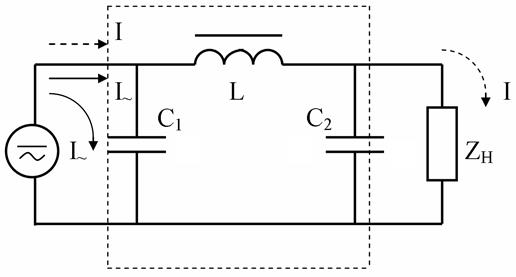
Рис. 4.4. П – образный фильтр

Включение дополнительного дросселя в цепь нагрузки Г – образного фильтра позволяет получить Т – образным фильтр (рис. 4.5). В случае резкого изменения нагрузки изменению тока в нагрузке будет препятствовать стоящий между ней и конденсатором дроссель, в котором будет индуцироваться ЭДС самоиндукции, стремящаяся поддержать ток на прежнем уровне, т.е. Т – образные фильтры обеспечивают постоянство тока на выходе при изменениях нагрузки.

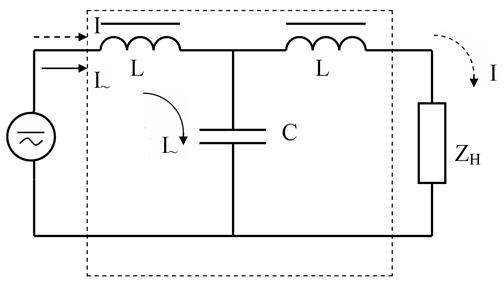
Рис. 4.5. Т – образный фильтр

К недостаткам фильтров с дросселями следует отнести большие габаритные размеры, массу и стоимость. Поэтому часто в тех случаях, когда к фильтру не предъявляется особенно жестких требований, вместо дросселей ставят резисторы (рис.4.6). Это позволяет резко сократить габариты и стоимость фильтров. Основной недостаток таких фильтров заключается в больших потерях мощности в резисторах, поэтому их используют только в тех цепях, где протекают сравнительно небольшие токи.

Рис. 4.6. Фильтры, составленные из конденсаторов и резисторов:

а) – Г – образный; б) – Т – образный; в) – П – образный.

4.2. Фильтры нижних частот

Если ставится задача пропускать только токи всех частот от нулевой до некоторой частоты f_ср1, называемой частотой среза, то для этой цели используют фильтры нижних частот, построенные по Г, П и Т – образным схемам. Создать идеальный фильтр, абсолютно не пропускающий токов, имеющих частоту выше частоты среза, практически невозможно. Реальные фильтры от идеальных отличаются тем, что крутизна их характеристик конечна; фильтры сравнивают между собой по крутизне характеристик.

Ослабление фильтруемых напряжений или токов оценивается отношением их амплитуд на выходе к амплитудам на входе (4.2). Однако чаще берется не само отношение, а его логарифм. Обычно оценку усиления (или ослабления) затухания производят в децибелах (4.3).

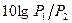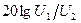
b= = (4.6)

где P₁ – мощность на входе; P₂ – мощность на выходе; U₁ – напряжение на входе; U₂ – напряжение на выходе.

На рис. 4.7 показан график затухания, создаваемого фильтром нижних частот, в зависимости от частоты подведенного к нему напряжения. Для того чтобы эта характеристика фильтра в возможно большей степени приближалась к идеальной, отмеченной пунктиром, необходимо выполнение следующих условий: сопротивление потерь в элементах фильтра должно быть минимальным, число звеньев возможно большим, сопротивление нагрузки определенным образом согласовано с параметрами фильтра.

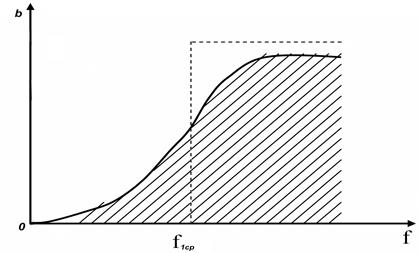
Рис. 4.7. Характеристика затухания фильтра нижних частот

Для выяснения этих условий разобьем схему любого сложного фильтра на элементарные Г – образные звенья, состоящие из емкости и индуктивности, т.е. из двух реактивных сопротивлений противоположного характера Х₁ и Х₂

(рис.4.8)

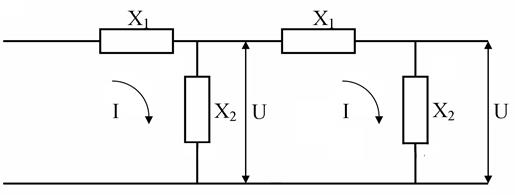
Рис.4.8. Схема фильтра, представленного в виде цепочки Г – образных звеньев

Например, при разделении Т – образного фильтра на два Г – образных звена (рис.4.9) конденсатор С₁ можно рассматривают как параллельное соединение двух конденсаторов емкостью С₁ / 2.

Рис. 4.9. Разделение Т – образного фильтра нижних частот на Г – образные звена

При разделении П – образного фильтра на Г – образные звенья (рис. 4.10) индуктивность L₁ рассматривают как последовательное соединение двух катушек индуктивностью L₁/2.

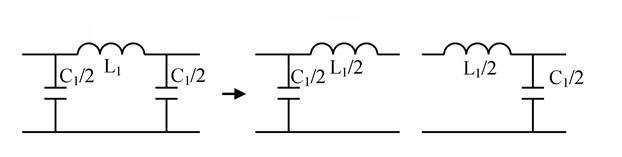
Рис. 4.10. Разделение П – образного фильтра нижних частот на две

Г – образных ячейки

Процесс передачи энергии вдоль ячеек фильтра можно представить следующим образом: переменное напряжение источника на входе возбуждает ток в первом звене фильтра, создающем переменное напряжение на элементе Х₂, т.е. на входе второй ячейки, под действием которого в ней возникает ток, и т.д. Если не учитывать потери и допустить, что вся энергия от входа передается на выход, то токи и напряжения во всех звеньях будут одинаковыми. При таком идеализированном режиме работы фильтр с нагрузкой представляет для источника чисто активное сопротивление (вся его энергия поглощается). Это возможно только в том случае, если нагрузка фильтра активная и в реактивных элементах противоположного характера протекают такие токи и действуют такие напряжения, при которых в них развиваются одинаковые реактивные мощности.

Пусть при выполнении данных условий токи во всех индуктивностях элементарных звеньев будут I, а напряжения на емкостях U. При этом реактивная мощность в индуктивности

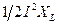
= (4.7)

а в емкости

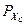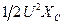= (4.8)

Из условия = 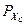можно определить, какое сопротивление будет представлять фильтр для источника питания:

R_вх = = 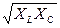(4.9)

Такое же входное сопротивление должно представлять каждое следующее звено фильтра для предыдущего. Это сопротивление называется волновым или характеристическим сопротивлением W фильтра. Подставим в уравнение (4.9) выражения для сопротивлений X _L = ωL ₁/ 2 и X_C = 2 / ωC ₁. Тогда

R_вх = W = (4.10)

Для того чтобы последнее звено работало также, как предыдущие, не-обходимо, чтобы нагрузка была согласована с фильтром, т.е. чтобы она имела чисто активный характер и равнялась волновому сопротивлению фильтра:

R_н = = W (4.11)

Каждое из Г – образных звеньев представляет собой последовательный контур. На резонансной частоте сопротивление емкостей равно сопротивлению индуктивностей. На более низких частотах сопротивление емкостей быстро возрастает, а сопротивление индуктивностей падает. Поэтому ток с частотой, которая ниже частоты резонанса, встречая малое сопротивление индуктивностей и большое сопротивление емкостей, проходит почти полностью по фильтру от источника к нагрузке. На частотах выше резонансной сопротивление индуктивностей увеличивается, а емкостей – падает. Поэтому ток с частотой, выше резонансной, встречая большое сопротивление индуктивностей, проходит через малое сопротивление емкостей и не достигает нагрузки. Резонансная частота Г – образных ячеек является частотой среза фильтра:

Дата добавления: 2017-01-14