Свойства преобразования Фурье

Преобразование Фурье в оптике «реализуется» с помощью аналогового устройства - положительной линзы, и основные свойства этого преобразования могут быть наглядно демонстрированы при рассмотрении прохождения световых волн через оптическую систему, содержащую линзы, диафрагмы, оптические транспаранты и др.

Различают прямое (2) и обратное (3) преобразования Фурье

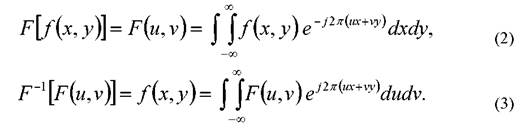
Функцию 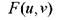, описывающую фурье-спектр исходной функции, иногда называют фурье-образом этой функции.

Преобразование Фурье линейно:

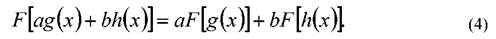
Здесь 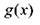и 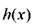- исходные функции, и 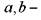постоянные

- это означает, что через одну линзу, осуществляющую преобразование Фурье, одновременно может проходить множество световых сигналов. Выполняется свойство подобия:

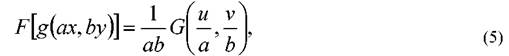
- изменение масштаба изображения на входе системы приводит к сжатию либо растяжению области его пространственного спектра.

Теорема смещения:

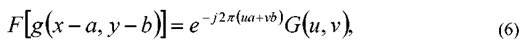
- сдвиг изображения вызывает изменение фазы спектральной функции, но сохраняет неизменной ее амплитуду. Теорема о производной:

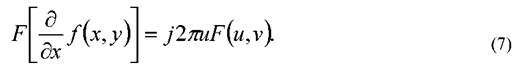
Для функций с ограниченным спектром (финитных функций) выполняется

теорема Парсеваля:

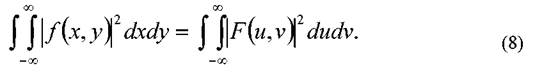
Это свойство означает постоянство полной мощности (квадрата амплитуды) излучения, проходящего через идеально прозрачную линзу.

В фурье-анализе часто используется понятие «свертка» двух функций. Свертка определяется как интеграл от произведения двух функций, смещенных друг относительно друга по осям координат, при этом величина смещения есть аргумент (независимая переменная) интеграла свертки.

Если известны преобразования Фурье двух функций,

теорема свертки утверждает, что преобразование Фурье от свертки функций равно произведению фурье-образов этих функций,

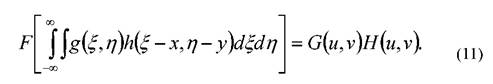
Свертку функций иногда обозначают символом ,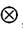

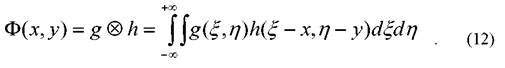
При этом теорема свертки (11) запишется кратко

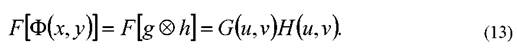
Частным случаем теоремы свертки является теорема автокорреляции,

где символ * означает комплексное сопряжение.

Выражения для свертки и автокорреляции полезны при описании действия оптических систем пространственной фильтрации изображений.

Преобразование Фурье от постоянной функции есть одна из форм представления дельта-функции Дирака,

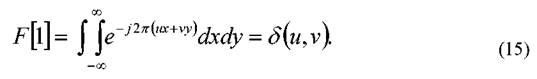
Символическая дельта-функция равна бесконечности при ее аргументе, равном нулю, и тождественно равна нулю в остальной области. Интеграл от дельта-функции конечен (обычно полагается равным единице).

Функции с постоянной комплексной амплитудой и постоянной фазой соотвествует плоская волна, распространяющаяся вдоль оптической оси. Ее спектр локализован в центре задней фокальной плоскости линзы (Рис. 2) вблизи точки фокуса линзы (нулевой пространственной частоты). Плоские волны, распро­страняющиеся под углами к оптической оси, характеризуются пространствен­ными частотами, расположенными вне фокуса линзы.

Дельта-функция описывает точечный источник света с бесконечно малыми размерами, но конечной мощностью излучения.

Обратное преобразование Фурье от дельта-функции равно постоянной,

Это выражение показывает, что пространственный спектр точечного источника света содержит бесконечный, равномерно распределенный в спектральной области, набор пространственных частот («белый шум»).

По определению, свертка дельта-функции с обычной функцией равна ее значению в точке, где дельта-функция бесконечна:

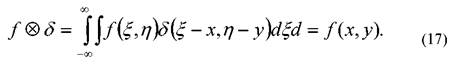
С использованием приведенных теорем выполняется двумерный частотный анализ характеристик оптических систем преобразования изображений, аналогичный спектральному анализу одномерных сигналов в радиотехнике. При этом прохождение оптического сигнала через систему призм, линз, диафрагм и т. п. аналогично прохождению электрического сигнала через электронный фильтр (четырехполюсник) с заданной амплитудно-частотной (передаточной) характеристикой.

Дата добавления: 2017-01-14