Длина волны характеристических линий и потенциал возбуждения К-серии ряда элементов. 2 страница

m= , (2.3)

где R-расстояние от эмитирующей точки поверхности до экрана. r-радиус поверхности острия. При значениях R=5см и r=50 нМ увеличение составляет 10⁶ крат.

Локальность эмиссии связана с рельефом поверхности острия. Вблизи поверхности напряженность поля не постоянна, а изменяется от точки к точке: возрастая на ребрах ступеней, террас и вершинах выступов. Наряду с этим необходимо учесть, что работа выхода электрона из кристалла существенно зависит от кристаллографического направления. Одновременное действие данных факторов, как следует из формулы (1.3), будет приводить, даже при небольших вариациях электрического поля и работы выхода, к заметному (регистрируемому по изменению интенсивности свечения) изменению эмиссии в локальных точках поверхности острия.

На рис.14.3 -15.3 приведена в качестве иллюстраций серия фотографий распределения свечения на экране для образцов различных металлов. Симметричная картина, получающаяся на экране, наглядно демонстрирует влияние кристаллической структуры металла на распределение эмиссионных точек на поверхности острия.

Четкость изображения на экране помимо технологических и «электротехнических» причин (зернистость экрана, колебания эмиссии при нестабильности высокого напряжения и др.) определяется хроматической аберрацией и дифракцией электронов. В выше приведенном схематическом описании условий формирования изображения предполагалось, что электроны, туннелирующие из металла, не имеют начальной скорости и, получая ускорение в электрическом поле, движутся строго по радиальным направлениям. В действительности эмитируемые электроны обладают небольшим разбросом в начальной энергии, и пучок траекторий, выходящих из одной точки поверхности, дает на экране не точку, а размытое пятнышко. Диаметр кружка размытия, получающегося на экране, определяется величиной разброса тангенциальной составляющей начальной скорости, и его величину, согласно теоретическим расчётам, можно оценить из равенства:

, (3.3)

где U₀-разность потенциалов, отвечающая разбросу в значении тангенциальной скорости, U-разность потенциалов, приложенная к проектору. Следовательно,

а б в г

Рис. 14.3. Электронно-микроскопическое изображение острия из торированного вольфрама на различных стадиях активации (при различных покрытиях Th на W). а). Чистый вольфрам. б). Ранняя стадия активации (после прогрева острия до 2600 К для восстановления оксида тория в толще вольфрама и последующего кратковременного прогрева при 2000 К; часть восстановленного тория диффундирует на поверхность вольфрама). в). Последующая стадия активации (прогрев при 2000 К в течении 13мин – продолжение объемной диффузии Th на поверхность вольфрама). г). Оптимальное покрытие Th на W, установившегося в результате поверхностной миграции Th (прогрев при рабочей температуре 1800 К в течение двух часов).

Рис.15.3. Автоионное изображение иридия.

разрешающая способность автоэлектронного микроскопа ограничена самим процессом формирования изображения ввиду наличия тангенциальных компонент скорости туннелирующих из образца электронов и определяется диаметром соответствующего кружка на эмиттере, т.е. величиной:

, (4.3)

получаемой по оценкам в интервале 100-300нМ. Поэтому автоэлектронный микроскоп не позволяет различать отдельные атомы, однако относительная яркость различных областей изображения (рис. 14.3 -15.3) чрезвычайно чувствительна к энергетическому электронному состоянию той области поверхности, из которой туннелируют изображающие электроны.

Рис. 16.3. Столкновение молекул изображающего газа с поверхностью острия. 1-поляризованный атом газа; 2-ионизация в поле высокого потенциала; 3- пучок эмитированных электронов.

Анализируя физические причины, ограничивающие разрешающую способность автоэлектронного микроскопа, Э.В.Мюллер делает предположение о том, что её можно улучшить только за счет массы изображающих частиц. Для подтверждения проводит ряд экспериментов с положительным, по отношению к экрану, потенциалом образца при добавлении в колбу незначительного количества водорода (переход в режим работы автоионного микроскопа) В этом случае физические процессы, приводящие к формированию изображения схематически можно представить следующей последовательностью (рис.16.3).

В сильном электрическом поле вблизи острия, атом изображающего газа поляризуется, притягивается к острию и взаимодействует с его поверхностью. В этом столкновении атом может потерять достаточное количество энергии для того, чтобы оказаться захваченным в области острия. Если это произойдет, он будет прыгать по поверхности металла, теряя энергию при каждом отскоке. В результате соударения с поверхностью захваченные атомы изображающего газа приобретают температуру острия. При медленном перелете атома, через какую либо из областей сильного поля, имеющегося над поверхностью образца, появляется вероятность того, что электрон атома изображающего газа туннелирует в металл, и атом окажется ионизированным. В сильных полях ионизация может происходить на некотором расстоянии от поверхности образца, где потенциал ниже, и, следовательно, процесс ионизации не проходит через стадию адсорбции.

На рис. 17.3,а схематически показана форма потенциала, который удерживает электрон около своего иона в отсутствии внешнего поля. При наложении электрического поля картина потенциала изменяется (рис. 17.3,б). В этом случае, если электрон туннелирует через потенциальный барьер по линии АВ, произойдет ионизация атома из основного состояния. Если атом газа находится вблизи поверхности металла, как показано на рис.17.3,в потенциальный барьер ещё более снижается за счет сил зеркального изображения, которые притягивают электрон поляризованного атома к его изображению (диполь - электрон-ион) в проводящей поверхности.

Рис.17.3. Диаграммы потенциала поля, в котором находится электрон в процессе автоионизации: а-потенциал в отсутствие поля; бпотенциал в поле ВС, в — потенциал. в поле вблизи поверхности металла с работой выхода А.

При дальнейшем приближении к поверхности, энергия электрона станет ниже уровня Ферми в металле и ввиду малой плотности состояний (тех в которые электрон может перейти) вероятность туннелирования значительно уменьшится. Это критическое расстояние определяется следующим соотношением: Х_крит.=(1- 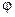)/E_r (5.3)

где Е_r-напряженность поля у поверхности острия, I-потенциал ионизации атома изображающего газа, j -работа выхода электрона из металла. Напряженность поля приближенно определяется соотношением:

E_r=U/5r. (6.3)

Первые результаты Мюллера по применению автоионного микроскопа оказались одновременно, и обнадеживающими, так как было достигнуто разрешение ≤10 нм, и разочаровывающими, поскольку не удалось различить отдельные атомы. Достигнутое предельное разрешение определялось тем, что образец находился при комнатной температуре. В то время предполагали, что процесс ионизации проходит через адсорбцию газа и последующую десорбцию в виде иона, а поэтому считалось, что разрешающая способность изображения не должна зависеть от температуры. Однако в последующих экспериментах было установлено, что при охлаждении образца до температуры жидкого азота, либо жидкого водорода и использовании в качестве изображающего газа атомов гелия, достигается атомное разрешение.

Рис. 18.3. Зависимость тока ионов гелия от приложенного напряжения, характерная для вольфрамового образца при температуре жидкого азота.

На рис. 18.3 приведена диаграмма, которая иллюстрирует типичные результаты, полученные при исследовании вольфрамового образца, с использованием в качестве изображающего газа гелия при 77К. На участке АВ с увеличением напряжения ионный ток быстро растет, а затем в узкой переходной области (вблизи точки В) возрастает линейно до тех пор, пока в точке D не будет достигнуто поле достаточное для испарения. Точку В, в которой пересекаются две экстраполированные прямые линии, можно определить как пороговую точку, а поле, соответствующее этой точке,- как пороговое поле Е_п. При полях меньших тех, которые реализуются до точки В, изображение обычно нестабильно и слишком слабо для того чтобы его можно было наблюдать или фотографировать без предварительного усиления. Следовательно, область ВD можно определить как рабочий диапазон автоионного эмиттера, а отношение испаряющего поля к пороговому полю (Е_и/Е_п ) рассматривать как величину из которой надо исходить, оценивая пригодность материала для исследования его в автоионной микроскопе. Так, например, установленные значения величины Е_и ∕ Е_п при 77 К равны: 1,7 для W, 1,35 для Мо, 1,0 для Fe и ≤1 для Ni. Испаряющее поле Е_и для каждого металла имеет свою характерную величину и при низких температурах слабо зависит от температуры. Поэтому автоэлектронный микроскоп с гелием подходит только для исследования тугоплавких металлов и сплавов с большими энергиями связи, когда Е_и/Е_п ≥2.

Испарение полем используется в начале любого эксперимента в автоионной микроскопии (тренировка образца), так как после электрохимического травления поверхность образца покрыта слоем продуктов коррозии. Этот слой загрязнений удаляется испарением при определенном значении поля. Любые неровности также устраняются, и поверхность острия приобретает рельеф необходимый для исследования. Вследствие того, что испарение полем для каждой частицы происходит при некотором характерном для неё поле, этот процесс можно точно контролировать. Отдельные атомы, группы атомов и целые атомные слои можно удалить с поверхности просто изменением приложенного к образцу напряжения. Таким образом, хотя один микроснимок дает картину расположения всего лишь нескольких атомов на поверхности, большое количество микроснимков позволяет получить трехмерную картину с образца при его «микроанотомировании» электрическим полем.

3.3. Фотоэлектронный умножитель.

Фотоэлектронный умножитель-это электронно-вакуумный прибор для преобразования слабых световых сигналов в электрические, основанный на фотоэлектронной и вторичной эмиссиях. Состоит из фотокатода, коллектора электронов (анода) и нескольких (15-20) эмиттеров вторичной эмиссии (динодов) (рис. 19.3). Напряжение на каждом диноде относительно фотокатода на (50-100) В выше, чем у предыдущего. Принцип действия электронного умножителя заключается в следующем.

Рис. 19.3. Схема работы фотоэлектронного умножителя.

Слабый электронный ток, испускаемый фотокатодом, направляется на первый эмиттер; возникающие на нем вторичные электроны ускоряются по направлению к следующему, где процесс повторяется. Если коэффициент вторичной эмиссии () каждого эмиттера, превышает единицу, то на каждом каскаде происходит усиление электронного пучка в раз, а при n каскадах общий коэффициент усиления () определится из равенства: . Для распространенных типов эмиттеров коэффициент вторичной эмиссии (при рабочем напряжении) равен 4-10, следовательно, при десяти-двадцати каскадах общий коэффициент усиления может достигать величин 10⁹-10¹¹.

Таким образом, даже отдельные фотоэлектроны создают на выходе фотоумножителя импульсы тока большой амплитуды. Интересно отметить, что при 90 каскадах один электрон дал бы 10⁵⁴ электронов, и для поддержания образующегося электрического тока не хватило бы всех электронов земного шара. В выше описанной последовательности размножения электронов предполагалось, что

а б

В

Рис. 20.3. Фотоэлектронные умножители с эмиттерами: а) в форме жалюзи (цифры внутри схемы 1-11 диноды), и б) с ковшеобразными динодами (1-8); в)-эквипотенциальные поверхности и ход электронных траекторий между ковшеобразными динодами.

все «рожденные» электроны последовательно, с каждого предыдущего эмиттера приходят на каждый последующий эмиттер без потерь, а коэффициент вторичной эмиссии для всех эмиттеров одинаков. Приближения к таким условиям обеспечивают тождественностью технологической обработки при изготовлении эмиттеров и придания им различной формы. Наиболее распространены две конфигурации: тип жалюзи (рис.20.3,а) и ковшеобразной формы (рис.20.3,б). Применение фотоумножителей в современной электронно-вакуумной технике многочисленны и разнообразны. Но наиболее успешным оказалось их применение в двух областях современной физики: это-спектроскопия и ядерная физика. При спектральных исследованиях интенсивность разложенного света нередко оказывается малой и недоступной для фотографической регистрации, поэтому применение фотоэлектронных умножителей приносит здесь неоценимые преимущества. В ядерной физике фотоумножители применяются как для регистрации частиц, так и для определения их энергии. Прибором для регистрации является сцинтилляционный счетчик, представляющий собой комбинацию фотоэлектронного умножителя с люминофором (рис.21.3), а принцип его работы заключается в следующем. Быстрая частица, проходя через кристалл люминофора, наряду с ионизацией атомов и молекул возбуждает их. Возвращение, после возбуждения, в основное состояние сопровождается (световой вспышкой) испусканием фотонов. Световая вспышка регистрируется фотокатодом умножителя, (рис.21.3.) который находится в оптическом контакте с кристаллом. Фотоны, попадая на катод фотоэлектронного умножителя, выбивают электроны, в результате чего на его коллекторе возникает электрический импульс, который далее регистрируется и усиливается.

Рис.21.3. Принципиальная схема сцинтилляционного счетчика с применением светопровода между кристаллом и катодом фотоумножтеля. 1-2-эмиттеры фотоумножителя.

Кратковременность вспышки позволяет вести регистрацию частиц при очень высокой скорости счета. Если пробег частицы укладывается в кристалле, то величина световой вспышки в широком интервале энергии оказывается монотонной и приблизительно линейно возрастающей функцией энергии, Это обстоятельство позволяет использовать подобные устройства не только как счетчики, но и как сцинтилляционные спектрометры.

Для того чтобы световая вспышка была зарегистрирована, необходимо, чтобы спектр излучения сцинтиллятора совпадал со спектральной областью чувствительности фотоэлектронного умножителя, а сцинтиллятор был прозрачен для собственного излучения. Доля энергии регистрируемой частицы, которая превращается в световую энергию, называется конверсионной эффективностью (. Наибольшими обладают кристаллы NaJ, антрацена и ZnS. Интенсивность свечения после прохождения частицы изменяется во времени экспоненциально:

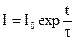, (7.3)

где: I₀-начальная интенсивность, -время высвечивания, определяемое временем жизни на возбужденных уровнях.

Для большинства сцинтилляторов величина, Чем меньше величина , тем более быстродействующим является сцинтилляционный счетчик. Самым малым обладают пластмассы.

Вопросы для самопроверки.

1. Какие физические процессы вызывают появление тормозного и характеристического рентгеновского излучения.

2. От чего зависит интенсивность тормозного и характеристического излучения. Какими физико-химическими параметрами ограничивают проникающую способность рентгеновских лучей.

3. Объясните разницу между рентгенологическим, рентгеноструктурным и рентгеноспектральным методами анализа.

4. Сформулируйте требования к образцу для исследования в электронно-ионном проекторе. Что такое тренировка образца, и какими физическими процессами она сопровождается.

5. За счет, каких физических процессов формируется изображение в электронном проекторе. Какими физическими процессами ограничена разрешающая способность прибора.

6. За счет, каких процессов формируется изображение в ионном проекторе. Почему разрешающая способность ионного проектора на порядок выше, чем электронного.

6. От чего зависит коэффициент усиления ФЭУ.

7. Что такое конверсионная эффективность сцинтилляционного кристалла.

8. Назовите области применения сцинтилляционных счетчиков.

Глава 4

ТЕОРИЯ И ПРАКТИКА ФОКУСИРОВКИ И УПРАВЛЕНИЯ ЭЛЕКТРОННЫМИ ПУЧКАМИ В ЭЛЕКТРОМАГНИТНЫХ ПОЛЯХ.

1.4.Силы, действующие на заряженную частицу в электромагнитном поле. Уравнения движения.

Электромагнитные поля в вакууме полностью описываются двумя силовыми характеристиками: вектором напряженности электрического поля Е и вектором магнитной индукции В. Как напряженностьполя так и магнитная индукция являются векторными функциями пространственных координат и времени Е = Е (R,t) [В/м], В = В (R, t) [Вс/м²], где R -радиус вектор, t-время.

Согласно экспериментальным данным на заряженную частицу в рассматриваемой области электромагнитного поля действует сила F, выражаемая формулой:

F =q E +q[ v × B ], (1.4)

где q-заряд частицы, v -вектор скорости частицы. При этом формула справедлива только при следующих условиях:

1. Размеры частицы настолько малы, что её заряд можно считать точечным. Это позволяет не учитывать дополнительные силы, связанные с распределением заряда по объёму частицы.

2. У частицы отсутствует собственный магнитный момент.

3. В формуле (1.4) пренебрегается силой лучистого трения, которая делается заметной при большой величине ускорения, приобретаемого частицей в электромагнитном поле.

4. Движение заряженной частицы в электромагнитных полях, при скоростях меньше чем скорость света определяется, законами классической механики. Естественно, что волновая природа частиц является существенным ограничением при характерных размерах, сравнимых с длиной волны Де Бройля:

l= . (2.4)

Здесь h=6,62×10^-34Дж c постоянная Планка. m - масса заряженной частицы.

Однако при анализе движения частиц волновой природой можно пренебречь, так как электромагнитные поля не претерпевают существенных изменений на расстояниях, сравнимых с длиной волны Де Бройля.

Согласно законам классической механики уравнение движения частицы в заданном поле может быть написано в обычной форме:

(m v)= F. (3.4)

При условии, когда скорость движения частицы меньше скорости света масса частицы постоянна то уравнение (1.4) с учетом (3.4.) принимает вид:

m (v)=q E+ q[ v × B ]. (4.4)

Первое слагаемое в правой части уравнения представляет собой кулоновскую силу, действующую на заряженную частицу со стороны электростатического поля. Кулоновская сила, действуя на заряженную частицу, совершает работу, изменяя кинетическую энергию частицы, так как она изменяет скорость движения частицы по величине. Изменение кинетической энергии частицы, обусловленное только действием электростатического поля можно определить из равенства:

()₂ - ()₁= E d s, (5,4)

где интеграл берется вдоль траектории движения частицы. Если электрическое поле обладает потенциалом, который не зависит от времени, то правая часть уравнения (4.5) будет равна q(U₁-U₂). Для частицы, которая первоначально находилась в покое, формула (5,4) приобретет вид уравнения:

=q(U₁-U₂), (6.4)

из которого следует, что при движении в статическом потенциальном электрическом поле кинетическая энергия заряженной частицы определяется пройденной разностью потенциалов.

В физике, как правило, приходится иметь дело с частицами, заряд которых составляет небольшое целое кратное от заряда электрона. Отсюда вытекает распространенный способ измерения энергии частицы в электрон-вольтах. Если заряд частицы равен заряду электрона (е) и она прошла ускоряющую разность потенциалов в один вольт, то говорят, что она приобрела энергию в один электрон-вольт равный 1,6×10^-19 Дж. Очевидно, что частица с зарядом (ne), ускоренная разностью потенциалов (U₁-U₂) вольт, будет обладать кинетической энергией Е_к равной:

Е_к=n(U₁-U₂) эВ. (7.4)

Последняя формула дает связь между пройденной разностью потенциалов и кинетической энергией частицы выраженной в электрон-вольтах.

Второе слагаемое в правой части уравнения (4.4) сила Лоренца, действующая на частицу со стороны магнитного поля. По определению векторного произведения вектор силы Лоренца всегда направлен перпендикулярно вектору скорости частицы, а, следовательно, данная сила работы не совершат. Данная сила играет роль центростремительной силы и изменяет скорость движения частицы только по направлению.

Анализ движения заряженных частиц в электромагнитных полях при использовании уравнения (4.4) не представляет значительных математических трудностей только для полей простейшей конфигурации (точечного заряда, заряженного цилиндрического проводника, плоского конденсатора, однородного магнитного поля в соленоиде и др.). Однако в практике проектирования электронно лучевых приборов электромагнитные поля оказываются настолько сложными, что даже выражение для потенциала и вектора магнитной индукции не удается представить в конечной форме с помощью элементарных функций. В результате интегрирование уравнений движения чрезвычайно усложняется и в итоге, может быть проведено только численным путем. Общий метод подхода к решению задач о нахождении траекторий движущихся заряженных частиц в электрических и магнитных полях различных конфигураций оказывается возможным только с использованием современного математического аппарата электронной и ионной оптики.

Электронная и ионная оптика представляют собой одно из направлений физической электроники посвященной проблемам: формирования потоков заряженных частиц, управления ими, а также вопросам их применения. В самом названии «Электронная и ионная оптика» отражен тот факт, что движение заряженных частиц в электромагнитных полях во многом подобно поведению световых лучей в неоднородных оптических средах описываемых законами геометрической оптики.

2.4. Аналогия между движением заряженных частиц в электростатическом поле и распространением световых лучей в прозрачной среде.

С учетом того, что заряд электрона отрицательный, уравнение движения нерялетивисткого электрона в электростатическом поле с потенциалом U( описывается уравнением:

m . (8.4)

При условии равенства потенциала U=0 там, где электрон имеет нулевую скорость, кинетическая энергия определится из равенства:

, (9.4)

а, следовательно, абсолютная величина скорости электрона определяется уравнением:

v= , (10.4)

из которого следует, что электрон может находиться только в областях пространства, где U( ≥0.

Предположим, что электрон из полупространства z≤0, где потенциал U( постоянен и равен U₁ (рис. 1.4), перелетает в полупространство z≥0, где потенциал также постоянен и равен U₂. Скачку потенциала на линейной границе раздела соответствует бесконечно большая величина напряженности поля и в принципе, получить такой скачок потенциала технически невозможно. Наилучшим физическим приближением в этом случае будет система, состоящая из двух близко расположенных чрезвычайно тонких металлических фольг, прозрачных для рассматриваемых частиц.

Рассмотрим, что происходит с траекторией электрона при переходе через границу. Вектор скорости электрона разложим на два составляющих: _n – нор-

Рис.1.4. Преломление траектории электрона при переходе через скачок потенциала.

мальный (перпендикулярный) к границе раздела сред (z) и _t- тангенциальный (параллельный) к границе раздела. Поскольку

, (11.4)

то силы тангенциальные к границе раздела (z=0) отсутствуют, а, следовательно, тангенциальная составляющая скорости согласно уравнению (9.4) остается неизменной. Напротив нормальная составляющая скорости возрастает, так как, проходя через границу раздела (z=0) электрон, испытывает только действие силы, направленной по нормали к границе раздела:

|e| ₂-U₁) (z). (12.4)

Полную скорость до и после прохождения через поверхность раздела (z=0) можно определить из равенства (рис. 1.4):

v = , (13.4)

а её изменение можно вычислить по формуле:

v_1,2= (14.4)

Из равенства тангенциальных составляющих вектора скорости электрона (рис. 1.4), v_t,1=v₁sina до и v_t,2=v₂sinb после прохождения границы раздела следует:

Дата добавления: 2017-01-14