Длина волны характеристических линий и потенциал возбуждения К-серии ряда элементов. 4 страница

Рис. 9.4. Схема расположения и питания электродов многоэлектронных пушек.

Отличительной чертой тетродных (четырехэлектродных) и пентодных (пяти электродных) пушек (рис.9.4) является независимость величин, характеризующих модуляции тока (изменение электронного тока по величине), от положения и размеров кроссовера. Такие пушки называют электронным прожектором.

Особенностью устройства для фокусировки и управлением интенсивностью электронного пучка, в электронном прожекторе является наличие главной проекционной линзы образованной двумя цилиндрическими электродами (рис. 9.4) анод 1 и анод 2. Данная линза прожектора по отношению к катоду настраивается таким образом, что на экране формируется не изображение катода электронной пушки, а изображения места пересечения лучей (рис.9.4) в пучке, т.е. места его максимального сжатия. Модуляция пучка по интенсивности меняется изменением напряжения на электроде Венельта. Если на электрод Венельта подано значительное отрицательное напряжение (в практике ≤ 40 В), относительно ка- тода, то электрическое поле вдоль всей поверхности катода является тормозящим (рис. 11.4,а), и ток в пучке равен нулю. По мере постепенного повышения потенциала «седловина» на потенциальном барьере (рис. 11.4, б) приближается

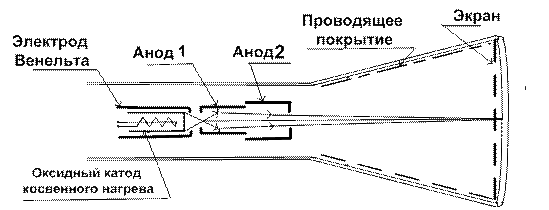
Рис. 10.4. Схема устройства и формирования электронного пучка в электронном прожекторе.

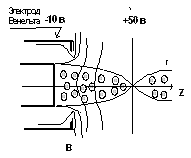к катоду и при некотором значении Uв эквипотенциальная поверхность коснется катода. В этом случае на поверхности катода возникает небольшая область с ускоряющим полем перед ней и, в этот момент, появляется ток пучка (рис 10.4,б). При дальнейшем возрастании потенциала все больший участок катода начинает принимать участие в эмиссии электронов, все больших значений

Рис. 11.4. Модуляция электронного пучка по интенсивности изменением потенциала на электроде Венельта.

достигает ускоряющее поле у поверхности катода, и ток электронного пучка возрастает (рис.11.4,в). Таким образом, вариация напряжением смещения позволяет осуществлять модуляцию электронного пучка в широких пределах.

Изучение конструкций сильноточных электронных пушек и схем формирования и управления электронным лучом выходит за рамки программы настоящего пособия. Однако целесообразно отметить следующее. Из многообразия технологических высокоточных пушек электронных пушек с различными сочетаниями параметров можно выделить следующие большие группы:

1. Электронные пушки большой мощности (10⁵ - 10⁶ Вт) с уровнем ускоряющего напряжения до 50 кВ и плотностью мощности до 10 Вт/см², применяемые в основном для плавки, литья и испарения материалов в непрерывном режиме.

2. Электронные пушки средней и малой мощности (10³ - 10⁵ Вт) с уровнем ускоряющего напряжения до 60 кВ и плотностью мощности пучка 10³ - 10⁷ Вт/см², применяемые в основном для электронно-лучевой сварки, а также наплавки и термообработки.

3. Импульсные электронные пушки нано - и микросекундного диапазона, применяемые для термо- и других видов обработки.

5.4.4. Электростатические системы управления электронным лучом.

Пучки заряженных частиц можно не только фокусировать в электростатических полях, но также отклонять, изменять их диаметр и определять их скорость.

Простейшим элементом для управления электронными пучками является плоский конденсатор (рис. 12.4). Электростатическое поле внутри такого конденсатора однородно. Однако вблизи его краев поле становится слабее и изгибается (рис. 12.4) в окружающее пространство, поскольку теоретически поле исчезает только на бесконечном расстоянии от конденсатора. Если расстояние между обкладками конденсатора равно (d), то поле внутри конденсатора можно считать практически однородным до этого расстояния от края. Таким образом, реальный конденсатор можно заменить идеальным с эффективной длиной, несколько большей, чем реальная длина l. Хотя такой идеальный конденсатор не реализуем, поскольку однородное поле не может внезапно исчезнуть, однако такая простая модель является хорошим приближением при описании реального прибора.

Наиболее важным практическим применением плоского конденсатора в электронной и ионной оптике является его использование для отклонения заряженных частиц образующих электронный луч.

При вхождении в конденсатор электронов, образующих пучок, со скоростью:

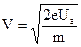, (25.4)

где U_a ускоряющая разность потенциалов в промежутке катод – анод, на электроны начинает действовать кулоновская сила: со стороны электростатического поля конденсатора F =e E, направленная перпендикулярно к вектору начальной скорости. Под действием этой силы вектор скорости изменяет направление, и электроны начинают участвовать в двух видах движения. Равномерном, со скоростью V_z, вдоль оси (z) и равноускоренным со скоростью V_y вдоль оси (Y) (рис. 13.4). Уравнение движения для электронов (слагающих пучок) вдоль оси Y:

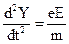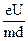= , (26.4)

где Е - напряженность поля конденсатора, U – разность потенциалов на обкладках, d – расстояние между пластинами конденсатора. После двукратного интегрирования получим уравнение:

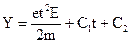, (27.4)

в котором, исходя из начальных условий, постоянные интегрирования С₁=С₂=0.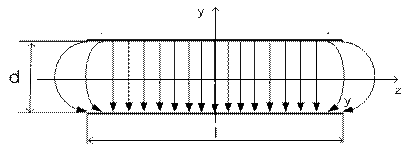

Рис. 12.4. Электростатическое поле плоского конденсатора.

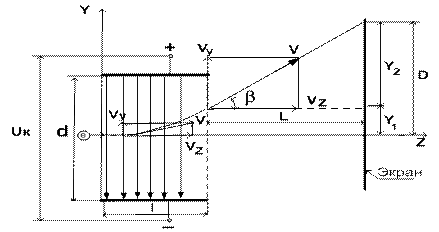
Рис.13.4. Траектория электронного луча в электростатическом поле плоского конденсатора.

Подставляя в (27.4) время прохождения электронами в пространстве конденсатора расстояния (l) при скорости движения определяемой равенством (25.4) получим уравнение:

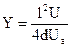, (28.4)

определяющее величину отклонения электронного пучка от оси z при выходе из конденсатора. Электроны, выйдя из конденсатора, продолжают двигаться по прямой (рис.13.4) направленной под углом b к оси z, а, следовательно, тангенс угла отклонения определится как:

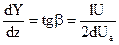. (29.4)

Величина отклонения электронов (D рис. 13.4), образующих пучок, в плоскости экрана от оси (z) определяется равенством:

D=Y₁+L tgb, (30.4.)

после подстановки в которое (29.4) получим:

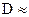
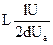. (31.4)

Для характеристики отклоняющей системы электронно-лучевых приборов вводится понятие чувствительности электронно-лучевой трубки, которая определяется величиной отношения:

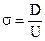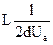= . (32.4)

Из выражения (32.4) следует, что чувствительность трубки не зависит от заряда частицы. Ни величина отклонения, ни наклон траектории не зависят от отношения заряда к массе частицы. Электроны либо ионы разных масс отклоняются на одну и ту же величину, если они ускорены одинаковым напряжением (хотя скорости сами по себе различны для частиц разной массы, формула 25.4).

Таким образом, одна и та же электростатическая отклоняющая система может быть использована для любой заряженной частицы, что очень удобно при работе с ионными пучками.

Для увеличения чувствительности необходимо:

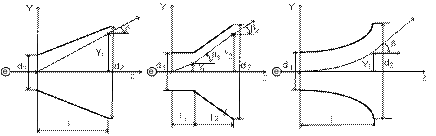
Рис.14.4. Форма отклоняющих пластин.

1. Уменьшать ускоряющее напряжение U_a, но это приведет к уменьшению яркости пучка.

2, Увеличивать длину пластин конденсатора (l), но при этом увеличиваются размеры трубки.

3. Увеличивать длину пластин (l) и уменьшать расстояние (d) между ними. Однако такой вариант приемлем при условии, чтобы при максимальном отклонении электронный луч не попадал на пластины. Поэтому на практике часто применяют пластины с отогнутыми краями (рис. 14.4). В современных электростатических лучевых трубках чувствительность составляет 0,1 – 0,2 мм/В.

В электронно лучевых трубках для управления пучком электронов обычно используют две пары пластин, разделенных и повернутых по отношению друг к другу на 90⁰ относительно оптической оси (z) (рис.15.4).

Однако в некоторых случаях более удобным, оказывается, использовать большее число простых электродов, поддерживающих соответствующие потенциалы для получения любой конфигурации электростатического поля. На рис.16.4 показано, как расположить восемь электродов, чтобы получить два взаимных перпендикулярных дипольных поля. Это так называемый «октупольный дефлектор».

Такое расположение электродов обладает несколькими преимуществами при сравнении с двумя парами пластин, разделенных и повернутых по отношению друг к другу на 90⁰ относительно оптической оси (z).

Рис.15.4. Отклоняющая система из

двух плоских конденсаторов.

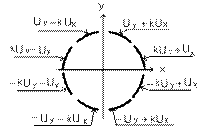
Рис. 16.4. Электростатический

октупольный дефлектор.

1. Оно более компактно и имеет меньшие аберрации. 2). Может быть использовано одновременно как стигматор. 3) Это поле легче вычисляется, чем поле от плоских конденсаторов.

Соотношение между потенциалами электродов, необходимых для надлежащего действия восьми электродного отклоняющего устройства (дефлектора)

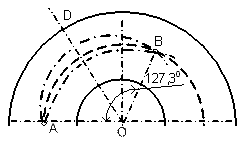
Рис. 17.4. Фокусировка пучка заряженных частиц в

электростатическом поле цилиндрического конденсатора.

представлены на рис. 16.4. Символами U_x и U_y обозначены потенциалы, используемые для отклонения в направлениях х и у соответственно. Результирующие напряжения являются суперпозицией этих двух потенциалов, взвешенных параметром k, который в итоге и определяет распределение потенциала в плоскости х-у (0≤k≤1). Его величина влияет на чувствительность отклонения и аберрации.

Для фокусировки и отклонения плоских пучков более удобным оказывается использование электростатического поля создаваемого цилиндрическим конденсатором (рис. 17.4). В таком поле могут существовать траектории частиц, совпадающие с эквипотенциальными линиями. Для плоского пучка эти траектории представляют собой окружности. Заряженные частицы будут двигаться внутри конденсатора вдоль окружности радиуса R₀, если удовлетворяется условие:

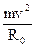=qE(R_o). (33.4)

В поле цилиндрического конденсатора:

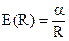, (34.4)

где постоянная 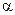определяется разностью потенциалов U, приложенной между пластинами конденсатора:

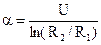, (35.4)

а R₁ и R₂ радиусы пластин.

С учетом (35.4) условие (33.4) можно записать в следующем виде:

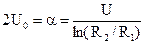. (36.4)

Для заряженных частиц, удовлетворяющих этому условию, любая окружность в пространстве между пластинами конденсатора является возможной траекторией, если начальная скорость частицы направлена вдоль окружности (рис.17.4).

Вывод уравнения траектории заряженных частиц в цилиндрическом конденсаторе базируется на полярных координатах и выходит за рамки настоящего курса программы. В связи с этим отметим только некоторые следствия, вытекающие из получаемого уравнения траектории:

U=U₀sin 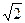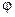. (37.4)

Угол 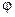отсчитывается от линии ОА (рис. 17.4).

1. Пучок заряженных частиц, источником которого является точка А (рис.17.4), находящаяся внутри конденсатора, будет сфокусирован в точке В после поворота на угол, равный 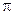/ 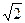, т.е. на 127,3⁰.

2. Если разрезать конденсатор по линии ОД (биссектриса угла 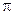/ 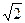) и удалить его вторую часть, то выходящий из конденсатора пучок будет параллельным. Отсюда следует, что параллельный пучок, входящий в цилиндрический конденсатор, будет сфокусирован после поворота на угол 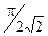, т.е. на угол 63,6⁰.

В общем случае цилиндрический конденсатор, расположенный на пути заряженного плоского пучка с достаточно малой угловой расходимостью, ведет себя как некоторая комбинация цилиндрической линзы, и призмы поворачивающей пучок. Эти свойства полей рассматриваемого типа широко применяются в масс-спектроскопии, (разделении изотопов).

6.4.4. Анализатор скорости заряженных частиц.

Если при движении частицы с зарядом q в однородном электростатическом поле компонента скорости v_х по направлению противоположна электростатической силе, то для положительно заряженной частицы v_o<0, а для отрицательно заряженной частицы v₀>0. Электростатическое поле в этом случае будет замедлять частицу до тех пор, пока она не столкнется с электродом или же не изменит направление движения и будет ускорена по направлению к противоположному электроду.

Пусть положительно заряженная частица начинает движение от отрицательного электрода с наибольшим абсолютным значением потенциала, причем v_х-компонента направлена к другой обкладке. Сможет ли данная частица достичь этой обкладки?. Да, если компонента скорости v_х достаточно велика, чтобы противодействовать электростатической силе, пока частица пройдет расстояние d в направлении х (рис. 12.4). Следовательно, в случае v_0y=v_0z=0, когда частица движется перпендикулярно обкладкам, её начальная кинетическая энергия должна быть больше величины qDU, то есть частица может достигнуть противоположной обкладки при условии:

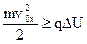. (38.4)

Частицы с меньшей кинетической энергией будут остановлены (и ускорены в противоположном направлении), прежде чем они достигнут противоположной обкладки. Если имеется источник заряженных частиц с разными кинетическими энергиями, то можно измерить распределение частиц по энергиям (скоростям), непрерывно изменяя напряжение на конденсаторе и измеряя ток, проходящий через положительную пластину с небольшим потенциалом. Очевидно, что при любом значении DU этот ток пропорционален числу частиц с начальной энергией, превышающей qDU.

7.4.4. Осциллографическая трубка.

В ходе физического эксперимента измеряемые физические величины (температура, давление, переменный ток, световой поток и т. д.) как правило, изменяются со временем. При наличии датчиков позволяющих преобразование параметров указанных величин в соответствующие электрические импульсы их можно зарегистрировать на экране электронного прожектора в зависимости от времени практически без искажения. В этом случае электрические импульсы, описывающие временной ход изучаемой величины, подаются на отклоняющую систему, которая состоит из двух пар взаимно перпендикулярных X и Y отклоняющих пластин (плоский конденсатор рис. 15.4) размещенных в электронном прожекторе между вторым анодом и экраном.

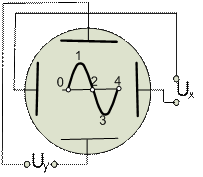
а б

Рис. 18.4. Схема получения осциллограммы

на экране электронно-лучевой трубки.

Для наблюдения на экране электронного прожектора временных диаграмм (осциллограмм) к X-пластинам трубки подводится напряжение пилообразной формы (рис.18.4,а). Если напряжение на Y-пластинах отсутствует (U_y=0), то светящаяся точка на экране с постоянной скоростью будет совершать колебательное движение (перемещаться по экрану из точки 0 в точку 4 по прямой линии рис. 18.4,б). При этом, если период пилообразного напряжения Т_y ≤ 0,1 секунды, то на экране будет просматриваться не бегущее пятно, а прямая светящаяся линия, что объясняется инертностью нашего зрения.

При подаче на Y – пластины исследуемого периодического сигнала измеряемой величины, электронный луч (светящееся пятно на экране) начнет отклоняться и в вертикальном направлении. Если исследуемый сигнал будет гармоническим колебанием с периодом Т_у = Т_х (рис. 18.4,а), то при совместном воздействии на электронный луч отклоняющих напряжений светящееся пятно в пределах каждого периода Т_х будет перемещаться на экране по криволинейно траектории 0,1,2.3,4 воспроизводящей в соответствующем масштабе форму исследуемого сигнала, называемого осциллограммой. Для получения устойчивого изображения на экране необходимо строгое выполнение равенства (синхронизации) Т_х=nТ_у, где n-целое число, соответствующее количеству наблюдаемых на экране периодов исследуемого сигнала.

Для того чтобы на экране не просматривался обратный путь светящегося пятна при его движении из точки 4 в точку 0, электронный луч на это время «гасится» отрицательным импульсом напряжения, подаваемого на электрод Венельта, обеспечивающем Uв ≥ U_max . Для точного воспроизведения осциллограммы необходимо, чтобы отклонения луча происходило прямо пропорционально приложенным к пластинам отклоняющим напряжениям, т.е. чтобы чувствительность трубки (отдельно для X и Y пластин) во всех точках экрана была одинаковой. Ранее отмечалось, что чувствительностью электростатической трубки называют величину определяемую отношением величины отклонения светящегося пятна от центра экрана (D) к величине отклоняющего напряжения. Ввиду искажения электрического поля на краях отклоняющих пластин по причине взаимного влияния полей между пластинами и вторым анодом чувствительность трубки по центру и по краям оказывается неодинаковой. Поэтому в практике конструирования приборов хорошего воспроизведения добиваются специальной конфигурацией пластин (рис. 14.4) при которой компенсируются краевые эффекты.

5.4. Фокусировка и управление потоком заряженных частиц в постоянных магнитных полях.

Вектор силы Лоренца, действующий на заряженную частицу в постоянном магнитном поле, по определению векторного произведения:

F _л=q[ v × B ], (38.4)

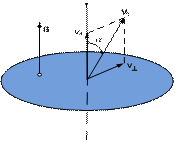
Рис. 19.4. Составляющие начальной скорости

частицы, движущейся в магнитном поле.

перпендикулярен вектору скорости частицы. Поэтому движение частицы влетающей в магнитное поле с вектором скорости (v) под углом (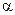) к вектору магнитной индукции (В) распадается на два вида движения: а) равномерное вдоль оси (z), совпадающим с направлением вектора индукции магнитного поля; и б) движения в плоскости перпендикулярной к вектору В (рис. 19.4). Сила Лоренца непрерывно поворачивает, перпендикулярную составляющую скорости не изменяя её величины. В данном случае сила Лоренца играет роль центростремительной силы, а происходящее под её действием движение в плоскости перпендикулярной к вектору индукции магнитного поля описывается уравнением равномерного движения по окружности со скоростью v_┴:.

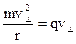B, (39.4)

откуда r – радиус кривизны траектории или радиус окружности равен:

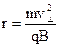. (40.4)

С учетом формулы (39.4) период обращения (Т) и угловая частота (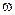) определятся из равенств:

, (41.4)

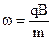. (42.4)

Сложение равномерного движения частицы вдоль направления магнитного поля со скоростью v_║ с равномерным вращением по окружности приводит в результате к траектории движения частицы по винтовой линии. Шаг винтовой линии равен расстоянию, на которое переместится частица в направлении поля за время полного оборота:

l=v_║Т= 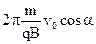, (43.4)

где 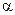-угол между направлениями векторов начальной скорости частицы и вектора магнитной индукции (рис.19.4). Направление вращения составляет левовинтовую систему с вектором В для положительного заряда и правовинтовую систему для отрицательного заряда. Если в магнитном поле движется электрон, то с учетом численных констант входящих в уравнение (42.4) получим:

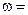1,7×10⁷В рад/сек. (44.4)

В уравнения (41.4 и 42.4) скорость частицы в явном виде не входит. Окружность, по которой движется заряженная частица (уравнение 40.4) под действием силы Лоренца принято называть ларморовой окружностью, а величину 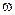- ларморовой частотой, по имени английского физика Лармора, изучавшего движение заряженных частиц в магнитных полях.

Предположим, что электронный пучок с малой угловой расходимостью выходит из точки О под средним углом 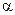, к вектору магнитной индукции В. Поскольку траектории электронов винтовые линии, то через интервал времени равный периоду обращения (см. уравнение 41.4) они пересекут силовую линию магнитного поля, проходящую через точку О₁ (рис.20.4). Расстояние, на которое они при этом продвинутся вдоль оси, т.е. шаг винтовой линии, определится по формуле (при условии что уго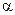л мал).

l=2 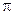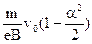(45.4)

Рис. 20.4. Фокусировка заряженных частиц

в продольном магнитном поле.

Таким образом, имеет место фокусировка электронного пучка проходящего под малым углом к силовой линии магнитного поля (параксиального пучка). При увеличении среднего угла ( 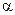) фокусировка ухудшается. Если в плоскости перпендикулярной к магнитному полю поместить объект, каждая точка которого испускает пучок с малой угловой расходимостью, то на расстоянии l сформируется изображение объекта с увеличением, равным единице. Следовательно, фокусирующее действие продольного магнитного поля может быть использовано для получения электронно оптического изображения.

В случае вхождения электронного пучка в магнитное поле, когда вектор скорости электронов перпендикулярен силовым линиям магнитного поля (вектору магнитной индукции В) при малой расходимости пучка (2f) пучок электронов вновь сфокусируется после поворота на угол 180⁰ (рис. 21.4). При этом ширина фокуса пучка (ВС) при радиусе (r) по которому движутся (электроны с заданной скоростью и в данном магнитном поле, при угле раствора пучка 2f, определится из равенства:

ВС=АС-АВ=2r-2r´cosf=4r´sin²(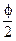), (46.4)

а, ширина фокуса (D=ВС) при малом угле определится по формуле:

ВС=D=rf². (47.4)

Таким образом, если рассматривать пучок электронов, вылетающих из точки А с угловой расходимостью в пределах (2f), то окажется, что около точки В этот пучок сходится в области определяемым равенством (47.4).

Поперечная магнитная фокусировка находит широкое применение в технике по разделению частиц по массе и заряду (масспектрометрия и разделение изотопов). Согласно формулам, (40.4 и 47.4) определяющий линейный размер области фокусировки в поперечных электромагнитных полях зависит от отношения массы частицы к её заряду. Поэтому частицы разного сорта (отличные по массе и заряду) будут фокусироваться в различных точках на участке ВС, и их можно улавливать соответствующими приемниками.

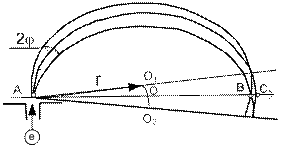
Рис.21.4. Фокусировка пучка заряженных частиц в

поперечном однородном магнитном поле.

Применительно к электронным пучкам ни продольная, ни поперечная фокусировки в однородном магнитном поле существенного практического значения не имеют. Наиболее важным оказывается только фокусировка электронных пучков с помощью коротких соленоидов. Такой соленоид создает аксиально-симметричное магнитное поле с отличными от нуля компонентами магнитной индукции. Фокусирующее действие аксиально-симметричного магнитного поля можно пояснить с помощью рис. 21.5, на котором в плоскости, проходящей через ось симметрии z, изображено сечение соленоида, четыре силовые линии магнитного поля - тонкий пунктир и две характерные траектории электронов - жирный пунктир. Электроны влетающие, в поле короткого соленоида, слева направо параллельно оси z показаны стрелками.

Качественно механизм фокусировки в коротком соленоиде (короткой магнитной линзе) можно разъяснить следующим образом. Пусть электроны влетают в поле короткой электромагнитной линзы со скоростью v, двигаясь слева направо (рис. 21.5). Для наглядности примем, что начальное вращение электрона отсутствует и его скорость направлена параллельно оси z. Тогда в первые моменты движения электрона в поле кроткого соленоида, на него будет действовать только сила от составляющей магнитного поля:

F_f=e(v_zB_r), (48.4)

которая вызовет вращение электрона по азимуту со скоростью v_f. Если B_r направлено, так как представлено на рис. 21.5, то в области z<0 в верхней части соленоида компонента скорости v_f направлена к читателю, а в нижней части,

Рис.22.4. Фокусировка электронных пучков

в короткой магнитной катушке.

напротив, - от него т.к. (e<0). Только после появления радиальной составляющей скорости v_f начнет сказываться фокусирующее действие короткого соленоида (магнитной линзы). В результате взаимодействия v_f и В_r возникнет движение в радиальном направлении. Составляющая вектора индукции B_r магнитного поля вызывает вращательное движение электрона по спирали с переменным радиусом относительно оси z. Радиальная составляющая силы всегда направлена к оси, т.е. действие поля всегда будет фокусирующим, независимо от направления силовых линий и направления начальной скорости электрона. На протяжении всей первой половины линзы знак азимутальной компоненты силы не меняется и вращательная скорость v_f будет непрерывно нарастать. Одновременно за счет увеличения v_f и B_z будет нарастать фокусирующая сила F_r. После перехода электрона во вторую половину линзы (z › 0) знак B_r и вращательная скорость начнет постепенно уменьшатся. Однако знак фокусирующей силы остается неизменным, потому что знаки v_f и B_z не изменяются. В результате прохождения электрона через линзу его траектория окажется повернутой на некоторый угол относительно исходной плоскости (r,z) и пересечет ось (z) в том или ином месте, один или даже несколько раз за счет действия фокусирующей силы.

Дата добавления: 2017-01-14