Длина волны характеристических линий и потенциал возбуждения К-серии ряда элементов. 3 страница

= , (15.4)

и с учетом (14.4) получим закон преломления электронных траекторий на границе скачкообразного изменения электростатического потенциала:

= , (16.4)

где углы a и b могут быть названы по аналогии с геометрической оптикой углом падения и углом преломления. Равенство (16.4) полностью совпадает с законом преломления Снелля для геометрической оптики, но здесь роль коэффициента преломления играет квадратный корень из значения потенциала в данной точке поля. Это позволяет считать, что пучок электронов, движущихся в электростатическом поле, ведет себя точно так же, как световой луч в преломляющей среде, если электронно-оптический показатель преломления, определяемый уравнением (16..4), равен оптическому показателю преломления в каждой точке пространства.

Из соотношения Снелля (16.4) видно, что оно применимо и к ионному пучку. В случае положительно заряженных частиц, но с тем, же соотношением потенциалов, поле будет направлено в противоположную сторону, но сила, действующая на частицу, будет действовать в том, же направлении. Под действием этой силы компонента скорости частицы, перпендикулярная поверхности раздела, изменится, а параллельная составляющая скорости останется неизменной.

Полученный результат легко обобщить наглядным, хотя и не строгим способом, на случай произвольного электростатического поля которое можно всегда изобразить с помощью эквипотенциальных поверхностей (рис. 2.4).

U₁   U₂ ≥U₁ U₃≥U₂   U₄≥U₃

Рис.2.4. Преломление электронной траектории на эквипотенциальных поверхностях. Частица движется в ускоряющем электрическом поле.

Если эти поверхности проведены достаточно близко друг к другу, то при рассмотрении движения заряженной частицы можно считать, что потенциал в пространстве между двумя соседними эквипотенциалями постоянен и все изменение потенциала происходит маленькими скачками на самих эквипотенциальных поверхностях. В таком случае траектория частицы аппроксимируется ломаной линией, причем изменение направления траектории на каждом изломе определяется законом преломления. В пределе ломаная линия превращается в плавную кривую, которая описывает траекторию частицы в данном поле. Как следует из метода построения, эта траектория совпадает по форме с траекторией светового луча, распространяющегося в среде с переменным коэффициентом преломления, значения которого в различных точках пропорциональны квадратным корням из потенциалов. Это чрезвычайно важное замечание, влечет за собой множество следствий:

1. Поскольку электростатическое поле изменяется непрерывно, то электронно-оптический показатель преломления n= является непрерывной функцией координат. Согласно уравнениям (15.4) и (16.4) скорость заряженной частицы тем больше чем больше n. В случае световых лучей ситуация противоположна.

2. В геометрической оптике показатель преломления прозрачных сред изменяется в узких пределах (у стекла n≈1,5., а у алмаза n≈2,5). Кроме того показатель преломления можно изменить, только заменив среду. В противоположность этому электронно-оптический показатель преломления вдоль траектории заряженной частицы может меняться в любых пределах за счет изменения потенциала. В этом отношении аналогия со световой оптикой отсутствует, так как оптические свойства стеклянных линз неизменны.

3. Траектория частицы, движущейся в электростатическом поле полностью, определяется относительными значениями потенциалов в различных точках пространства (если значения потенциала отсчитываются от той точки пространства, из которой частица начала двигаться с нулевой скоростью). При этом, на форму траектории не оказывают ни какого влияния величина заряда и масса частицы, так как относительные значения коэффициентов преломления не зависят от этих величин. Если две частицы, различающиеся по величине массы и заряда (при одинаковом знаке заряда), начинают свое движение с нулевой скоростью из некоторой точки в электрическом поле, то их траектории будут идентичны (хотя они и будут пройдены частицами за разные промежутки времени). В этом заключается так называемый закон подобия для движения заряженных частиц в электростатическом поле.

4. Если известен закон движения частицы , где r расстояние от оптической оси z, то уравнение траектории получается переходом от времени (t) к натуральному параметру l-расстоянию вдоль траектории от её начальной точки. Из равенства , взятого по модулю, следует связь между дифференциалами:

dt= 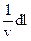. (17.4)

С учетом (17.4) уравнение (8.4) при переходе от переменной t к переменной l преобразуется к виду:

. (18.4)

Подставляя в (18.4) скорость, определяемую по уравнению (14.4), получим дифференциальное уравнение для траектории движения электрона 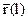в электростатическом поле:

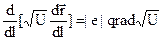. (19.4)

Данное уравнение является основным уравнением электронной оптики. Оно полностью аналогично уравнению светового луча в геометрической оптике, но в нем роль показателя преломления среды имеет функция - именуемая в специальной литературе электронно-оптическим показателем преломления.

3.4. Центрированные электронно-оптические системы.

Наиболее важное следствие введения электронно-оптического показателя преломления заключается в возможности непосредственного применения математического аппарата геометрической оптики к описанию движения пучков заряженных частиц в электрических полях. При этом, благодаря специфическим особенностям электростатического поля, возможности электронной оптики при конструировании центрированных оптических систем, во многих отношениях оказываются гораздо более широкими, чем возможности обычной оптики, в которой используется преломление световых лучей на границах прозрачных тел с коэффициентами преломления, изменяющимися в очень узких пределах.

Рис. 3.4. Схемы центрированных электронно-оптических систем и расположение эквипотенциальных поверхностей вблизи оптической оси.

В электронной оптике аналогом центрированной оптической системы служит электростатическое поле, обладающее аксиальной симметрией. Аксиально-симметричное электростатическое поле можно создать с помощью системы электродов, обладающих симметрией вращения (коаксиальных цилиндров, различным образом сопряженных центрированных диафрагм с круглыми отверстиями, колец) расположенных вдоль одной общей оси симметрии, играющей роль главной оптической оси. В практике электростатические линзы обычно собирают из простых электродов (комбинации апертур, колец и трубок рис. 3.4), которые легко изготовить. Единственными серьёзными проблемами при их сборке является необходимость учета электрического пробоя и накопления заряда на изолирующих поверхностях. В условиях рабочего вакуума электроды должны быть отделены друг от друга настолько, чтобы максимальная напряженность поля в зазоре не превышала 15кВ/м.

Изображенные на рис.3.4 эквипотенциальные поверхности соответствуют поверхностям, где коэффициент преломления n = const. При положительном потенциале средней диафрагмы n имеет в середине максимум. Эта система действует примерно так, как если бы (n) было постоянно между двумя эквипотенциальными поверхностями, а насамих поверхностях менялось быскачком. Таким образом, эквипотенциальные поверхности действуют как преломляющие поверхности в оптике, и, как видно из рисунка, внутренние поверхности, искривленные вовнутрь, должны действовать как рассеивающие, а внешние, искривленные наружу, как собирающие.

Действие электростатических линз можно объяснить на примере простой линзы, состоящей из двух цилиндров (рис. 3.4,в). Эквипотенциальные поверхности электростатического поля в зазоре между электродами вблизи оси z образуют линзу, как бы склеенную из бесконечно большого числа тонких менисков с постепенно изменяющимся коэффициентами преломления. Следовательно, пучок электронов (движущийся на небольшом расстоянии от оси z и под малыми углами к ней), будет вести себя подобно пучку световых лучей распространяющихся в оптически неоднородной среде. Выделим одну траекторию пучка (рис. 3.4,в). Силу К, действующую на электрон в каждой точке его пути можно разложить на две составляющие: параллельную оптической оси z и перпендикулярную к ней. На участке траектории до середины зазора радиальная составляющая силы направлена к оси z. Под действием этой силы траектория электрона будет постепенно приближаться к оси z. После прохождения через середину зазора электрон окажется под действием радиальной силы, стремящейся отклонить его от оси z. Следовательно, при условии U₁≤U₂ электроны ускоряются и должны фокусироваться слева и дефокусироваться справа от середины зазора. Однако фокусирующее действие радиальной составляющей силы, в зазоре, на первой половине пути не может быть скомпенсировано дефокусирующим действием на протяжении второй половины пути. Отсутствие компенсации обусловлено тем, что первую часть пути электрон движется с меньшей скоростью и, следовательно, дольше находится под действием силы, прижимающей его к оси z. В результате электронная траектория пересекает ось в точке F₂, расположенной справа от центра зазора. Эта точка является главным фокусом линзы образованной двумя цилиндрами.

При движении электронов справа налево, то есть со стороны цилиндра с U₂≥U₁ электронная траектория пересечет ось z в точке F₁, которая является вторым фокусом электростатической линзы. Таким образом, различие в величине потенциалов а, следовательно, и в величине оптических коэффициентов преломления, приводит к тому, что главные фокусные расстояния оказываются различными. Этот результат является типичным для многих электронно-оптических систем, а в геометрической оптике ему соответствует случай иммерсионной линзы. Если относительно центра зазора потенциал одинаков с обеих сторон линза называется не иммерсионной. Не иммерсионную линзу можно изготовить при центрировании трех цилиндров (либо трех диафрагм) крайние из которых находятся под одинаковом потенциале.

Формула тонкой электростатической линзы аналогична для таковой в геометрической оптике:

dz. (20.4)

Если а = ¥, т. е. на линзу падает параллельный пучок электронов, то величина b по определению равна главному фокусному расстоянию; а оптическая сила электростатической линзы определится как:

, (21.4)

Правило знаков для фокусного расстояния, как и в геометрической оптике: положительные значения f отвечают собирательным линзам, отрицательные рассеивающим.

Если линза иммерсионная, т. е. потенциал с обеих сторон разный, то расчет приводит к формуле:

, (22.4)

где f₁ и f₂ – соответственно переднее и заднее главные фокусные расстояния

определяемые из равенств:

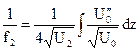, . (23.4)

Анализ полученных соотношений позволяет сделать следующее заключение:

1. Характерной отличительной особенностью электростатической линзы в нерелятивистском случае является независимость её фокусирующих свойств от отношения заряда частицы к её массе. Следовательно, если в системе будут использоваться ионы различных типов, то необходимо применять электростатические линзы, это свойство является следствием закона подобия отмеченного ранее.

2. На фокусирующие свойства линзы оказывает влияние только отношение потенциалов, и если необходимо совместить траектории частиц противоположных знаков, то достаточно просто поменять знаки всех потенциалов (включая и U₀). Следовательно, при расчетах линз можно ограничиться только вычислениями для электронов (т. е. для потенциалов положительно заряженных электродов) и надлежащим образом учитывать, что для положительных ионов потенциалы электродов будут иметь ту же абсолютную величину, но противоположный знак.

3. Специфическим свойством электростатических линз является то, что они не только фокусируют, но, кроме того, ускоряют либо замедляют частицы. Исключение составляют только одиночные линзы, в которых фокусировка происходит без изменения энергии частиц. Ускоряющие свойства электростатических линз используются в электронных и ионных источниках. Кроме того, электростатические линзы могут быть использованы для анализа и разделения частиц по энергиям (линзовые фильтры).

4.4. Фокусировка электронных пучков в аксиально-симметричных

электростатических полях.

1.4.4. Катодная линза.

Диафрагма с круглым отверстием (рис. 3.4,б) является простейшим элементом для получения электронного пучка, если плоский электрод, создающий электрическое поле слева от отверстия будет источником электронов, т.е. является катодом. Электроны, покидающие поверхность катода, ускоряются разностью потенциалов между диафрагмой (анодом) и катодом. При таком расположении электродов, и потенциалов как следует из уравнения (23.4), оптическая сила отрицательна, т. е. такая линза всегда дает расходящийся пучок электронов.

Ситуация может быть кардинально улучшена, если поместить вблизи катода еще одну диафрагму (электрод Венельта) и подать на незначительное отрицательное напряжение U_v ≤ -U₀/100по отношению к катоду (рис. 4.4,а). Этот контрольный электрод служит двум целям.

Рис. 4.4. Схема катодной линзы (а), формирование кроссовера (б).

Во-первых, он изменяет распределение поля таким образом, что создается фокусирующее поле вблизи поверхности катода, где электроны движутся относительно медленно. Следовательно, это фокусирующее влияние будет сильнее, чем дефокусирующее от отверстия анода. В результате будет формироваться сходящийся пучок. Во-вторых, меняя напряжение U_c, можно контролировать ток пучка. Электроны, покидающие поверхность катода, имеют максвелловское распределение скоростей. Наиболее вероятная энергия электронов пропорциональна температуре катода, и при Т=2700 К она приблизительно равна 0,2 эВ. Поэтому если U_c≈0,2 В (напряжение отсечки), то вблизи оптической оси потенциал на эквипотенциальных поверхностях меньше ≤0,2 В, и доля электронов, проникающих туда, будет очень мала, а, следовательно ток пучка практически будет нулевым. Если теперь слегка повысить потенциал на контрольном электроде, то все больше электронов будет проходить через область его влияния, и ток пучка резко возрастет вместе с радиальным расширением той части поверхности катода, из которой электроны могут его покинуть.

Так как разные электроны могут покидать одну и ту же точку поверхности катода во всевозможных направлениях, их траектории будут различны, и они пересекут ось в разных точках (рис. 4.4,б). В результате изображение поверхности катода будет сформировано в виде кроссовера, положение которого определяется тем, где большинство электронов пересекут ось (рис.4.4,б). Поперечное сечение кроссовера намного меньше, чем катода, но вследствие упомянутого распределения начальных скоростей оно никогда не может быть сведено к нулю. Диаметр кроссовера зависит от геометрии деталей линзы и приложенной разности потенциалов и обычно изменяется в пределах от 20 до 100 мкм.

Само существование кроссовера зависит от положения вершины катода по отношению к контрольному электроду: он существует только тогда, когда катод расположен на достаточном удалении позади контрольного электрода. Максимальная передача тока в линзе около 0,2%, большая часть тока теряется на электродах.

В большинстве электронных линз кроссовер формируется на небольшом удалении от катода. Однако можно сконструировать линзы, формирующие кроссовер и на большом расстоянии от катода (телефокусные линзы). Они обеспечивают более высокую передачу тока за счет увеличения размеров кроссовера.

Рассмотренную линзу называют катодной линзой либо электростатическим «иммерсионным» объективом по аналогии с соответствующим оптическим объективом, где показатель преломления в пространстве предметов отличается от показателя преломления в пространстве изображений. Такая катодная линза является одним из основных элементов термоэлектронного эмиссионного микроскопа.

2.4.4. Электронные пушки.

Совокупность электродов, формирующих электронный луч, называют электронной пушкой. Термин «Электронная пушка» применяют как к устройствам для формирования высокоинтенсивных электронных пучков (сильноточные электронные пушки), так и простым совокупностям электродов для получения пучков малой интенсивности (слаботочные электронные пушки) обычно используемые в телевизионных системах, электронных микроскопах, осциллографах, электронно оптических преобразователях и др. приборах. По конструкции и параметрам электродов слаботочные электронные пушки весьма разнообразны, но работают по одному принципу. В качестве примера рассмотрим работу слаботочной трехэлектродной пушки стандартной конструкции.

Различие между катодной линзой и электронной пушкой состоит только в том, что при её конструировании не ставят целью воспроизвести изображение структуры поверхности катода, а добиваются прохождения как можно большего тока, как можно, через меньший кроссовер. Поэтому цель конструирования любой пушки это совместить большую яркость и низкий разброс энергий. Это является следствием закона Гельмгольца - Лагранжа из которого следует что «яркость пучка р», определяемая как отношение плотности тока в фокусе к телесному углу, в пределах которого распространяется сфокусированный пучок, не зависит ни от числа линз в системе, ни от их оптической силы. Теоретический предел яркости определяется из равенства:

_{, (24.4)}

где U₀ – ускоряющее напряжение. Для типичных значений i=1 А/cм², Т=2460 К и U₀=20 кВ предельная яркость равна 2,8 ×10⁴ А/(cм²ср).

Теоретическую яркость не всегда удается получить на практике, хотя к ней можно приблизиться подбором материала эмиттеров и соответствующих рабочих условий.

а б

Рис. 5.4. Схема устройства и питания слаботочной трёхэлектродной пушки. а) с автоматическим смещением; б) с управляемым смещением.

В трехэлектродных (триодных) низкоточных термоэмиссионных пушках в качестве материала нити обычно используют вольфрамовую проволоку, диаметром ≤ 0,125 мм, в форме буквы V, нагреваемую током до температуры около ≈2700 К.

Нить накала (рис. 5.4) как правило, сменная и при её установке необходима строгая центровка по отношению к отверстию в электроде Венельта, иначе ось электронного пучка составит некоторый угол с оптической осью системы. Качество работы пушки во многом зависит от расстояния острия нити до электрода Венельта. Удаление нити от анода вдоль оси пушки приводит к уменьшению тока пучка и делает ток менее чувствительным к боковым смещениям нити. Поэтому положение острия нити выбирают в зависимости от того, что более важно в конкретных условиях — величина тока или его стабильность. Оптимальное расстояние электрода Венельта от анода зависит от ускоряющего напряжения и, не должно превышать минимального расстояния, при котором еще можно избежать электрического пробоя. Для удовлетворения этим условиям при разных ускоряющих напряжениях, в конструкции электронных микроскопов предусмотрены выведенные наружу приспособления для юстировки: в частности, перемещение пушки как целого относительно анода или поперечное движение самого анода позволяющие центрировать нить по максимуму тока электронного пучка в работающей установке.

Нить накала нагревают постоянным, либо переменным (с частотой 100кГц) током. Величина тока накала стандартной вольфрамовой нити составляет ≤ 3 А. Источник накала изолирован от земли и имеет средний вывод для того, чтобы потенциал острия нити не изменялся, при изменении тока накала. В режиме насыщения эмиссия пушки мало чувствительна к небольшим колебаниям температуры, поэтому высокая стабилизация тока накала не требуется.

Срок службы вольфрамовой нити ограничен вследствие распыления вольфрама из наиболее горячего участка нити вблизи острия. Если внутреннее сопротивление источника тока накала велико (случай источника постоянного тока) то уменьшение толщины нити ведет к увеличению её температуры и сокращению времени работы. Наоборот, при работе с источником постоянного напряжения (с низким внутренним сопротивлением) температура нити падает. Изменение температуры нити, вызванное распылением вольфрама, можно уменьшить, используя источник питания с внутренним сопротивлением, примерно втрое большим, чем сопротивление нити (обычно 1 Ом).

Рабочие характеристики катода из гексаборида лантана намного ниже, поэтому он может работать при более низких температурах (1900 К), что удлиняет его время жизни (сотни или даже тысячи часов). Такие катоды могут обеспечить плотность тока эмиссии на порядок выше, чем нитевидные вольфрамовые катоды, а их яркость может достигать ≤ 1,6×10⁵ А/ (см².ст). Они имеют косвенный подогрев, а радиус их вершины очень мал (1—10 мкм). Разброс энергии всего лишь около 1 эВ. Единственным их недостатком является высокая химическая активность при повышенных температурах и неоднородное распределение яркости.

Самый простой способ подачи необходимого отрицательного напряжения на электрод Венельта (напряжения смещения) состоит в пропускании тока пушки через сопротивление порядка нескольких мегом (рис. 5.4,а). Такое смещение, называемое «автоматическим» стабилизирует ток пушки из-за отрицательной обратной связи. При увеличении эмиссии напряжение смещения возрастает, что приводит к уменьшению тока пушки. Термоэмиссия с нити вначале быстро увеличивается с ростом температуры, но затем, при наличии смещения достигает «насыщения», соответствующего определенной температуре накала (рис. 6.4). Стабильность пушки в режиме насыщения значительно выше, чем в иных условиях. «Плато» (рис. 6.4,б) почти горизонтально при достаточно большом сопротивлении смещения.

а б

Рис.6.4. Зависимость плотности тока эмиссии с вольфрамовой нити от температуры (а) и тока эмиссии пушки от температуры нити при различном напряжении смещения (б).

На (рис. 5.4,б) представлена схема, которая обеспечивает большую эффективную величину сопротивления смещения, особенно при низких напряжениях смещения. Постоянное сопротивление в этой схеме заменено триодом с большим сопротивлением смещения в катоде, благодаря которому триод практически рабо -

а б

Рис.7.4. Зависимость тока эмиссии пушки и тока пучка (зонда) от температуры накала (а). Зависимость яркости пучка от величины напряжения смещения и расстояния (h) нить – электрод Венельта (б).

тает в пентодном режиме.

Эффективное сопротивление триода равно (a+1)R; где a – коэффициент усиления триода; R – сопротивление в катоде. Для типичных величин a=100 (триод 12АХ7) и R=660 кОм эквивалентное сопротивление триода равно 67 Мом, т. е. намного превышает величину сопротивления, обычно используемую в цепи автоматического смещения. В результате достигается лучшая стабильность тока пушки.

Ток эмиссии с единицы площади катода быстро возрастает с температурой (рис. 7.4,а), но столь, же быстро увеличивается и скорость распыления вольфрама.

Экспериментально установлено, что время работы нити толщиной 0,125 мм (в часах) и плотность тока i (А/cм²) связаны простой зависимостью t=50/i. Из неё следует, что плотность тока в 1 А/см², получаемая при температуре 2640 К, - это наивысшая возможная плотность тока, совместимая с разумным сроком работы нити (около 50 часов). Величина яркости достигает максимума при смещении, примерно на 50 В меньше величины, при которой происходит запирание пушки (рис.7.4,б). Характер зависимости величины запирающего смещения от расстояния нить – электрод Венельта (рис.7.4,б) можно понять, анализируя электростатическое поле вблизи острия нити. Электроны могут покинуть нить только в том случае, если эквипотенциальные поверхности, соответствующие потенциалу нити (-U₀, U_v), пересекают остриё нити, в противном случае пушка оказывается запертой.

При большом расстоянии (h) от сетки (электрода Венельта) до острия нити пушка запирается малым напряжением смещения U_в, и по мере уменьшения (h) необходимо увеличивать U_в, чтобы сохранить постоянство условий вблизи острия. Аналогичная ситуация возникает при увеличении диаметра отверстия в электроде Венельта, когда для сохранения приблизительного постоянства рабочих условий приходится также увеличивать величину h.

Хорошая стабильность по току пучка пушки возможна только при работе в режиме насыщения. Ток пучка достигает насыщения при более высокой температуре накала, чем ток пушки (рис. 7.4,а). Поэтому рабочая температура нити должна соответствовать началу горизонтального участка кривой зависимости тока зонда от температуры и быть близка к и 2640 К для того, чтобы обеспечить высокую яркость пучка и достаточный срок службы.

3.4.4. Автоэмиссионные пушки.

Электронные слаботочные пушки с автоэмиссионным катодом (рис. 8.4) по яркости в 10³ раз превосходят яркость обычной трехэлектродной пушки стандартной конструкции, а эффективный диаметр источника электронов соответствует ≈3нм. Катод представляет собой острие из вольфрама диаметром 0,2 мкм. В пушке два анода с разными ускоряющими потенциалами: один управляет полем вблизи острия, другой ускоряет электроны. Фокус диаметром около 25 нм расположен за вторым анодом; линза уменьшает диаметр пучка до 1нм и менее.

Автоэмиссионная пушка для электронных микроскопов превосходит обычную пушку лишь в том случае, если диаметр электронного пучка менее 0,1 мкм. Наиболее важной областью применения автоэмиссионных пушек является просвечивающая электронная микроскопия и микрозондовый анализ. В этом случае применение пушек с высокой яркостью пучка наиболее эффективно.

Рис.8.4. Схема электронной пушки с автоэмиссионным катодом.

4.4.4. Электронный прожектор.

В триодных пушках изменение напряжения на электроде Венельта необходимо не только для фокусировки пучка, но и для контроля его тока одновременно. Поэтому трудно поддерживать постоянное положение и размеры кроссовера при изменении тока пучка. Эту трудность можно преодолеть, увеличив число электродов (рис.9.4).

Дата добавления: 2017-01-14