Метод наименьших квадратов

КОСВЕННЫЕ ИЗМЕРЕНИЯ.

Пусть требуется измерить величину q=q (x 1,x 2,…,xn), где x1,x 2,…,xn определяют прямыми измерениями.

1.Для каждой.величины x1 произвести расчеты по процедуре, описанной в &5.1 и записать результаты в виде:

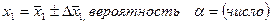(15.2.1)

2.Вычислить среднее значение функций

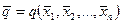(15.2.2)

3.Вычислить доверительный интервал для величины , соответствующий вероятности

a=68% по формуле:

(15.2.3)

Если, например, величина

-точные числа), то доверительный интервал, как следует из (5.2.3), удобно вычислять по формуле:

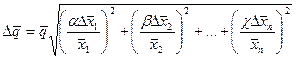(15.2.4)

4. Окончательный результат записать в виде: q = ğ ± Δğ, вероятность a=(число) (15.2.5).

5. При необходимости доверительный интервал можно рассчитать -для большей вероятности.

При выполнении эксперимента часто измеряют две величины х и у, причем у является функцией х. Найденное значения откладывают на графике и"пытаются. построить кривую, которая наилучшим образом отражает зависимость y=f(x). Ограничимся случаем линейной зависимости

у =bx + a (16.1)

Задача состоит в том, чтобы найти параметры b и а, при которых прямая, выражающая на графике. зависимость (16.1), наилучшим образом проходила бы через экспериментальные точки.

Пусть величины х и у измеряются прямым способом,ихслучайные погрешности распределены по нормальному закону, а систематическими погрешностями можно пренебречь.

Представим все экспериментальные данные Х1 и Y1.на графике. Геометрически задача измерения a и b состоит в определении параметров некоторой прямой: значения ординаты при нулевом значении.абсциссы и тангенса угла наклона соответственно.

Рис.9

По имеющимся очкам на графике можно провести не единственную прямую. Однако, в теория доказывается, что наилучшей

прямой такая, для которой сумма квадратов разностей

(16.2)

будет минимальна, то есть

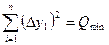(16.3)

Это условие выполняется, если производные будут равны нулю:

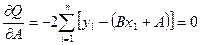(16.4)

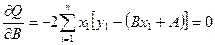(16.5)

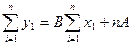(16.6)

Отсюда находим:

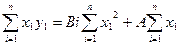(16.7)

Из (16.6) и (16.7) следует, что наилучшей оценкой В является следующее выражение:

(16.8)

а оценкой А: (16.9)

где 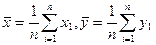(16.10)

Используя (16.10) формулу (16.8) можно преобразовать к виду:

(16.11)

Для определения погрешностей бывает достаточно вычислить стандартное отклонение коэффициента В или интервал, в котором с установленной' вероятностью может находиться коэффициент b. Стандартное отклонение коэффициента В определяется по формуле:

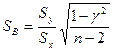, (16.12)

в которой

, (16.13)

, (16.14)

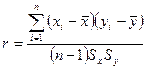, (16.15)

Интервал, в котором с задаваемой вероятностью a может находиться коэффициент В, записывается в виде:

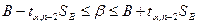, (16.16)

где В определяется формулой (16.11); Sв - формулой (16.12);.ta,n-2 - коэффициент Стьюдента для надежности a и значения параметре n-2; n - число пар экспериментальных точек.

Стандартное отклонение коэффициента А определяется по формуле:

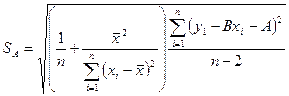, (16.17)

Рассмотрим следующий пример. Пусть произведено десять измерений пар величин х и у. Цифровые значения х могут быть фиксированными, то есть абсолютно точными. Необходимо: определить коэффициенты a и b (см.(16.1)).

Таблица 7

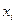
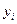
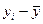
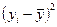
0,2	-0.9	0,81	0,31	-1,36	1,85	1,22
0,4	-0,7	0,49	0,59	-1,08	1,17	0.76
0.6	-0,5	0.25	0,82	-0,85	0.72	0,42
0.8	-0,3	0.09	1,17	-0.50	0,25	0,15
1,0	-0.1	0,01	1.66	-0,12	0.01-	0,01
1.2	0,1	0,01	1.87	0,20	0,04	0,02.
1.4	0,3	0,09	2,20	0,53	0.28	0,16
1,6	0.5	0,25	2,35	0,68	0,46	0.34
1.8	0,7	0,49	2,65	0.98	0,96.	0,69
2,0	0,9	0.81	3,20	1.53	0,44	1,38

По формулам (16.10) находим:

=1,1; =1,67.

По формулам (16.9) и (16.11) определяютА и В:

А=-0,02, В=1,54.

Уравнение для наилучшей прямой имеет вид:

У=1,54х-0,02.

Оценка стандартного отклонения для коэффициента В рассчитываем по формуле (16.12):

S в =0.11.

Интервал, в котором с вероятностью a =0,90 находится коэффициент b, имеет вид:

1,54 ±0,21, вероятность a =0,90

При • вычислении интервала использована величина ta<n-2=1,9 (см. Таблицу 1. Приложения).

Дата добавления: 2015-07-13