Определение параметров и формирование производственной функции

Пример выполнения работы

Динамические ряды по основному капиталу, численности рабочих и ВВП за 20-летний период деятельности хозяйственной системы приведены в табл. 2.2.

Т а б л и ц а 2.2

Годы	Капитал	Труд	ВВП

Постоянные параметры, характеризующие норму накопления, равны и соответственно.

Данные из табл. 2.2 поместим на лист Excel в блок ячеек A2: D21, как показано в табл. 2.3.

Т а б л и ц а 2.3

	A	B	C	D	E	F	G	H	I	J
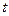
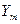
							6,5073	7,8228		8,9034
							6,5206	7,8240		8,9285
							6,5309	7,8268		8,9505
							6,5425	7,8300		8,9747
							6,5525	7,8320		8,9971
							6,5653	7,8356		9,0218
							6,5723	7,8368		9,0414
							6,5723	7,8376		9,0568
							6,5848	7,8411		9,0814
							6,5958	7,8427		9,1037
							6,6039	7,8454		9,1250
							6,6053	7,8489		9,1411
							6,6067	7,8521		9,1572
							6,6161	7,8555		9,1796
							6,6161	7,8567		9,1948
							6,6201	7,8602		9,2131
							6,6307	7,8629		9,2356
							6,6386	7,8633		9,2559
							6,6503	7,8652		9,2794
							6,6554	7,8652		9,2977

Производственную функцию Кобба-Дугласа с учетом технического прогресса (модель Солоу) будем искать в виде уравнения

с неизвестными параметрами , , 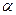, 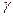. Логарифмируя эту функцию, получим

. (2.11)

Из равенства (2.11) следует, что значения функции линейно зависят от значени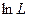й , и 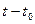. Поэтому коэффициенты 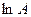, , 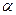и 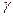уравнения (2.11) можно определить в Excel с помощью процедуры =ЛИНЕЙН().

Колонки E и F табл. 2.3 временно оставим пустыми. Дополним табл. 2.3 колонками G, H, I, J, в которые поместим значения величин , , 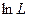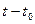и , входящих в соотношение (2.11). Для применения процедуры =ЛИНЕЙН()на свободном месте листа Excel выделим блок ячеек из одной строки и 4 столбцов. Затем в списке функций находим процедуру = ЛИНЕЙН(). На экране появляется окно, в поля которого надо ввести 4 аргумента:

· одномерный массив значений результирующего фактора (отклика) ;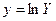

· двумерный массив значений факторов , , ;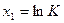

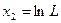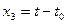· значение ИСТИНА (или число 1), так как в уравнении присутствует свободный член;

· значение ЛОЖЬ (или число 0), поскольку требуется вычислить лишь коэффициенты уравнения регрессии.

Одновременное нажатие трех клавиш “Ctrl”+”Shift”+”Enter” приводит к появлению коэффициентов уравнения (2.11) в ячейках выделенного блока.

Выделим, например, блок ячеек G23: J23 и запишем функцию =ЛИНЕЙН с необходимыми аргументами. Тогда для исходных данных табл. 2.3 в командной строке будет находиться выражение

{=ЛИНЕЙН(J2: J21; G2: I21; 1; 0)},

а результаты расчетов отображаются в виде табл. 2.4.

Т а б л и ц а 2.4

	G	H	I	J
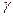
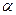
	0,0145	0,2400	0,7385	2,2205
				9,2120

В блоке ячеек G23: J23 содержатся коэффициенты уравнения линейной зависимости (2.11) в обратном порядке:

, , , .

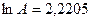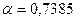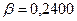В ячейке J24 вычислим параметр в соответствии с формулой

= EXP(J23).

Тогда получим 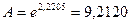. Само уравнение производственной функции имеет вид

. (2.12)

При отсутствии технического прогресса получим следующее уравнение производственной функции

. (2.13)

Дата добавления: 2015-07-13