I.4. Доказательство конфигураций пентоз и гексоз D-ряда

D-аллоза D-альтроза D-глюкоза D-манноза D-гулоза D-идоза D-галактоза D-талоза

Как уже отмечалось, к простейшим моносахаридам относятся также и кетозы. Те из них, которые встречаются в природе, всегда содержат кетонную группу во втором положении:

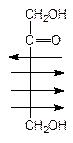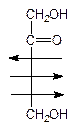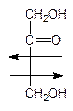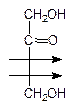Рибулоза Ксилулоза Фруктоза Седогептулоза

Конфигурации при каждом асимметрическом атоме в их молекулах могут быть доказаны с помощью реакции эпимеризации и получением озазонов, а также окислением до сахарных кислот.

Приведенный выше вывод возможных структурных формул альдоз D-ряда был сделан Фишером сначала только теоретически. Из разнообразных природных объектов выделено большое число альдоз D-ряда. Было необходимо доказать, что данная альдоза имеет такую-то из приведенных выше конфигураций. Чтобы решить эту задачу, необходимо познакомиться с некоторыми реакциями альдоз. Одной из таких реакций является окисление их концентрированной азотной кислотой, при котором до карбоксильной группы окисляется как карбонильная, так и первичноспиртовая группы. Из эритрозы при этом получается оптически недеятельная мезовинная кислота, а из треозы - оптически активная винная.

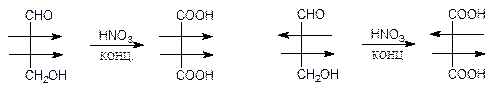Эритроза Мезовинная Треоза Винная

кислота кислота

Эта реакция, которая сразу позволяет определить, какую конфигурацию имеет данная тетроза, называется «уравниванием концов». Аналогичное уравнивание концов может быть также осуществлено восстановлением альдоз до полиолов боргидридом натрия.

Важное значение для структурных исследований (и синтетических целей тоже) имеют реакции удлинения и укорочения углеродной цепи альдоз. Рассмотрим важнейшие из них.

Углеродная цепь альдозы может быть удлинена на один атом углерода с помощью циангидринного синтеза. Дальнейшее превращение цианогруппы в альдегидную, т.е. переход от циангидрина к соответствующей альдозе, осуществляют чаще всего одним из двух методов.

Первый включает гидролиз циангидрина до соответствующей оксикислоты и восстановление образующегося из нее лактона амальгамой натрия в воде. Второй метод основан на прямом восстановлении циангидрина водородом в присутствии палладия в среде водного аммиака.

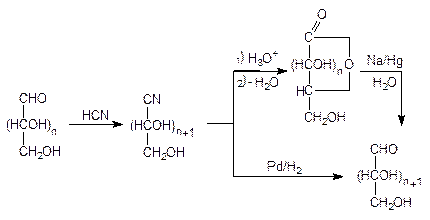
Имеется два наиболее распространенного способа укорочения цепи альдоз.

Первый из них основан на последовательном окислении альдегидной группы в карбоксильную и a-гидроксильной группы в кетонную с дальнейшим декарбоксилированием полученной a-кетонокислоты.

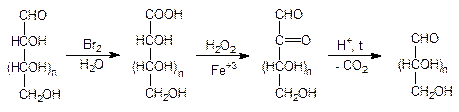Согласно второму методу из альдозы сначала получают оксим. Последний затем обрабатывают уксусным ангидридом; при этом оксимная группировка переходит с потерей воды в нитрильную (что характерно для оксимов альдегидов) и все гидроксильные группы ацетилируются. Полученное производное обрабатывают аммиачным раствором оксида серебра. Реакция сопровождается отщеплением (в результате гидролиза) ацетильных групп и расщеплением полученного циангидрина под действием основания (обратимость циангидринного синтеза). Отщепляющийся цианистый водород связывается оксидом серебра. Получается альдоза, содержащая на один атом углерода меньше, чем исходная.

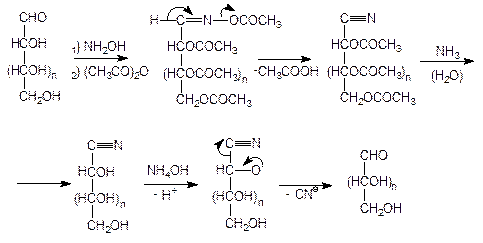
Используя описанные выше реакции, можно, как показал Э.Фишер, доказать конфигурацию любых альдоз. Рассмотрим, как это можно сделать для всех пентоз D-ряда и любой из D-гексоз.

Если произвести “уравнивание концов” всех пентоз D-ряда, то мы получим мезоформы соответствующих двухосновных кислот, которые оптически недеятельны в случае рибозы и ксилозы, и обладают оптической активностью в случае арабинозы и ликсозы.

Если мы подвергнем те же пентозы последовательно укорочению цепи и уравниванию концов, то из рибозы и арабинозы получим оптически недеятельную мезовинную кислоту, а из ксилозы и ликсозы - оптически активную винную кислоту.

В таблице 1 представлена зависимость оптической активности получаемых двухосновных кислот от строения исходных пентоз и использованных реакций («+» - кислота оптически активная; «-» - кислота оптически неактивная).

Приведенная таблица показывает, что описанный подход позволяет однозначно установить конфигурацию любой пентозы.

Таблица 1

Пентоза	Операции
Уравнивание концов	Укорочение цепи + Уравнивание концов
Рибоза Арабиноза Ксилоза Ликсоза	- + - +	- - + +

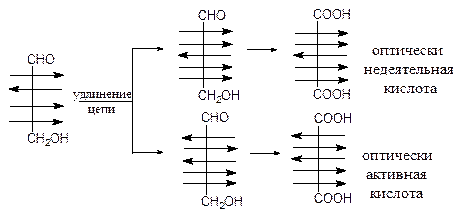Рассмотрим на примере глюкозы как установить конфигурацию той или иной гексозы. Если в результате укорочения цепи получена арабиноза, то исходным веществом могли быть глюкоза или манноза. Уравнивание концов в применении к рассматриваемому случаю не поможет сделать выбор между указанными гексозами, т.к. обе они при этом дают оптически активные кислоты. Чтобы ответить на вопрос о том, какая из гексоз глюкоза или манноза перед нами, необходимо прибегнуть к последовательному удлинению цепи и уравниванию концов исследуемой гексозы. При этом, как видно из приведенной ниже схемы, глюкоза даст одну оптически деятельную двухосновную кислоту и одну – оптически недеятельную, а манноза - две оптически деятельные.

Аналогичным образом можно различить гексозы гулозу и идозу. Например, из гулозы получаются две оптически деятельные кислоты, а из идозы - одна оптически деятельная и одна оптически недеятельная кислоты.

Рассмотренным выше операциям Фишер подверг все известные альдозы D- и L-рядов и установил, таким образом, строение каждой из них. Это позволило сделать пространственное отнесение известных альдоз, имевших лишь тривиальные названия.

Дата добавления: 2015-07-13