Построение эпюры материалов

Определение площади продольной арматуры, расположенной в подрезке

Вычислим изгибающий момент в нормальном сечении, расположенном в уменьшенной по высоте части ригеля:

(2.48)

где 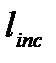- проекция наклонной трещины, развивающейся из угла подрезки.

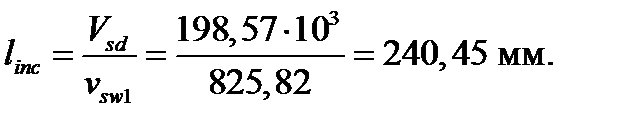(2.49)

Определим :

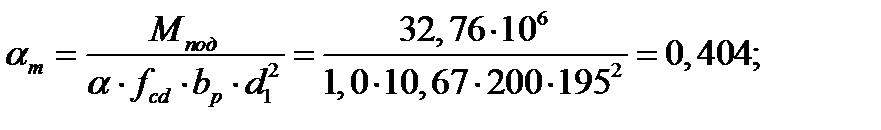(2.50)

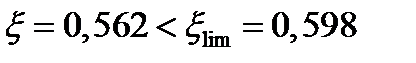, следовательно, растянутая арматура достигла предельных деформаций.

Требуемая площадь сечения растянутой арматуры в подрезке определяется по формуле:

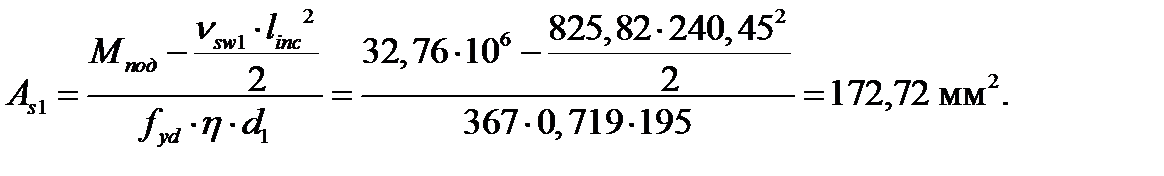
Принимаем 2 стержня Æ12 мм S400 с

Определим длину анкеровки продольной арматуры:

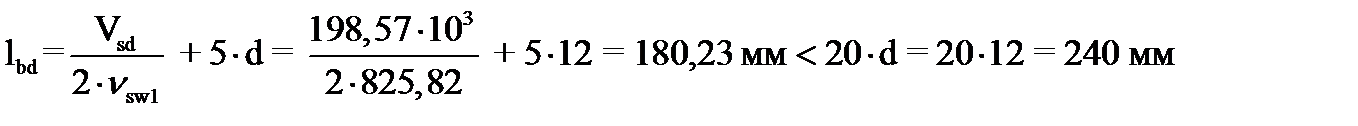, следовательно, принимаем

С целью экономичного армирования и обеспечения прочности сечений балки строим эпюру материалов, представляющую собой эпюру изгибающих моментов, которые может воспринять элемент по всей длине. Значение изгибающих моментов в каждом сечении при известной площади рабочей арматуры вычисляют:

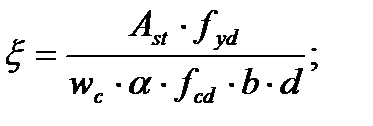
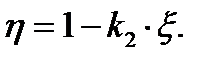(2.51)

На участках с значения 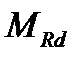постоянны и эпюра изображается прямой линией (см. графическую часть). При обрыве стержней с целью обеспечения прочности наклонных сечений по изгибающему моменту их заводят за сечение, где они не требуются по расчету на длину не менее .

Эпюра материалов должна охватывать эпюру изгибающих моментов.

Армируем пролёт 3-мя стержнями Æ32 мм S400. Один стержень Æ32 мм S400 обрываем в пролёте. Заводим на длину 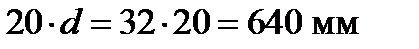от места их теоретического обрыва. 2 стержня Æ32 мм S400 доводим до обеих опор. Вычислим изгибающие моменты, воспринимаемые этими стержнями:

2Ø32:

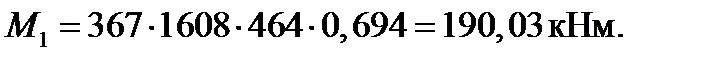
1Ø32:

>

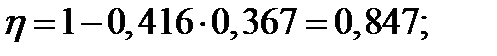
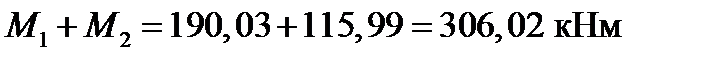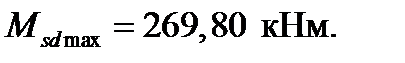
Так как в средних пролетах могут возникать значительные отрицательные моменты, для их восприятия по всей длине пролетов устанавливаются стержни 2 Æ12 S400.

Результаты расчетов сводим в таблицу 13.

Таблица 13 - Вычисление ординат эпюры материалов для продольной арматуры

⌀ и количество стержней	Уточненная высота сечения d = h - c, мм	Фактическая площадь сечения стержней, Ast, мм^2	Расчетное сопротивление арматуры, fyd, МПа	Относительная высота сжатой зоны, ξ	Коэффи-циент η	Момент MRd, кН∙м
Нижняя арматура в пролете (b=200мм)
2⌀32				0,736	0,694	190,03
1⌀32		804,2		0,367	0,847	115,99
Верхняя арматура в пролете
2⌀12				0,103	0,957	36,83
Нижняя арматура на опоре
2⌀12				0,246	0,898	14,52
Верхняя арматура на опоре
2⌀12				0,246	0,898	14,52

2Ø12:

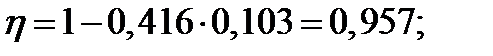
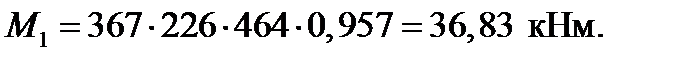
В подрезке

2Ø12:

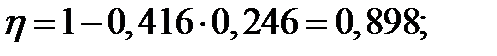
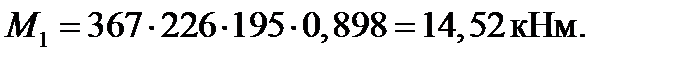
Список используемой литературы

1.СНБ 5.03.01-02 Бетонные и железобетонные конструкции.- Мн.,2003.

2.СНиП 2.03.01-84^* Бетонные и железобетонные конструкции.- М.,1985.

3.Железобетонные конструкции. Основы теории, расчёта и конструирования.

Под ред. проф. Т.М.Пецольда – Брест, БГТУ,2003.

4.СНиП 2.02.01-83. Основания зданий и сооружений. – М., 1984.

5. Пособие по проектированию бетонных и железобетонных конструкций из тяжёлых и лёгких бетонов без предварительного натяжения арматуры (к СНиП 2.03.01-84). М., 1986.

6. СНиП 2.01.07-85. Нагрузки и воздействия. Нормы проектирования. М., 1986.

7. Голышев А.Б., Бачинский В. и др. Проектирование железобетонных конструкций. К.,1985.

8. Кудзис А.П. Железобетонные и каменные конструкции. Часть 1,2. М., высшая школа, 1989.

9.Мандриков А.П. примеры расчёта железобетонных конструкций. Стройиздат 1989

10.ГОСТ 21.503-80. Конструкции бетонные и железобетонные (Рабочие чертежи).

Дата добавления: 2015-08-31