Алгоритм метода частичных потоков

Транспортная задача по критерию стоимости

Пример нахождения максимального потока

Дана транспортная сеть (рисунок 3.3). Найти для нее максимальный поток.

x₂ (9) x₃

3 4

(6) 2 (9)

x_{0 (}4) z

(7) (5)

4 x₁ (3) x₄ 3

Рисунок 3.3 – Транспортная сеть

Таблица 3.3 – Первый этап решения задачи

xi
	(0^+,¥)
	(0^+,3)
	(0^+,3)
	(2^+,3)
	(3^+,3)
	(3^+,3)

x₂ (9) x₃

6 7

(6) 2 (9)

x_{0 (}4) z

(7) (5)

4 x₁ (3) x₄ 3

Рисунок 3.4 – Транспортная сеть после первого этапа

Таблица 3.4 – Второй этап решения задачи

xi
	(0^+,¥)
	(0^+,3)
	---
	(1^+,2)
	(1^+,1)
	(4^+,1)

x₂ (9) x₃

7

2 (9)

x_{0 (}4) z

(7) (5)

5 x₁ (3) x₄ 4

Рисунок 3.5 – Транспортная сеть после второго этапа

Таблица 3.5 – Третий этап решения задачи

xi
	(0^+,¥)
	(0^+,2)
	---
	(1^+,2)
	(3^+,2)
	(3^+,2)

x₂ (9) x₃

9

4 (9)

x_{0 (}4) z

(7) (5)

7 x₁ x₄ 4

Рисунок 3.6 – Транспортная сеть после третьего этапа

Максимальный поток: 3+1+2=6.

Известно, что стоимость перевозки по дуге единицы груза .

Требуется определить 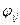- количество груза, который нужно перевести из 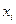в 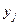, чтобы обеспечить общую минимальную стоимость перевозки.

Задача решается исходя из теории потоков.

Введём обозначения:

- пропускная способность дуги из 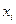в ;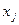

- стоимость прохождения единицы потока по дуге ;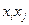

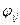- поток, проходящий по дуге .

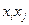Стоимость всего пути по дуге : .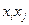

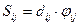Считают, что задана транспортная сеть с наибольшим потоком 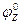. Требуется пропустить по данной сети поток, не превышающий 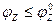таким образом, чтобы общая стоимость прохождения потока была наименьшей, т.е. обеспечивался минимум:

где 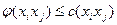, поток по дуге не должен превышать пропускную способность.

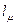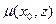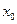Считаем, что - длина пути, тогда стоимость прохождения некоторого потока по пути из в 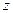равна: .

Существует два варианта решения транспортной задачи:

1 вариант. На пропускную способность дуг не накладывается никаких ограничений. Тогда задача решается простым нахождением кратчайшего пути.

2 вариант. На пропускную способность дуг накладываются ограничения. В этом случае задача решается методом частичных потоков.

1. В простейшем графе 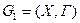ищем кратчайший путь из 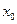в , .

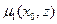2. Пусть в результате пункта 1 определили путь , имеющий пропускную способность 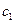, т.е. .

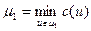3. Пропускаем по данному пути поток , так что

4. Производим замену пропускной способности дуг по правилу:

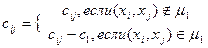
5. Поток, который необходимо пропустить по транспортной сети, уменьшаем на , .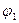

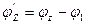6. Исключаем из дальнейшего рассмотрения дуги, у которых .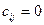

7. Рассматриваем новый граф , как частичный граф исходного и переходим к пункту 1 для пропуска по транспортной сети потока .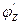

Данные потоки 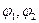и т.д., полученные на определённых шагах итерации называются частичными потоками.

8. Алгоритм останавливается, когда , .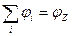

Общая стоимость перевозки определяется по формуле (1).

Решение данной задачи основано на определении кратчайшего пути в графе, который определяется для каждого частичного графа, в частности по алгоритму Дейкстры.

Дата добавления: 2015-08-31