Алгоритм Краскала нахождения остова минимального веса

Задача об остове минимального веса (о кратчайшем остове):

в связном взвешенном графе порядка 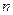найти остов минимального веса.

Алгоритм Краскала, решающий эту задачу, заключа­ется в следующем.

1. Строим граф 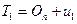, присоединяя к пустому графу на множестве вершин 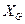ребро 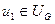минималь­ного веса.

2. Если граф уже построен и , то строим граф , где - ребро графа G, имеющее минимальный вес среди ребер, не входящих в 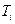и не со­ставляющих циклов с ребрами из .

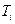Следующая теорема утверждает, что алгоритм Краска­ла всегда приводит к остову минимального веса:

при i < n – 1 граф T_{i+ 1} всегда можно построить. Граф T_{n- 1} будет являться остовом минимального веса в графе (G,w).

Доказательство:

Граф T_i имеет ровно i ребер и потому при i < n – 1 является несвязным. А, так как, граф G связен, то в нем есть по меньшей мере одно ребро, не составляющее циклов с ребрами графа T_i. Итак, нужное ребро U_{i+ 1}существует и граф T_{i+ 1}можно построить.

В качестве иллюстрации рассмотрим взвешенный граф, изображенный на рисунке. 3.18.

Полагаем . Среди оставшихся ребер минимальный вес име­ет, например, ребро 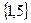. Однако оно не пригодно для построения, поскольку составляет цикл с двумя предыдущими рёбрами. Можно взять .

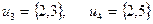Итак, рёбра составляют остов минимального веса. А сам вес остова равен 10.

1 3 5

· ·

1 2 4 4

· · ·

4 5 2 3 3

1 5

· ·

1 2 4

· · ·

4 2 3 3

Рисунок 3.18 – Граф и его остов минимального веса

3.5 Выполнение работы

Каждый студент получает номер задания для написания программы, реализующей конкретную задачу. Инструментарий не ограничивается.

Программа должна предусматривать ввод элементов графа, применение анимации (прорисовку графов) и выдачу результатов.

3.6 Содержание отчета

1. Наименование и цель работы

2. Краткие теоретические сведения

3. Описание программы

4. Схема алгоритма

5. Текст программы

6. Контрольный пример

7. Выводы

3.7 Контрольные вопросы

1. Дать определение графа.

2. Что такое взвешенный и ориентированный граф?

3. Основные шаги алгшоритмов:

- Дейкстры,

- Форда-Фалкерсона,

- Флери,

- транспортной задачи,

- задачи о коммивояжере,

- Краскала.

4. Чем отличается Эйлеров цикл от Гамильтонового?

4 ЛАБОРАТОРНАЯ РАБОТА № 4

Дата добавления: 2015-08-31