Построение ОНК по методике Шеннона-Фано

Построение оптимального кода по методу Шеннона-Фано для ансамбля из M сообщений сводится к следующей процедуре:

1) множество из M сообщений располагают в порядке убывания вероятностей;

2) первоначальный ансамбль кодируемых сигналов разбивают на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны;

3) первой группе присваивают символ 0, второй группе символ 1;

4) каждую из подгрупп делят на две группы так, чтобы их суммарные вероятности были по возможности равны;

5) первым подгруппам каждой из групп вновь присваивают 0, а вторым - 1, в результате чего получают вторые цифры кода. Затем каждую из четырех подгрупп вновь делят на равные (с точки зрения суммарной вероятности) части и т. д. До тех пор, пока в каждой из подгрупп останется по одной букве.

Рассмотрим несколько конкретных примеров построения оптимальных кодов.

Пример: Построим оптимальный код сообщения, состоющего из восьми равновероятных букв.

Решение. Так вероятности данного ансамбля сообщений равны p1 = p2 =... = = p8 = 2-3 и порядок их расположения не играет роли, то расположим их так, как показано в табл. 1. Затем разбиваем данное множество на две равновероятные группы. Первой группе в качестве первого символа кодовых слов присваиваем 0, а второй - 1. Во второй колонке табл. 1 записываем четыре нуля и четыре единицы. После чего разбиваем каждую из групп еще на две равновероятные подгруппы. Затем каждой первой подгруппе присваиваем 0, а второй - 1 и записываем в третью колонку табл. 1. Далее каждую из четырех подгрупп разбиваем на две равновероятные части и первой из них присваиваем 0, а второй - 1. Таким образом в четвертой колонке табл. 1 появится значение третьего символа кодовых слов.

Таблица 4.1 – Оптимальный код равновероятных букв.

Буква	Кодовое слово полученное после разбиения
	первого	Второго	третьего
А1 А2 А3 А4 А5 А6 А7 А8

Проверка оптимальности кода осуществляется путем сравнения энтропии кодируемого (первичного) алфавита со средней длиной кодового слова во вторичном алфавите.

Для рассматриваемого примера энтропия источника сообщений

H = log₂N = log₂8=3 бит/символ

а среднее число двоичных знаков на букву кода

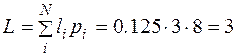
где l_i - длина i -ой кодовой комбинации; p_i - вероятность появления i -го символа комбинации длиной в l_i.

Таким образом, H=L, т. е. код является оптимальным для данного ансамбля сообщений.

Вывод: Для ансамблей равновероятных сообщений оптимальным является равновероятный код. Если число исходных элементов ансамбля равно целой степени двух, то всегда H=L.

Пример: Первичный алфавит состоит из 8 символов со следующими вероятностями появления: a₁=0,5; a₂=0,25; a₃=0,098; a₄=0,052; a₅=0,04; a₆=0,03; a₇=0,019; a₈=0,011. Построить ОНК по методу Шеннона - Фано и подсчитать коэффициенты.

Дата добавления: 2015-08-31