Синтез КБВ с помощью метода эквивалентных схем

При синтезе КБВ на базе решения краевой задачи электродинамики наиболее трудоемким является решение дисперсионного уравнения волновода, частично заполненного обрабатываемой средой.

С помощью метода эквивалентных схем можно существенно ускорить проектирование рабочей камеры и получить общий алгоритм решения задачи синтеза КБВ, собранных на линиях передачи, показанных на рис.5.2.

Поскольку наибольшая неравномерность нагрева может возникнуть вдоль оси волновода КБВ, то для решения задачи синтеза достаточно иметь выражение для погонной мощности потерь 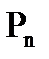, рассчитанное для волн квази-Н₁₀ или квази-Т. Но тогда необходимо знать постоянную распространения этих волн. Наиболее просто получить выражение этой величины с помощью метода эквивалентных схем.

Удобную для расчетов эквивалентную схему линии передачи (рис.5.2) удается построить при распространении в ней волны одного типа, а достоверность результатов расчета параметров линии передачи с помощью этой схемы в значительной степени определяется точностью задания параметров эквивалентной схемы.

Выберем параметры эквивалентной схемы так, чтобы постоянная распространения, найденная из эквивалентной схемы, равнялась постоянной распространения этой же волны, найденной из соответствующего дисперсионного уравнения.

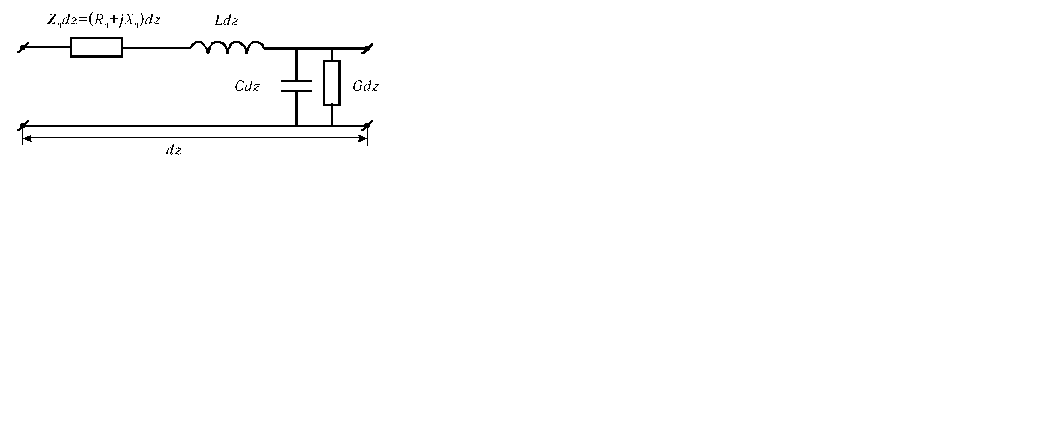
Рисунок 5.2. - Эквивалентная схема бесконечно малого участка волновода,

частично заполненного обрабатываемой средой

Найдем параметры эквивалентной схемы круглого волновода с обрабатываемым стержнем вдоль оси волновода. Для волны типа Е при n = 0 запишем дисперсионное уравнение в виде

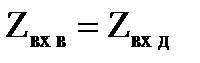(5.1)

где , .

Так как среда с 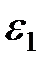бывает обычно без потерь, то 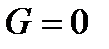. Обмен энергии между воздушным слоем и обрабатываемой средой характеризуется потоком 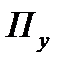, а потому определим погонное сопротивление 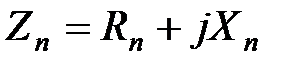, характеризующее влияние обрабатываемой среды на волновые свойства линии, как

, (5.2)

где ; 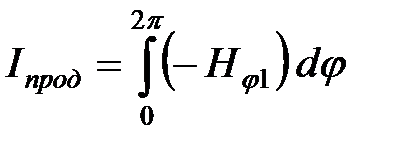, то из (5.13)

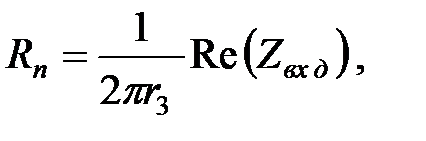(5.3 а)

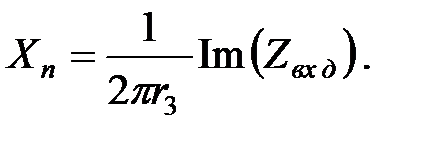(5.3 б)

Из эквивалентной схемы постоянная распределения равна

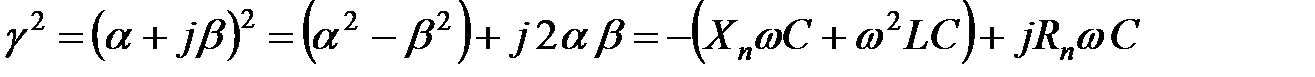, (5.4)

и записывается как

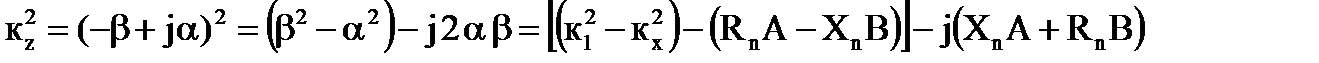; (5.5)

Сравнивая (5.4) и (5.5), получим два уравнения, из которых

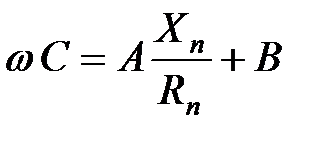, ; (5.6)

где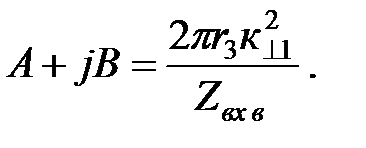

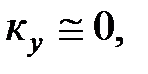
Так как при оптимальной толщине обрабатываемой среды энергия переносится в основном квази - Т волной в воздушном слое, то - входное сопротивление квадрата поверхности обрабатываемой среды при распространении волны по радиусу к оси волновода.

Тогда

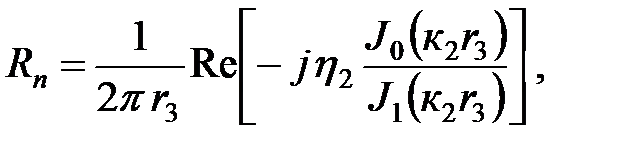(5.7 а)

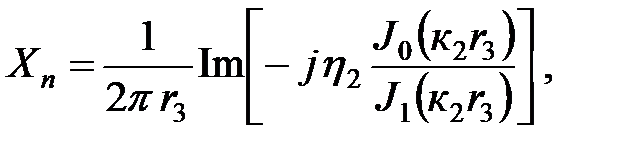(5.7 б)

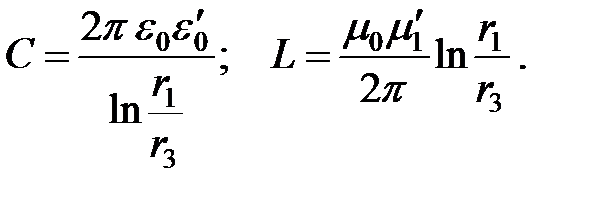(5.7 в)

Зависимости 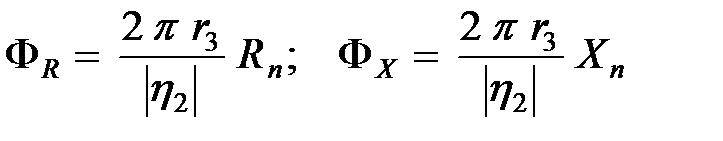от 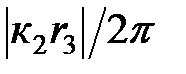приведены на рис.5.4 и рис.5.5.

Соотношения (5.7) тем точнее, чем точнее выполняется условие

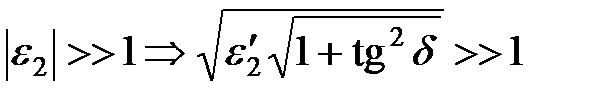, (5.8)

причем, чем больше 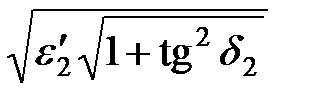, тем точнее эквивалентная схема, вплоть до достаточно толстых слоев обрабатываемого объекта.

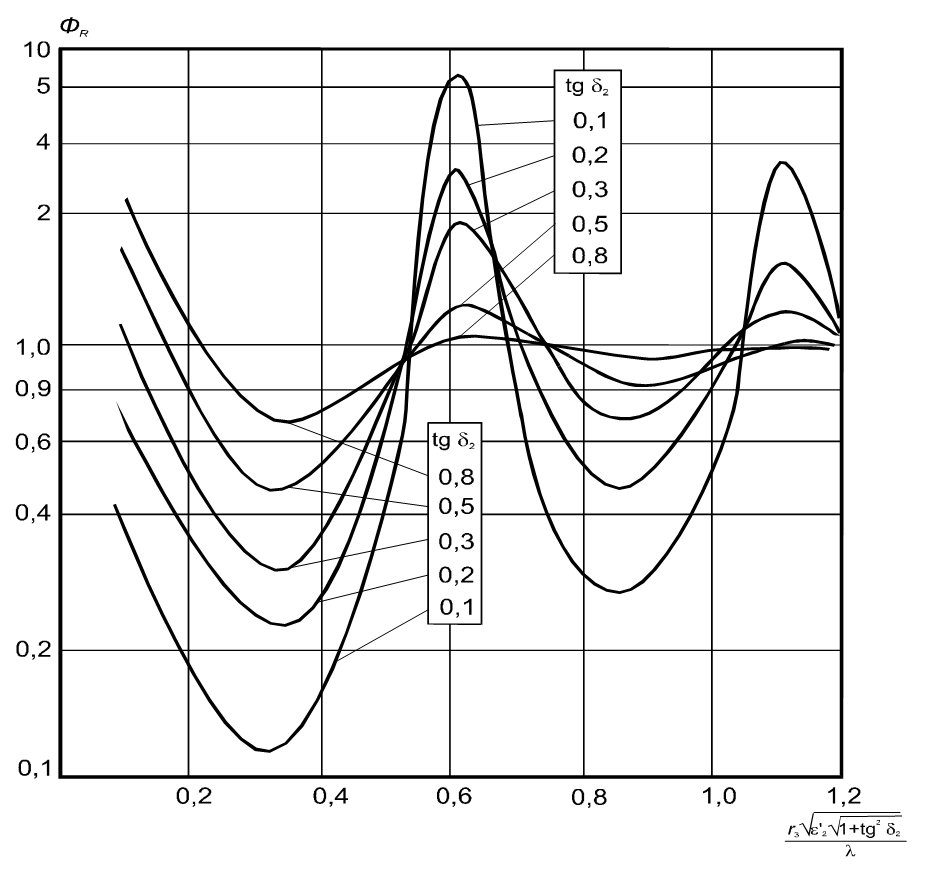
Рисунок 5.4.- Зависимость 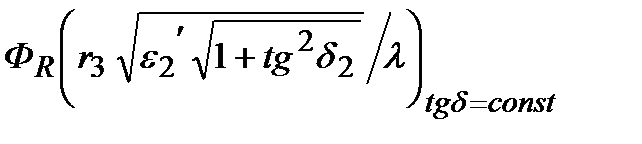для круглого волновода с поглощающим стержнем вдоль оси

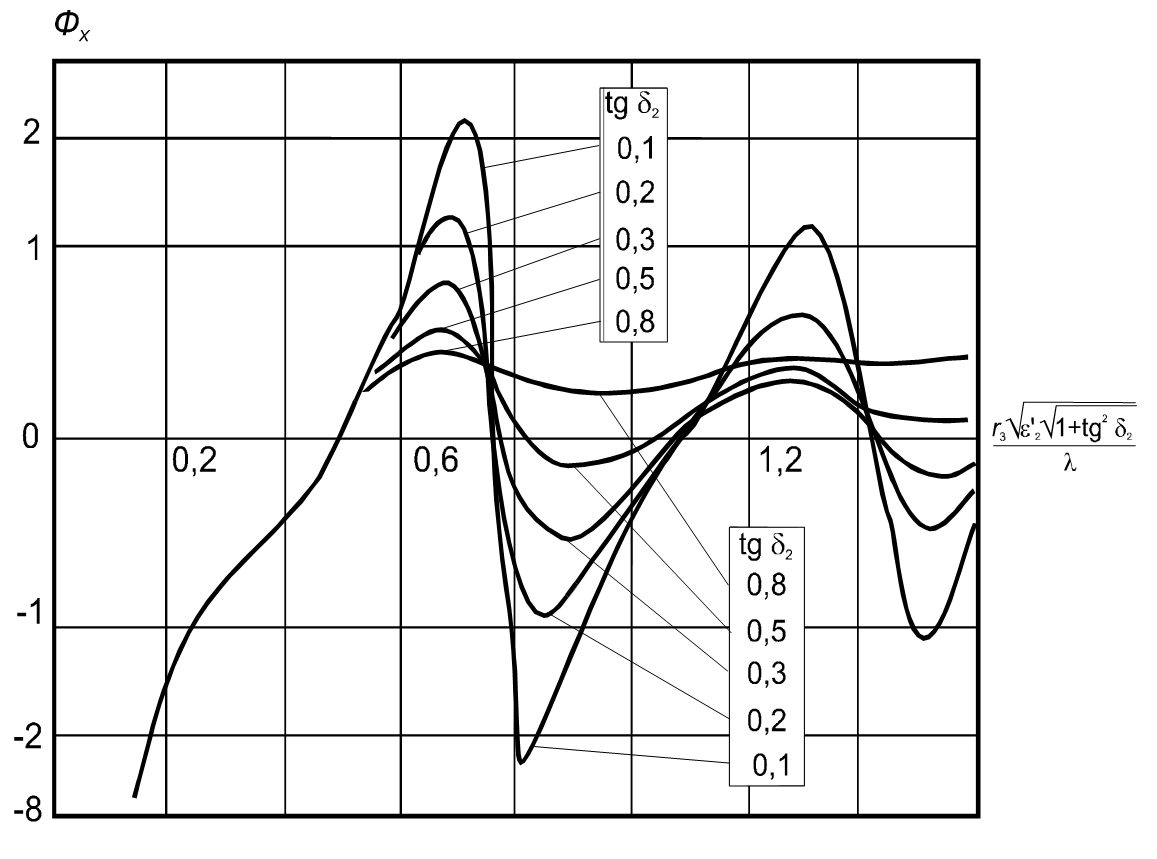
Рисунок 5.5.- Зависимость 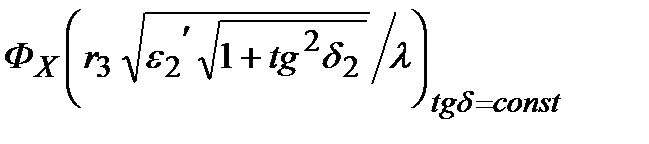для круглого волновода с поглощающим стержнем вдоль оси

Дата добавления: 2015-08-31