Основные понятия, связанные с интерпретацией

Формула A называется истинной при интерпретации I, если A ^{( I )} = 1.

Формула A называется общезначимой или тождественно истинной, если она истинна при любой интерпретации I.

Формула A называется выполнимой, если существует интерпретация, в которой она истинна, в противном случае она называется невыполнимой (или тождественно ложной).

Формула A логически следует из множества формул Γ, если в любой интерпретации, в которой истинны все формулы из множества Γ, истинна также формула A.

Формулы A и B называются логически равносильными, если { A } Þ B и { B } Þ A. Логическую равносильность формул A и B обозначают A ≡ B.

Пусть теперь Γ - множество предложений (Γ Í Sent (σ)), тогда σ -структура, в которой истинны все предложения из Γ, называется моделью множества Γ.

Изоморфизм. Пусть заданы две σ -структуры A и B. Отображение π: U ^A ® U ^B называется изоморфизмом структуры A в структуру B, если

(1) π - взаимно однозначно,

(2) для каждого предикатного n -местного символа P Î s и для любых a ₁, a ₂,..., a_n Î U ^A

(a ₁, a ₂,..., a_n) Î P ^A Û (π(a ₁), π(a ₂),..., π(a_n)) Î P ^B,

(3) для каждого функционального n -местного символа f Î σ и для любых a ₁, a ₂,..., a_n Î U ^A

π (f ^A (a ₁, a ₂,..., a_n)) = f ^B (π(a ₁), π(a ₂),..., π(a_n)).

Две s-структуры A и B называются элементарно эквивалентными, если на них истинны одни и те же s-предложения (сокращенно A ≈ B).

Если универсум конечен, то предикаты и функции на нем можно представить в виде таблиц, графов и других наглядных конструкций. Пусть, например, универсум U состоит из 6 элементов a ₁, a ₂,..., a ₆, и двухместное отношение P на U задано множеством пар P = {(a_i, a_j)| j делит i }; очевидно, P содержит пары (a ₁, a ₁), (a ₂, a ₁), (a ₂, a ₂), (a ₃, a ₁) и т.д.

Отношение P можно представить таблицей (Рис.1), в которой на пересечении i -й строки и j -го столбца находится 1, если i делится на j, и 0 - в противном случае.

Это же отношение можно задать с помощью графа с шестью вершинами, в котором из вершины с номером i в вершину с номером j проведена дуга в том и только том случае, когда (a_i, a_j) Î P.

Подсчитывая все k -местные (k = 0, 1, 2,...) отношения на множестве из n элементов (n = 1, 2,...), получим, что их число равно .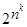

То же для функций. Число к-местных равно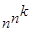

(ν₁, ν₂,..., ν _k; μ₁, μ₂,..., μ _n), тогда число различных структур сигнатуры σ на универсуме из n

элементов равно .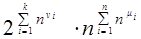

Долей выполнимости предложения A Î L (s) на универсуме U = {1, 2,..., n } называется предел отношения g _n (A) числа структур сигнатуры s на универсуме U_n, в которых истинно предложение A, к числу всех структур сигнатуры s на U_n. Без предела это объем выполнимости.

Закон нуля и единицы: если формула логики 1 порядка не содержит функциональных и нуль-местных предикатных символов, то ее доля выполнимости равно 1 или 0.

Введенное нами определение логического следования не дает непосредственного способа выяснения, следует ли логически та или иная формула из множества формул Γ.

Дата добавления: 2015-08-31