Исключающие кванторы

Формализация доказательства.

1) Множество очевидных утверждений.

2) Правила логического вывода (разветвляющие и не разветвляющие)

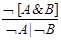
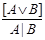
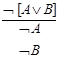
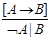
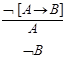
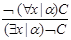
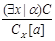
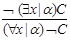
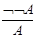
Сказать про исключающие кванторы.

Задача из «Г следует А?» превращается в «из Г и не А следует тождественная ложь»

Пример 1. Выясним, является ли предложение $ z [ S (z) & P (z)] логическим следствием предложений " x [ P (x) → M (x)] и $ y [ S (y) & M (y)]?

1 $ y [ S (y) & M (y)] первая посылка

↓

2 " x [ P (x) → M (x)] вторая посылка

↓

3 $ z [ S (z) & P (z)] отрицание заключения

↓

4 [ S (a) & M (a)] из (1)

↓

5 [ P (a) → M (a)] из (2)

↓

6 (" x|a)[ P (x) → M (x)] из (2)

↓

7 " z [ S (z) & P (z)] из (3)

↓

8 S (a) из (4)

↓

9 M (a) из (4)

______↓___________

↓ ↓

10.1 P (a) 10.2 M (a) из (5)

↓

11.1 [ S (a)& P (a)] из (7)

↓

12.1 (" z|a) [ S (z)& P (z)] из (7)

______↓_______________

↓ ↓

12.1.1 S (a) 12.1.2 P (a) из (11.1)

↓

12.1.3 P (a) из (12.1.2)

Выражения вида (" x | y ₁, y ₂,..., y_k) и ($ x | y ₁, y ₂,..., y_k) будем называть исключающими кванторами общности и существования соответственно.

Истинностные значения этих формул считаем соответственно равными истинностным значениям формул " x [(x ≠ y ₁) & (x ≠ y ₂) &... & (x ≠ y_k) → A ], $ x [(x ≠ y ₁) & (x ≠ y ₂) &... & (x ≠ y_k) & A ].

Формулу будем называть Γ -формулой, если в списке исключений каждого квантора находятся все свободные переменные, расположенные в его области действия.

Заметим, что любая формула A из Form (σ) логически равносильна некоторой Γ -формуле. Чтобы по формуле A построить логически равносильную ей Γ -формулу достаточно воспользоваться соотношениями 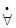x A ≡ (" x | y ₁, y ₂,..., y_k) A & 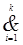A_x [ y_i ], x A ≡ ($ x | y ₁, y ₂,..., y_k) A Ú 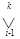A_x [ y_i ],

где y ₁, y ₂,..., y_k - список переменных, совпадающий со списком свободных переменных формулы A, а A_x [ y_i ] - формула, полученная из формулы A заменой свободных вхождений переменной x на y_i.

Пример. Формула " x $ y R (x, y), где R - двухместный предикатный символ, логически равносильна Γ -формуле (" x) [($ y | x) R (x, y)Ú R (x, x)].

Ветвь назовем блокированной, если она содержит некоторую формулу B и ее отрицание B.

Определение поискового дерева для утверждения Γ Þ A дадим с помощью правил его построения.

(П1) Дерево, состоящее из одного узла, помеченного формулой A, и всех формул из Г, является поисковым деревом. Все узлы этого дерева считаем неиспользованным.

(П2) Если в дереве есть неиспользованный узел v, которому приписана формула, являющаяся посылкой одного из правил вывода, то с помощью этого правила каждая неблокированная ветвь W, проходящая через узел v, расширяется следующим образом:

· если правило разветвляющее, то из концевого узла ветви W проводятся две дуги, оканчивающиеся новыми вершинами, которым приписываются формулы-заключения данного правила;

· если правило, соответствующее узлу v, - не разветвляющее, то к концевому узлу ветви W присоединяются последовательно один к другому новые узлы, помеченные формулами-заключениями.

Уточнения требуют случаи применения правил (") и ($), поскольку они связаны с выбором параметра a. При использовании правила (") в качестве a выбирается параметр с наименьшим номером, не входящий в список исключений в посылке данного правила. При использовании правила ($) выбирается параметр с наименьшим номером, не встречающийся в расширяемой ветви, в том числе и в списке α. После расширения дерева считаем узел v использованным, а вновь построенные узлы – неиспользованными.

Очевидно, с помощью правил П1-П3 поисковое дерево для утверждения Γ Þ A определяется неоднозначно. Любую последовательность построенных деревьев будем называть поисковой. Если она бесконечна, то 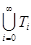также будем называть поисковым деревом.

Лемма (о поисковых последовательностях). Пусть T ₁, T ₂,... - последовательность поисковых деревьев для утверждения Γ Þ A и D_i - множество параметров, используемых в дереве T_i, i = 1, 2,.... Если существует интерпретация I сигнатуры σ на универсуме U, в которой истинны все формулы из множества Γ и формула A, то для каждого i = 1, 2,... существует интерпретация I_i сигнатуры σ È D_i, такая, что в T_i есть ветвь, все формулы которой истинны в интерпретации I_i.

[Если из Г не следует А, то на любом шаге алгоритма существует ветвь дерева и интерпритация, в которой истинны все формулы ветви]

Доказательство. Для i = 1 утверждение леммы очевидно. Пусть существует интерпретация I_{i -1} сигнатуры σ È D_{i -1}, являющаяся расширением интерпретации I, такая, что в T_{i -1} есть ветвь W, все формулы которой истинны в I_{i -1}, и пусть T_i получено из T_{i -1} применением некоторого правила вывода к узлу v.

Если v Ï W, то ветвь W будет искомой ветвью и в дереве T_i. При этом интерпретация символов из множества D_i \ D_{i -1}, если такие есть, может быть произвольной.

Пусть теперь v Î W. Если v имеет вид (" x | α) C, и D_i = D_{i -1}, то формулы, присоединяемые к концевой вершине ветви в соответствии с правилом вывода, будут истинны в интерпретации I_i = I_{i -1}. Если же D_i получено из D_{i -1} добавлением нового параметра a_n, то берем в качестве a_n ^{( I )} произвольный элемент из U, тогда присоединяемые к W формулы C_x [ a_n ] и (" x | α, a_n) C будут истинными в полученной интерпретации I_i.

Пусть теперь v имеет вид ($ x | α) C и при этом D_i получено из D_{i -1} добавлением параметра a_n. Поскольку формула ($ x | α) C истинна в интерпретации I_{i -1}, то существует интерпретация I', совпадающая с I_{i -1} всюду, кроме, возможно, переменной x, такая, что C ^{( I’ )} = 1. Положим a_n ^{( I )} = x ^{( I’ )}, и тогда присоединяемая к W формула C_x [ a_n ] будет истинной в I_i. Рассмотрение остальных способов расширения дерева предоставляем читателю.

Ветвь назовем блокированной, если она содержит некоторую формулу B и ее отрицание B.

Определение поискового дерева для утверждения Γ Þ A дадим с помощью правил его построения.

(П1) Дерево, состоящее из одного узла, помеченного формулой A, и всех формул из Г, является поисковым деревом. Все узлы этого дерева считаем неиспользованным.

(П2) Если в дереве есть неиспользованный узел v, которому приписана формула, являющаяся посылкой одного из правил вывода, то с помощью этого правила каждая неблокированная ветвь W, проходящая через узел v, расширяется следующим образом:

· если правило разветвляющее, то из концевого узла ветви W проводятся две дуги, оканчивающиеся новыми вершинами, которым приписываются формулы-заключения данного правила;

· если правило, соответствующее узлу v, - не разветвляющее, то к концевому узлу ветви W присоединяются последовательно один к другому новые узлы, помеченные формулами-заключениями.

Уточнения требуют случаи применения правил (") и ($), поскольку они связаны с выбором параметра a. При использовании правила (") в качестве a выбирается параметр с наименьшим номером, не входящий в список исключений в посылке данного правила. При использовании правила ($) выбирается параметр с наименьшим номером, не встречающийся в расширяемой ветви, в том числе и в списке α. После расширения дерева считаем узел v использованным, а вновь построенные узлы – неиспользованными.

Очевидно, с помощью правил П1-П3 поисковое дерево для утверждения Γ Þ A определяется неоднозначно. Любую последовательность построенных деревьев будем называть поисковой. Если она бесконечна, то 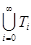также будем называть поисковым деревом.

Если все ветви поискового дерева, построенного для Γ Þ A, блокированы, то такое дерево называется доказательством (в виде дерева) формулы A из посылок (гипотез) Γ.

Если для утверждения Γ Þ A существует дерево-доказательство, то будем говорить, что формула A выводима из множества гипотез Γ, и обозначать Γ |- A.

Теорема (о корректности дедуктики). Если Γ |- A, то Γ Þ A.

Доказательство. Пусть Γ |- A и T - соответствующее дерево-доказательство. Если бы A логически не следовала из Γ, то существовала бы интерпретация I сигнатуры σ, в которой были бы истинны все формулы из множества Γ и формула A. Но тогда по лемме о поисковой последовательности существовала бы ветвь в дереве T, все формулы которой были бы истинны в некотором расширении интерпретации I, что противоречит тому, что в T все ветви блокированы. Теорема доказана.

Ветвь W называется насыщенной относительно множества D' Í D, если:

· вместе с любой посылкой любого разветвляющего правила она содержит хотя бы одну заключительную формулу данного правила,

· вместе с любой посылкой неразветвляющего правила она содержит все заключительные формулы данного правила,

· она содержит каждую формулу из множества Γ.

Уточнения, как и прежде, требуют правила (") и ($). Если формула (" x | α) C принадлежитветви W, то для любого a Î D' формула C_x [ a ] также ей принадлежит; если формула ($x| α) C принадлежит W, то, по крайней мере, для одного a Î D' формула C_x [ a ] принадлежит W.

Поисковое дерево называется полным относительно множества параметров D', если любая его ветвь либо насыщена относительно D', либо блокирована.

Лемма (о существовании полного дерева). Для любого утверждения вида Γ Þ A существует полное поисковое дерево.

Доказательство. Уточним правила построения поисковых деревьев следующим образом. В правиле П2 в качестве v будем выбирать узел минимальной глубины, удовлетворяющий остальным требованиям. Если хотя бы одно из правил П2 и П3 применимо, то обязательно его применяем.

Используя уточненные правила, либо через конечное число шагов получим дерево, в котором каждая ветвь блокирована или насыщена, либо процесс будет продолжаться бесконечно. В последнем случае объединени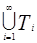е , где 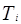- дерево, полученное на i-ом шаге, будет искомым деревом, в котором каждая бесконечная ветвь будет насыщенной, а каждая конечная будет блокированной или насыщенной.

Теорема (о полноте дедуктики). Если Γ Þ A, то Γ |- A.

Доказательство. Пусть формула A не выводима из множества Γ, тогда полное дерево T для утверждения Γ Þ A содержит, по крайней мере, одну неблокированную насыщенную ветвь W. Пусть D' - список параметров, входящих в эту ветвь (он может быть как конечным, так и бесконечным).

Рассмотрим D' в качестве универсума и зададим интерпретацию I сигнатуры σ на D' следующим образом. Для k -местного предикатного символа R Î σ положим

R ^{( I )}={(a ₁, a ₂, …, a _k)| «R (a ₁, a ₂, …, a _k)»Î W }.

Легко доказать индукцией по построению формулы, учитывая правила построения дерева, что при такой интерпретации все формулы, входящие в ветвь W, будут истинными. В том числе будут истинны все формулы из множества Γ и формула Ø A, следовательно, A логически не следует из Γ.

Объединяя теоремы о корректности и полноте, получим следующую теорему.

Теорема (об адекватности дедуктики). Γ Þ A тогда и только тогда, когда Γ |- A.

Теорема (о компактности). Если Γ Þ A, то существует конечное подмножество Γ' Í Γ такое, что Γ' Þ A.

Действительно, пусть Γ Þ A, тогда по теореме о полноте Γ |- A, следовательно, существует дерево-доказательство, в котором все ветви блокированы и, следовательно, конечны. Следовательно, число гипотез из Γ, содержащихся на этих ветвях, конечно, они и образуют требуемое конечное подмножество гипотез.

Дата добавления: 2015-08-31