Прямолінійна кореляція

Основні розрахункові теми 3-го розділу

Явища та процеси, які відбуваються в суспільстві, зокрема у сфері правової діяльності, взаємопов'язані і взаємообумовлені. Ці взаємо­зв'язки статистика вивчає, використовуючи кореляційно-регресійний аналіз.

В основі цього аналізу лежить припущення про те, що залежність між значеннями факторної ознаки та умовни­ми середніми значеннями результативної оцінки може бути представ­лена у вигляді функції:

Y=f(x),

яка називається рівнянням регресії. Розраховані за цим рівнянням очікувані середні значення результативної ознаки для кожної (із рів­нів) факторної ознаки х позначаються у і називаються теоретични­ми, на відміну від емпіричних, тобто одержаних у результаті безпосередніх спостережень за значенням у.

Якщо аналітичне групування дає змогу виявити тільки наявність та напрям зв'язку, то за допомогою рівняння регресії можна вста­новити, наскільки в середньому зміниться значення результативної ознаки при зміні факторної на одну одиницю.

Обчислення, пов'язані з використанням кореляційно-регресійного аналізу зв'язку двох ознак, що характеризують ту чи іншу сферу пра­вової діяльності, доцільно розділити на такі етапи:

• вибір форми рівняння регресії;

• розрахунок параметрів рівняння регресії;

• оцінка щільності зв'язку;

• перевірка суттєвості зв'язку.

З метою вибору форми рівняння регресії у статистиці ко­ристуються такими прийомами.

Теоретичний аналіз базується на професійних знаннях дослідника про досліджуваний зв'язок. Щоб правильно застосувати кореляцій­ний метод, необхідно глибоко розуміти сутність процесів взаємозв'язків. Важливо пам'ятати, що кореляційні методи не виявляють причин зв'язків між тими чи іншими явищами, характер їх взаємодії, тобто не встановлюють причин залежності, їх роль зводиться до встановлен­ня кількісної закономірності між досліджуваними ознаками і суціль­ністю зв'язку.

Але перш ніж визначити кількісну залежність досліджуваних ознак, необхідно встановити, який із досліджуваних показників є факторним, а який — результативним. Наприклад, якщо передбачається досліди­ти рівень злочинності в регіоні у зв'язку з чисельністю населення, то першочергово виявляється можливість цього зв'язку, виходячи з ре­альної дійсності, а потім допускається, що факторним показником є чисельність населення, а результативним — рівень злочинності.

У ході теоретичного аналізу показників необ­хідно врахувати діапазон можливих значень факторної ознаки. Якщо в досліджуваній сукупності факторна ознака змінюється у вузьких рамках, то в полі її фактичної варіації відрізок кривої може бути наближений лінійним рівнянням.

Запас функцій, які можуть бути використані для побудови регре­сії, досить обмежений. Для цього варто використовувати функції, лінійні щодо параметрів.

Розглянемо функцію, яку застосовують в ході аналізу право­вої діяльності частіше за інші:

лінійна — Y = а + b х

Параметр а лінійного рівняння регресії — це значення у при х = 0. Якщо нуль перебуває в рамках фактичної варіації ознаки х, то а — одне із теоретичних значень у, якщо х у досліджуваній сукупності не приймає значень, близьких до 0, то параметр а не має реального змісту.

Параметр b називається коефіцієнтом регресії і показує, на скіль­ки одиниць в середньому зміниться у при зміні х - на одиницю.

Параметри рівняння регресії обчислюють способом найменших квадратів. Основна умова цього методу полягає в тому, що сума квадратів відхилень теоретичних значеньY від емпіричних повинна бути мінімальною:

Σ (Y – y)² = min

Параметри рівняння регресії, які відповідають цій умові, розраховують шляхом рішення системи нормальних рівнянь. Ця система, наприклад, для лінійної функції (при обчисленні за незгрупованими даними) має такий вигляд:

Σy = na + bΣx

Σxy = aΣx + bΣx².

Розв'язавши систему, одержуємо:

.

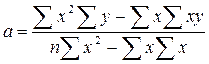
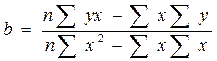Розрахунок рівняння регресії може вестися безпосередньо за пер­винними незгрупованими даними, тому кореляційно-регресійний аналіз правової діяльності повніше використовує інформацію про досліджувані зв'язки, ніж метод групування. Але для розрахунку рівняння регресії необхідно, щоб обидві ознаки були кількісними (в ана­літичному групуванні групувальна ознака може бути якісною).

Використовуючи дані проектного завдання, розрахуємо основні показники, які характеризують тісноту зв’язку між урожайністю зернових культур та якістю ґрунту.

6. Розрахункові данні для кореляційного аналізу

№п.п	Урожайність зернових культур, ц.га У	Якість ґрунту, балів Х	Розрахункові величини	(Yx- Yc)^2
У^2	Y*X	X^2	Yx
						27,85	14,82
						19,912	16,71
						28,732	22,39
						20,794	10,28
						26,086	4,35
						26,086	4,35
						32,26	68,23
						16,384
						23,44	0,31
						17,266	45,35
						28,732	22,39
						20,794	10,28
						29,614	31,52
						21,676	5,4
						26,968	8,81
						26,086	4,35
						33,142	83,58
						15,502	72,22
						22,558	2,08
						16,384
сума						480,266	543,42
середнє		74,65	608,5	1822,4	5607,55	24,013	27,171

Використовуючи данні таблиці та теоретичну частину, викладену вище, розрахуємо коефіцієнти регресії:

= ;

= .

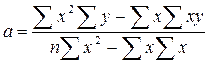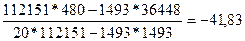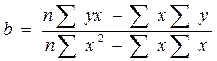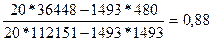Розрахувавши коефіцієнти регресії, ми отримуємо кореляційне рівняння, яке має вигляд: Y = -41,83 + 0,88 х. З цього можемо зробити наступний висновок – із зростанням якості ґрунту на 1 бал урожайність зернових культур у даній сукупності у даній сукупності зростає на 0,88 ц.га.

Наступним кроком кореляційного аналізу є розрахунок показників, які характеризують тісноту зв’язку (коефіцієнт та індекс кореляції):

r = = ;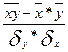

= ;

= ;

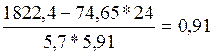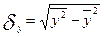і = = .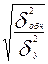

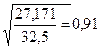Розрахувавши індекс та коефіцієнт кореляції можемо зробити висновок, що зв’язок між досліджуваними ознаками є тісний.

На завершення кореляційного аналізу ми можемо визначити, наскільки відсотків результативна ознака залежить від факторної. Це можливо зробити за допомогою коефіцієнта детермінації:

D = r² * 100% = 0,91² *100 = 83%.

Отже, у цій сукупності рівень урожайності зернових культур залежить від якості грунту на 83%, а решта 17% – це інші фактори впливу, які не увійшли до нашої моделі.

Дата добавления: 2015-08-31