Им. Н.Э. БАУМАНА

Т

треугольник прямоугольник квадрат

ПРЯМАЯ. ОТРЕЗОК. ЛУЧ

две точки могут быть концами единственного отрезка;

через две точки можно провести единственную прямую;

две прямые могут пересекаться только в одной точке.

■ отрезок — все точки прямой, расположенные между какими-либо двумя точками этой прямой, и сами эти две точки;

■ луч — все точки прямой, расположенные по одну сторону от какой-либо точки этой прямой и сама эта точка?

СРАВНЕНИЕ ОТРЕЗКОВ. ДЛИНА ОТРЕЗКА

Отрезки равны, если при наложении их можно совместить.

Отрезки равны, если они имеют одинаковую длину.

ЛОМАНАЯ

Точки А, В, С и D называют вершинами ломаной, а отрезки АВ, ВС и CD — ее звеньями.

КООРДИНАТНЫЙ ЛУЧ

На луче, начало которого является началом отсчета и указан единичный отрезок, для любого числа можно указать соответствующую ему точку, поскольку луч можно продолжить бесконечно. Такой луч называют координатным, а число, которое соответствует точке координатного луча, называют координатой этой точки.

ОКРУГЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ

При округлении числа до некоторого разряда все цифры последующих разрядов заменяются нулями.

Цифра разряда, до которого выполняется округление, остается без изменения, если в округляемом числе за ней следует одна из цифр: 0, 1, 2 3, 4. В остальных случаях к ней прибавляется 1.

Округление часто используется при устных вычислениях. Если один или все компоненты действий близки к круглым числам, то сначала выполняется округление, и действия производятся над круглыми числами, а затем вносится поправка.

ПРИКИДКА РЕЗУЛЬТАТА ДЕЙСТВИЯ

В тех случаях, когда не требуется знать точное значение числового выражения, его компоненты округляют и выполняют действия с I их приближенными значениями. Такую операцию называют прикидкой результата действия.

ВЫЧИСЛЕНИЯ С МНОГОЗНАЧНЫМИ ЧИСЛАМИ

При сложении и вычитании многозначные числа записывают в столбик так, чтобы цифры одноименных разрядов были записаны друг под другом.

ПРЯМОУГОЛЬНИК

Чтобы измерить площадь, надо выбрать единицу (меру) площади. За единицу площади принимают площадь квадрата со стороной, равной единице длины. Площадь фигуры — это число, которое показывает, сколько мер площади — квадратов со стороной, равной единице длины, — можно уложить внутри этой фигуры.

Фигуры равны, если при наложении их можно полностью совместить.

ФОРМУЛЫ

Площадь прямоугольника равна произведению длин его сторон	S = а • Ь
Периметр прямоугольника равен сумме длин его сторон	Р = а + а + Ъ + Ъ, или Р = 2(а + Ъ)
Пройденный путь — это произведение скорости на время движения	s = v • t

Каждое равенство в таблице — это правило вычисления той или

иной величины, записанное на математическом языке. Такие равенства, которые представляют собой запись правила вычисления значения какой-либо величины, называют формулами.

ЗАКОНЫ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ

Законы сложения	Равенство	^т Словесная форма
Переместительный	а + Ь — b + а	От перемены мест слагаемых сумма не меняется
Сочетательный	(а + Ь) + с — = а + (Ь + с)	Если к сумме двух слагаемых прибавить третье слагаемое, то получится то же число, что и от прибавления к первому слагаемому суммы второго и третьего слагаемых

Это равенство иллюстрирует следующее свойство: при умножении числа на сумму можно умножить это число на каждое слагаемое и полученные результаты сложить.

Можно это свойство сформулировать и по-другому: сумму двух или нескольких произведений, содержащих одинаковый множитель, можно заменить произведением этого множителя на сумму остальных множителей.

Это свойство еще один закон арифметических действий — распределительный. Как видим, словесная формулировка этого закона очень громоздкая, и математический язык — это то средство, которое делает ее краткой и понятной:

УРАВНЕНИЯ

Если мы захотим таким же способом решить остальные уравнения, то придем к необходимости деления на нуль. Но на нуль делить нельзя. В самом деле, рассмотрим третье уравнение: у * 0 = 15. Результат деления 15 на 0 должен быть числом, произведение которого на О равно 15. Но произведение любого числа на нуль равно нулю. Значит, такого числа не существует, а деление на нуль не имеет смысла.

на 0 делить нельзя!

УПРОЩЕНИЕ ВЫРАЖЕНИЙ

Рассмотрим выражение Зу. Это произведение числа 3 и буквы у. Говорят, что число 3 — это числовой множитель, а буква у — буквенный множитель. Числовой множитель в таких выражениях обычно называют коэффициентом. Так, в выражении Зу число 3 — коэффициент при у. Упрощая выражение 2х + 3jc, мы сложили коэффициенты 2 и 3,буквенный множитель х оставили без изменения.

МАТЕМАТИЧЕСКИЙ ЯЗЫК

Чтение выражения начинается с последнего выполняемого действия.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Выражение, полученное в процессе решения, — это математическая модель реальной жизненной ситуации, о которой говорится в задаче. В первой задаче рассматривается встречное движение, во второй — совместная работа, и обе эти ситуации описываются одинаковыми математическими моделями.

ДЕЛЕНИЕ С ОСТАТКОМ

Компоненты деления в левой части равенства называют так же как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, j которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка или нацело.

ОБЫКНОВЕННЫЕ ДРОБИ

Дробь как результат деления натуральных чисел

дробь “ читается так: одна третья;

число, стоящее над чертой дроби, — это числитель;

число, стоящее под чертой дроби, — это знаменатель.

ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ

чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть; чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ. СМЕШАННЫЕ ЧИСЛА

5:3 = 1 2\3 (читается: «одна целая две третьих»). Такие числа называются смешанными: 1 — целая часть, а 2\3 дробная часть.

ОКРУЖНОСТЬ И КРУГ

B A

Радиус

диаметр C

N M

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменения. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить без изменения.

УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННОЙ ДРОБИ НА НАТУРАЛЬНОЕ ЧИСЛО

Чтобы умножить обыкновенную дробь на натуральное число, надо ее числитель умножить на это число.

Если числитель дроби — делится на натуральное число n, то, чтобы разделить эту дробь на n, надо ее числитель разделить на это число: a\b:n=a:n\b

Если числитель дроби — не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо ее знаменатель умножить на это число: a\b:n=a\bn

ОПРЕДЕЛЕНИЕ УГЛА. РАЗВЕРНУТЫЙ УГОЛ

Угол — это фигура, образованная двумя лучами, имеющими общее начало.

Развернутый угол — это угол, образованный дополнительными лучами.

A СРАВНЕНИЕ УГЛОВ НАЛОЖЕНИЕМ

M

N B K C

На рисунке показано, как попытались совместить углы ABC и MNK, но это оказалось невозможным. Понятно, что эти углы не равны. Заметим, что угол MNK целиком оказался внутри угла ABC. Поэтому естественно считать, что угол MNK меньше угла ABC: ZMNK< Z.ABC.

Измерение углов

транспортир

Острым углом называют угол, величина которого меньше 90. Тупым углом называют угол, величина которого больше 90, но меньше 180.

Биссектриса угла

Биссектриса - луч с началом в вершине угла, делящий угол на два равных угла.

ТРЕУГОЛЬНИК

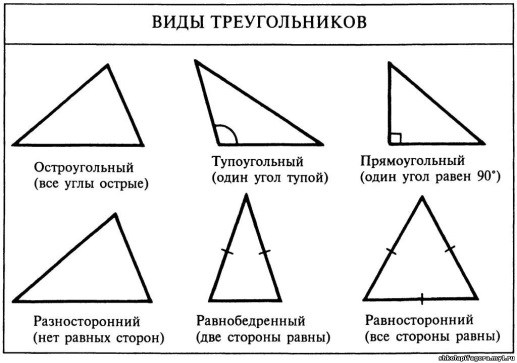Сторона треугольника

Всегда меньше

Суммы двух

Других его сторон.
Площадь треугольника

Чтобы найти площадь треугольника, разобьем его на два прямоугольных треугольника. Для этого из точки В проведем к стороне АС под прямым углом отрезок BD.

Площадь треугольника можно найти по формуле

S = (а ♦ К): 2

S = (а ♦ К): 2. Сумма углов треугольника равна 180°.

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ. МАСШТАБ

Одна единица измерения на схеме соответствует двум тысячам таких же единиц в действительности. Например, если на схеме отрезок имеет длину 1 см, это значит, что на I самом деле длина этого отрезка — 2000 см, или 20 м. Кратчайшее расстояние между двумя точками — это длина отрезка прямой, соединяющего эти точки.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ. ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ

Значок -L заменяет слово перпендикуляр, а запись АВ±а заменяет предложение: «Отрезок АВ перпендикулярен прямой а».

Расстояние от точки до прямой равно длине перпендикуляра, проведенного из этой точки к данной прямой.

Две прямые называют взаимно перпендикулярными, если они пересекаются под прямым углом.

СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР

Точки серединного перпендикуляра к отрезку равноудалены от его концов.

А СВОЙСТВО БИССЕКТРИСЫ УГЛА

В О

y ZXYueG1sTI/NTsMwEITvSLyDtUhcqtYh/QshToUqcYED0PIATrIkEfY6xG7qvj3LCY6jGc18U+yi NWLC0feOFNwtEhBItWt6ahV8HJ/mGQgfNDXaOEIFF/SwK6+vCp037kzvOB1CK7iEfK4VdCEMuZS+ 7tBqv3ADEnufbrQ6sBxb2Yz6zOXWyDRJNtLqnnih0wPuO6y/Dier4Pn1bXZJ42b2vV1X+zhlJr54 o9TtTXx8ABEwhr8w/OIzOpTMVLkTNV4Y1vfLNUcVpCv+xAGe24KoFCyzFciykP8flD8AAAD//wMA UEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5 cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3Jl bHMvLnJlbHNQSwECLQAUAAYACAAAACEA1PuHWPMBAADpAwAADgAAAAAAAAAAAAAAAAAuAgAAZHJz L2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAEErE5t4AAAAJAQAADwAAAAAAAAAAAAAAAABNBAAA ZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAFgFAAAAAA== " strokecolor="black [3040]"/>

С

Точка биссектрисы угла равноудалена от ее сторон. То есть, если ты из одной точки на биссектрисе проведешь перпендикуляры к сторонам, то они будут равны.

ПОНЯТИЕ ДЕСЯТИЧНОЙ ДРОБИ. ЧТЕНИЕ И ЗАПИСЬ ДЕСЯТИЧНЫХ ДРОБЕЙ

Если в десятичной записи числа использована запятая (или точка), то говорят, что число записано в виде десятичной дроби. Для краткости числа, записанные в таком виде, называют просто десятичными дробями. Заметим, что десятичная дробь — это не новый тип числа, а новый способ записи числа.

УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ НА 10, 100, 1000 и т. д.

Правила умножения и деления десятичной дроби на 10, 100, 1000 и т. д. можно сформулировать так: чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо запятую перенести вправо на 1, 2, 3 и т. д. цифры. А если цифр не хватает, приписать справа нули: чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо запятую перенести влево на 1, 2, 3 и т. д. цифры, а если цифр не хватает, приписать слева нули.

СРАВНЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

При округлении десятичной дроби до разряда единиц, десятых, сотых и т. д. все цифры последующих разрядов отбрасываются. При округлении десятичной дроби до разряда, старшего разряда единиц, цифры последующих разрядов целой части числа заменяются нулями, цифры дробной части — отбрасываются. Цифра разряда, до которого выполняется округление, остается без изменения, если в округляемом числе за ней следовала одна из цифр: 0,1,2, 3, 4. В остальных случаях к ней прибавляется 1.

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

Сложение десятичных дробей, так же как и сложение натуральных чисел, выполняется поразрядно. Если вычисления трудно выполнить устно, слагаемые записывают в столбик таким образом, чтобы цифры, стоящие в одноименных разрядах, оказались друг под другом; при этом запятая должна оказаться под запятой, что поможет избежать ошибки при записи.

Умножение десятичных дробей

При умножении десятичных дробей сначала надо выполнить умножение, не обращая внимания на запятую, а затем в произведении отделить запятой справа столько знаков, сколько их имеется после запятой в обоих множителях вместе.

Числа, произведение которых равно 1, называют взаимно-обратными числами.

Степень числа

Значение выражения а² равно площади квадрата со стороной, равной а. Поэтому выражения такого вида принято читать так: «а в квадрате» — или просто: «а квадрат». Например: З² — три в квадрате, 5² — пять в квадрате. Вы знаете, что «квадратный метр», «квадратный сантиметр» обозначаются соответственно м², см². Теперь, когда вы знаете, что такое степень, становится понятным, откуда взялось такое обозначение.

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ. ДЕЛЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ НА НАТУРАЛЬНОЕ ЧИСЛО

Средним арифметическим чисел называют сумму этих чисел, деленную на число слагаемых. А теперь попробуем выполнить деление в столбик, ведь десятичная дробь — это число, записанное в десятичной системе счисления позиционным способом, поэтому деление в столбик выполняется по тем же правилам, что и деление натуральных чисел.

Деление десятичной дроби на десятичную дробь

Деление на десятичную дробь заменяется делением на натуральное число. Для этого нужно и в делимом, и в делителе перенести запятую на столько знаков вправо, сколько их содержится после запятой в делителе, а затем выполнить деление на натуральное число. Если в делимом не хватает знаков, то справа приписывают нули.

Сотая часть числа. Десятая часть числа. Пятая часть числа. Четвертая часть числа.

1% 10% 20% 25%

Половина. Три четверти числа. Треть числа.

50% 75% 33,3%

ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД

А)

Б)

На первом рисунке изображены тела, поверхность которых составлена из плоских фигур — многоугольников. Эти многоугольники называются гранями, а сами тела — многогранниками. На втором рисунке тела ограничены не только плоскими поверхностями. Это круглые тела: цилиндр, конус и шар.

РАЗВЕРТКА ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА

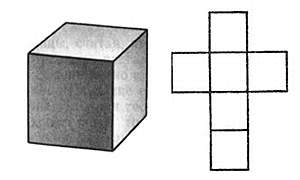
Объём прямоугольного параллелепипеда

Длина - это число, которое показывает, сколько раз отрезок, длина которого принята за единицу (меру), длины, укладывается в отрезке.

Площадь - это число, которое показывает, сколько квадратов со стороной, равной единицы длины (мер площади), можно уложить внутри фигуры.

Объем - это число, которое показывает, сколько кубиков с ребром, равным единице длины (мер объема), можно уложить внутри фигуры.

ДОСТОВЕРНЫЕ, НЕВОЗМОЖНЫЕ И СЛУЧАЙНЫЕ СОБЫТИЯ

Событие, которое в данном опыте обязательно наступит, называют достоверным событием.

Событие, которое в данном опыте наступить не может, называют невозможным событием.

Событие, которое в данном опыте может наступить, а может и не наступить, называют случайным событием.

КОМБИНАТОРНЫЕ ЗАДАЧИ

Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов — белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны — свой флаг?

Решение. Будем рассуждать так. Предположим, что первая полоса (верхняя) белого цвета (Б). Тогда вторая (средняя) полоса, может быть, синей (С) или красной (К), а третья (нижняя) полоса, соответственно, красной (К) или синей (С). Получилось два варианта (две комбинации) цвета полос: белая, синяя, красная (БСК) или белая, красная, синяя (БКС).

Пусть теперь первая полоса синего цвета (С). Тогда вторая полоса может быть белой (Б) или красной (К), а третья полоса, соответственно, красной (К) или белой (Б). Получилось два варианта: синяя, белая, красная (СБК) или синяя, красная, белая (СКВ).

Пусть, наконец, первая полоса красного цвета (К).

Тогда вторая полоса может быть белой (Б) или синей (С), а третья полоса, соответственно, синей (С) или белой (Б).

Получилось два варианта: красная, белая, синяя (КБС) или красная, синяя, белая (КСБ).

Таким образом, всего получилось 6 комбинаций.

Работа Шингирей Дарьяны

Школа №24

6В класс

Дата добавления: 2015-08-31